Лабораторная работа 2 Вариант 2ав Преподаватель Перл Ольга Вячеславовна Геллер Л. А. Группа Р3230

Название	Лабораторная работа 2 Вариант 2ав Преподаватель Перл Ольга Вячеславовна Геллер Л. А. Группа Р3230
Дата	15.10.2022
Размер	56.11 Kb.
Формат файла
Имя файла	lab2.docx
Тип	Лабораторная работа #735279

УНИВЕРСИТЕТ ИТМО

Факультет программной
инженерии и компьютерной техники
Вычислительная математика

Лабораторная работа № 2

Вариант 2ав

Преподаватель: Перл Ольга Вячеславовна Выполнил: Геллер Л. А.

Группа: Р3230

Санкт-Петербург, 2021

Описание метода, расчетные формулы

Решение нелинейных уравнений

• Метод деления пополам

Дано уравнение Г(х) = 0, функция Г(х) непрерывна на [а, Ь], Г(а)*Г(Ь) < 0
Поделим отрезок [а, Ь] пополам; Если / (“+“) = 0, то корень уравнения найден
В противном случае продолжаем рассматривать ту из половин отрезка, на концах которой сохранились разные знаки и повторяем пункты 2), 3)
Итерации продолжаем, пока значение функции не станет меньше по модулю, чем е - небольшое положительное число - точность, заданная на входе

• Метод касательных

1)

2)

Дано уравнение Г(х) = 0, функция Г(х) непрерывна на [а, Ь], Г(а)*Г(Ь) < 0 Построим касательную к Г(х), за следующее приближение х принимается точка

пересечения касательной с Ох : Х ₁ = Х_к

Г ( Хк)

Р'(Хк)^,

3)

Вычисления (п.2) продолжаем, пока \Р(не станет < е - точности, или пока не

выполняется Х_м — Х <8

• Метод простых итераций

1) Дана система, преобразуемая к виду:

Х = /1 (^Х1,^x2^,....^,^Хп ⁾

Х = Л( ^x2^,....^,^Хп ⁾

^Хп = /п ⁽^Х1> ^Х ,...., ^Хп ⁾

, причем функции определены и непрерывны вместе со своими частными производными в некоторой области ^, которой принадлежит точное решение рассматриваемой системы

Выберем начальное приближение X⁰ = (х°, Х⁰,..., Х°)
Подставим в уравнения (п.2) значения из X⁰, таким образом получив новое приближение решений системы
Повторяем пункт 3, пока не выполнится: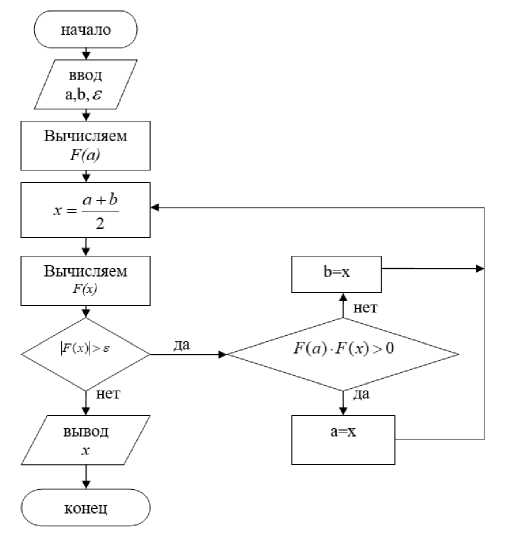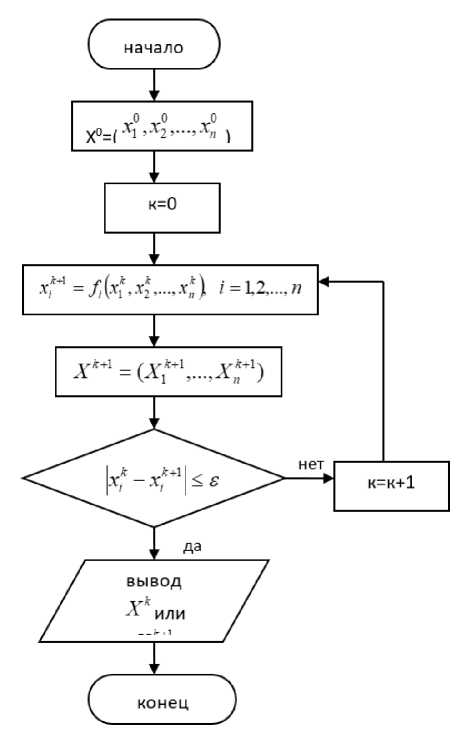

Блок-схема численного метода

• Метод деления пополам

• Метод простых итераций (для систем)

Метод касательных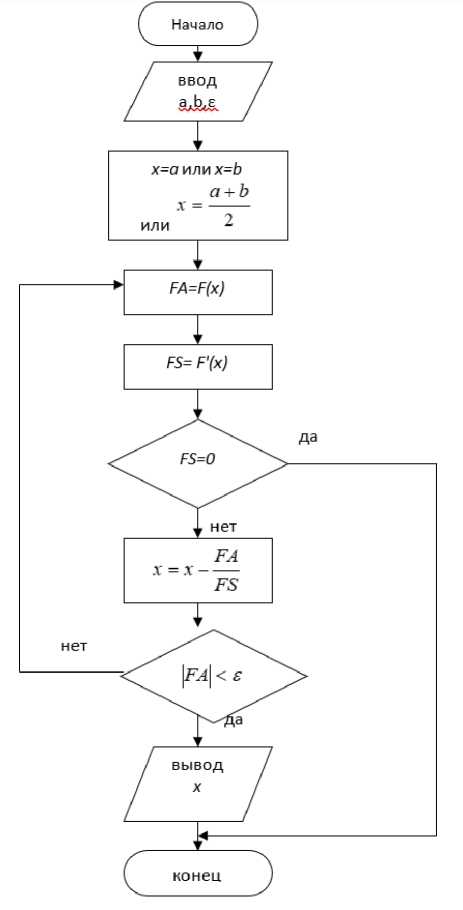

Листинг реализованного численного метода программы

Метод бисекций:

риЬИс уо11 зо!уе() {

ехесИте = 5уз1ет. папоИтеС);

уА = едиаМоп. де1:Еипс() .арр1_у(а);

ИегаЕаопз = О;

С1О {

11:ера1:1оп5++;

х = (а + Ь) /2;

уХ = ециаНоп. деЕЕипс (). арр!у (х);

1Т (уА * уХ > О) а = х;

е!зе Ь = х;

} иЫ1е (МаЕИ .аЬз(уХ) > ер511оп); ехесИте = (ЗузЕепп .папоПте () - ехесТ1те)/1000;

}

Метод касательных:

рцЫ_1с уоН 501уеС ±Е1гошб ЕЧ11а1: 1опЕхсер±1оп {

ехесИте = Зуз’Еет.сцггепЕПтеМИИзС) ;

0оиЫеРипсЕ1оп<0оцЫ.е> Е0ег1уе = с!ег1Уе (еяиаМоп. деЕЕипс О);

х = (а+Ь)/2;

йоцЫе уХ;

йоцОГе IX - Т0ег1уе.арр1у(х);

с1о{

1±ега1:1опз++;

1Т ССХ = = 1:11рош пей» ЕдцаИопЕхсерИопСПроизводная = 9");

уХ = едиаЕтоп.деЕЕипс().аррЪу(х);

их = Е0ер1уе.аррТ.у(х);

х -= (уХ/йХ);

1Л|И11е(Ма'1Р.ай5[уХ) >= ерзИап);

ехесИте = Зуз1ет.сиггеп1ИтеМ11Из() - ехесИте;

Метод простых итераций:

риЬИс уо1й зо1уе() 1Г1Р0Ш5 ЕдиаНопЕхсерНоп {

йр ■{

ИепаИоп5++;

ргеудоцзУагз = Аггауз.соруО/(уагз, уагз.1епд1:11) ; уарз[0] = зоЕ.деЕЕипсз().де!(О).аррТу(рреудоцзУаре[1]); уагз[1] = зоТ. деЕЕцпсз (). де! (1). арр1_у (ргеу1оизУагв [0]);

1Е (Аггаув.зГреатСуарз) .апуМаЕсИСх -> пеш ОаиЫе(х). 1з1пЕ1п11:е() || пет ОоиЫе (х). 180аМ ())) ЕРгош пет ЕциаИопЕхсерИоп("Метод простых итераций не сходятся");

} шРИе (! ХзСопуердей (рреудоизУарз, уагз));

рг!уа1е Ьоо1еап дзСопуегдес!(йоцЫе[] ргеУ1оцзХ, 0оцЫе[] х){

1П1: п = рреудоцзХ.ЕепдЕП;

Еог(1п1 1=0; 1<п; 1++Н

1Е(Ма1:П.аЬ5(х[1] - рреу1оизХ[1]) > ере){ реЕигп ЕаТзе; }

}

реЕигп 1гие;

Примеры и результаты работы программы на разных данных

1) Решение нелинейного уравнения методами биекций и касательных

Решить уравнение или систему уравнений?

1: Решить уравнение

2: Решить систему уравнений

1

Выберите тип решаемого уравнения:

1: Степенное

2: Логарифмическое

3: Тригонометрическое

1

Выберите степенное уравнение:

1: 2^Л(х+1) + 2^л(х-1) + 2^лх - 28 = 0

2: хЛ2 - 8х + 12 = 0

3: хлз - 4хЛ2 + 2х - 8 = 0

2

Введите левую границу отрезка поиска корней:

3

Введите правую границу отрезка поиска корней:

7

Введите точность:

0,0001

Корень, найденный с помощью метода касательных:

х = 5.9999999999999885 +- 1.0Е-4

Решение найдено за 5 итераций.

Время выполнения = 3.0 мс

Корень, найденный с помощью метода бисекций:

х = 6.0 +- 1.0Е-4

Решение найдено за 2 итераций.

Время выполнения = 29.0 мкс

2) Решение системы нелинейных уравнений методом простых итераций

Решить уравнение или систему уравнений?

1: Решить уравнение

2: Решить систему уравнений

2

Выберите систему уравнений:

1: у = хЛ2

х = (уЛ2)/4

2: у = хЛ2 - 2

у = 2Лх

3: х + у = 0.5

у + соз(х) = 0.5

3

Введите точность:

0,0001

х: 0.7390495805952085 +- 1.0Е-4

у: -0.23913017652967106 +- 1.0Е-4

Решение найдено за: 45 итераций

Вывод

Метод Бисекций является самым простым методом решения нелинейных уравнений. Методы Хорд и Касательных являются модификацией метода Бисекций. Они быстрее, но требуют более сложных вычислений (метод касательных также требует ввод начального приближения и поиск производной на каждой итерации). Вышеперечисленные методы обязательно сходятся, если найден отрезок, значения функции на концах которого обладают противоположными знаками (что гарантирует наличие на нем хотя бы одного корня).

Метод Ньютона обладает более высокой сходимостью, чем метод простых итераций за счет использования Якобиана (матрица частных производных), в результате чего повышается сложность вычислений.