рэс. Лабораторная работа 3 Генерирование коррелированных случайных процессов Бригада 5 Выполнили ст гр. 913 Яковлев Н. А
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
Министерство науки и высшего образования Российской Федерации ФГБОУ ВО «Рязанский государственный радиотехнический университет имени В.Ф. Уткина» Кафедра РТС Лабораторная работа №3 «Генерирование коррелированных случайных процессов» Бригада №5 Выполнили: ст. гр. 913 Яковлев Н.А. Перёпелкин М.О. Проверила: Кислицына Т.С. Рязань 2022 г Программа работы: 1. Генерирование некоррелированной случайной последовательности с нормальным законом распределения. 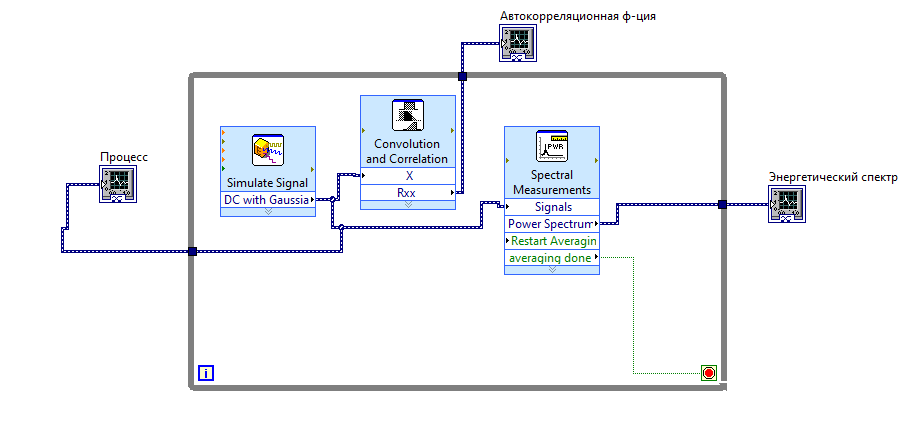 Рис.1 (структурная схема для генерирования некоррелированной случайной последовательности с нормальным законом распределения) 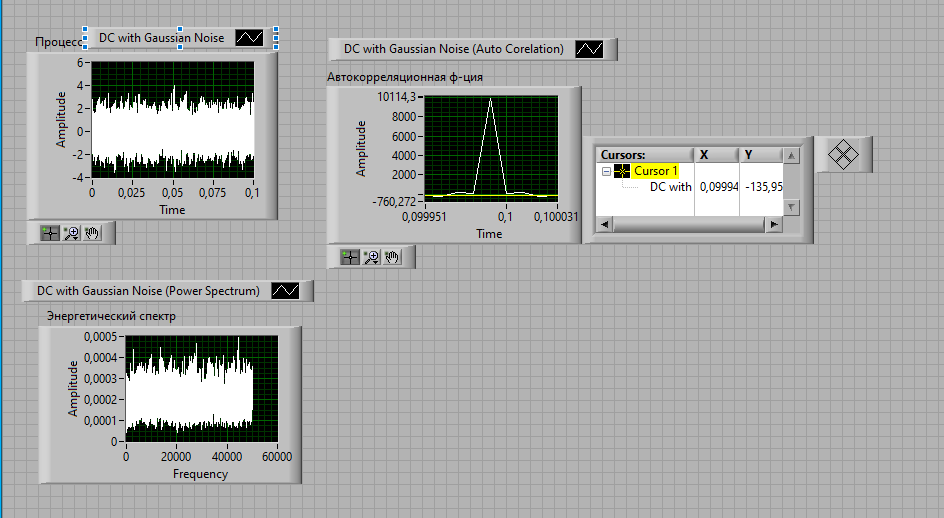 Рис. 2. Случайная последовательность с нормальным законом распределения (процесс, АКФ и энергетический спектр) Вывод: энергетический спектр равномерен во всём диапазоне частот (0…50 кГц). Это говорит о том, что он является белым шумом. Верхняя частота спектра равна 50 кГц, так как она равна fд = 1/Δt. Получается, что при усреднение энергетического спектра происходит уменьшение краевых эффектов (график станет более плавным). 1.1 Рассмотреть пик корреляционной функции и его окрестности в пределах (±5Δt). Измерить интервал дискретизации Δt. Результаты измерений свести в таблицу и сделать вывод о некоррелированности случайного процесса.
Таблица 1. Значения АКФ при изменении времени Интервал дискретизации составляет: Δt = 0,00001 с Вывод: случайный процесс можно считать некоррелированным, так как его корреляционная функция равна нулю для любого τ, отличного от нуля. 2. Генерирование коррелированной случайной последовательности методом формирующего сигнала. 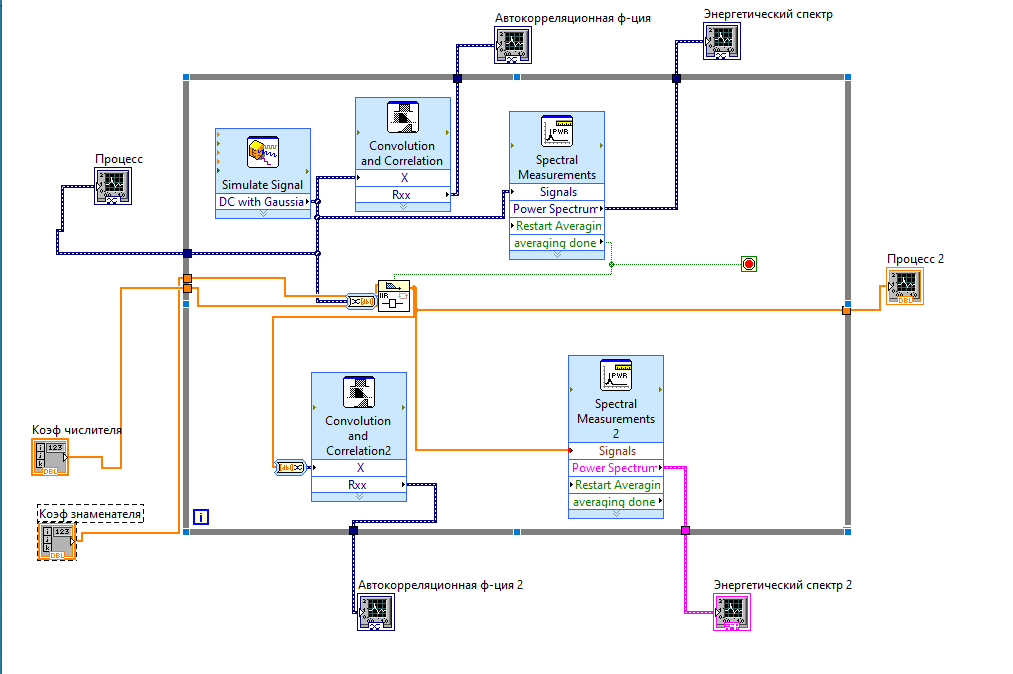 Рис.3 (структурная схема для генерирования коррелированной случайной последовательности методом формирующего сигнала) 3. Исследование СС-фильтра. 3.1. Найти коэффициенты bi CC-фильтра для треугольной корреляционной функции по формуле (3.4) - 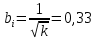 , взяв значения k в соответствии с номером бригады из таблицы. , взяв значения k в соответствии с номером бригады из таблицы.Бригада 5 – k = 9 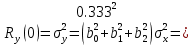 + +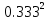 + +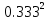 )*9792.9 = 3257.7 )*9792.9 = 3257.7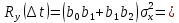 (0.333*0.333+0.333*0.333)* 9792.9 =2171.8 (0.333*0.333+0.333*0.333)* 9792.9 =2171.8 Берем координату в максимуме (АКФ-1): Ϭу = 9792.9 3.2. Замерить автокорреляционную функцию, сравнить ее с теоретической. Посмотреть и зарисовать энергетический спектр в линейном масштабе. Пояснить полученные результаты.   Рис.4 случайная последовательность методом формирующего сигнала (процесс, АКФ и энергетический спектр)
Таблица 2. Значения АКФ при изменении времени Вывод: рассчитанный АКФ совпадает с экспериментально полученным. Так как мы задали одинаковые коэффициенты bi, то корреляционная функция имеет форму треугольника, что сходится с теорией. Так же в результате прохождения сигнала через БИХ-фильтр наблюдается уменьшение пиковых значений и увеличение частоты повторений. 3.3 Сравнить осциллограммы входного и выходного процессов БИХ – фильтра, растянув изображение на графическом индикаторе “Процесс 2” так, чтобы на экране помещалось 50 – 100 отсчетов. Обосновать различие между ними.   Рис.5 Сравнение осциллограммы входных и выходных процессов БИХ-фильтра. Вывод: растянув изображение на графическом индикаторе “Процесс 2” и сравнив с входным процессом можно сказать, что входной процесс имеет более скачкообразную форму, в сравнение с выходным процессом. Объясняется это прохождением сигнала через фильтр, вследствие чего были подавлены ВЧ составляющие исходного сигнала. 3.4 У половины коэффициентов b1 (по вашему усмотрению) изменить знак коэффициентов на обратный (с + на -). Замерить АКФ. Рассчитать АКФ при таких значениях коэффициентов по формуле (3.3). Сравнить рассчитанную АКФ с измеренной. Посмотреть энергетический спектр. Пояснить полученные результаты. 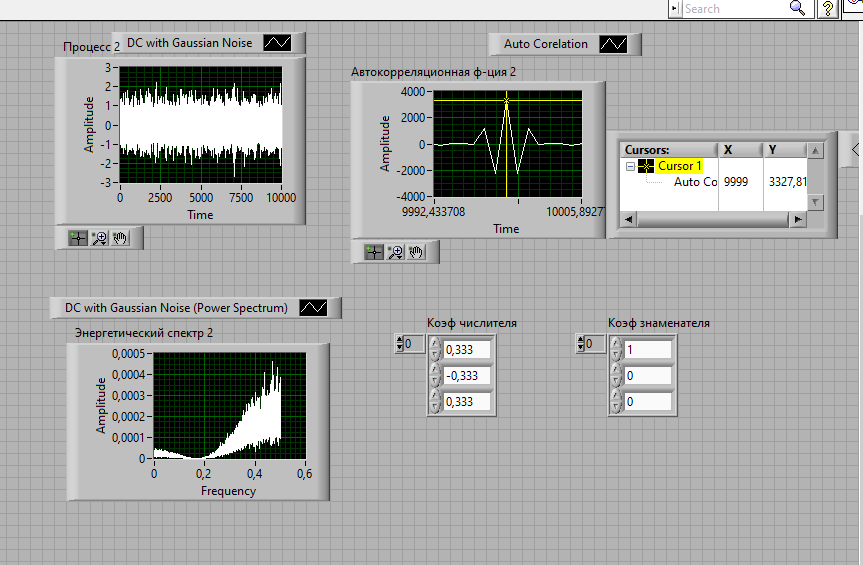 Рис.6 (Моделирование АКФ с разными знаками)
Таблица 3. Значения АКФ при изменении времени Расчет АКФ при измененном знаке в значениях коэффициента по формуле (3.3): b0 = 0.333 b1 = -0.333 b2 = 0.333 Берем координату в максимуме (АКФ-1): Ϭу = 9792.9 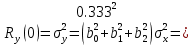 +(- +(- + +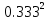 )* 9792.9= 3257.7 )* 9792.9= 3257.7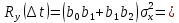 (0.333*(-0.333)+(-0.333)*0.333)* 9792.9=-2171.84 (0.333*(-0.333)+(-0.333)*0.333)* 9792.9=-2171.84
Таблица 4. Сравнение АКФ Вывод: При моделировании используется реализация случайного процесса конечной длины, вследствие чего в АКФ появляются нескомпенсированные остатки, которые и будут являться причиной отклонения экспериментальных данных от расчетных, следовательно, можно сделать вывод, что рассчитанный АКФ совпадает с экспериментально полученным. Также можно сказать, что энергетический спектр имеет подъем в области высоких частот, так как мы изменили знаки коэффициентов фильтра bi. 4. Исследование АР-фильтра второго порядка. 4.1. Сформировать массивы коэффициентов БИХ-фильтра для АР-фильтра с системной функцией: 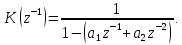 Значение коэффициента α1 = 0.6 взяли из таблицы в соответствии с номером бригады. Коэффициент α2 взять чуть больше -1, мы взяли 0.99. 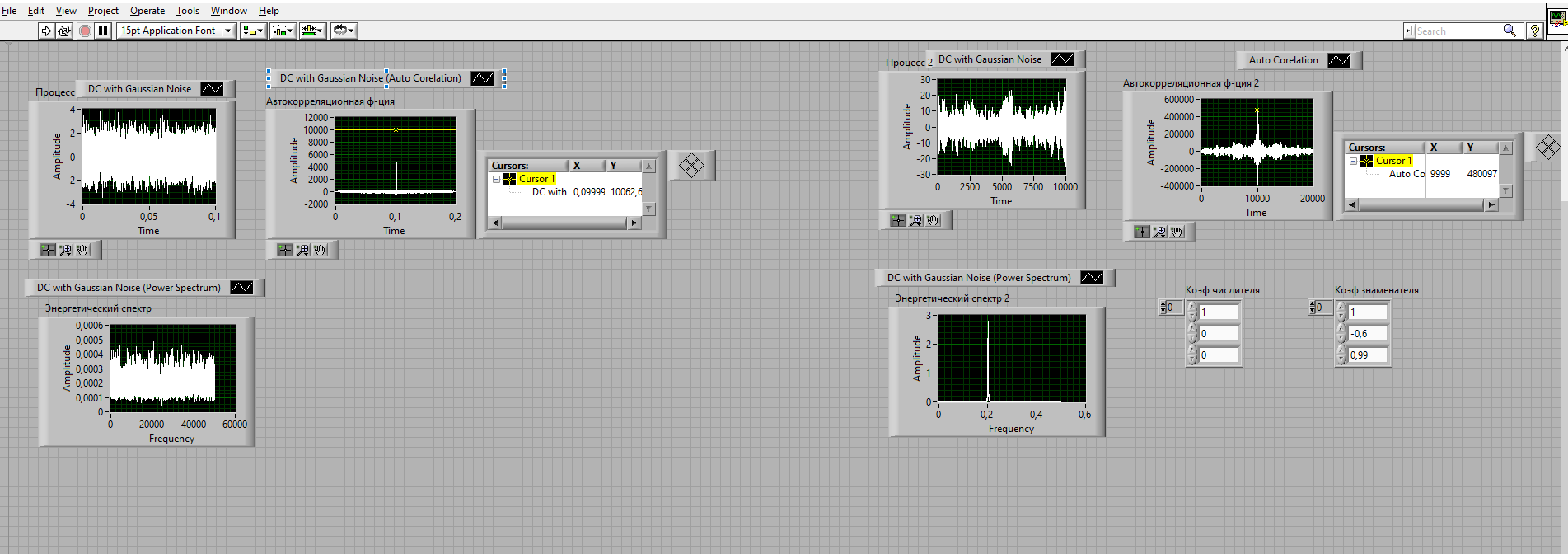 Рис.7 Сформированный БИХ-фильтр 4.2 Проследить изменение корреляционной функции и энергетического спектра с изменением коэффициента α2 от нижней до верхней границы устойчивости в областях A, C и D. Коэффициенты: a1 = 0.6 a2 = -0.1  Рис.8 Процесс, АКФ, энергетический спектр в области А
Таблица 5. Значения АКФ при изменении времени. Вывод: 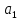 положительный, положительный, 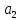 отрицательный, 2 комплексно-сопряженных полюса. Корреляционная функция носит колебательный характер. отрицательный, 2 комплексно-сопряженных полюса. Корреляционная функция носит колебательный характер.Коэффициенты: a1 = -0.6 a2 = 0.1 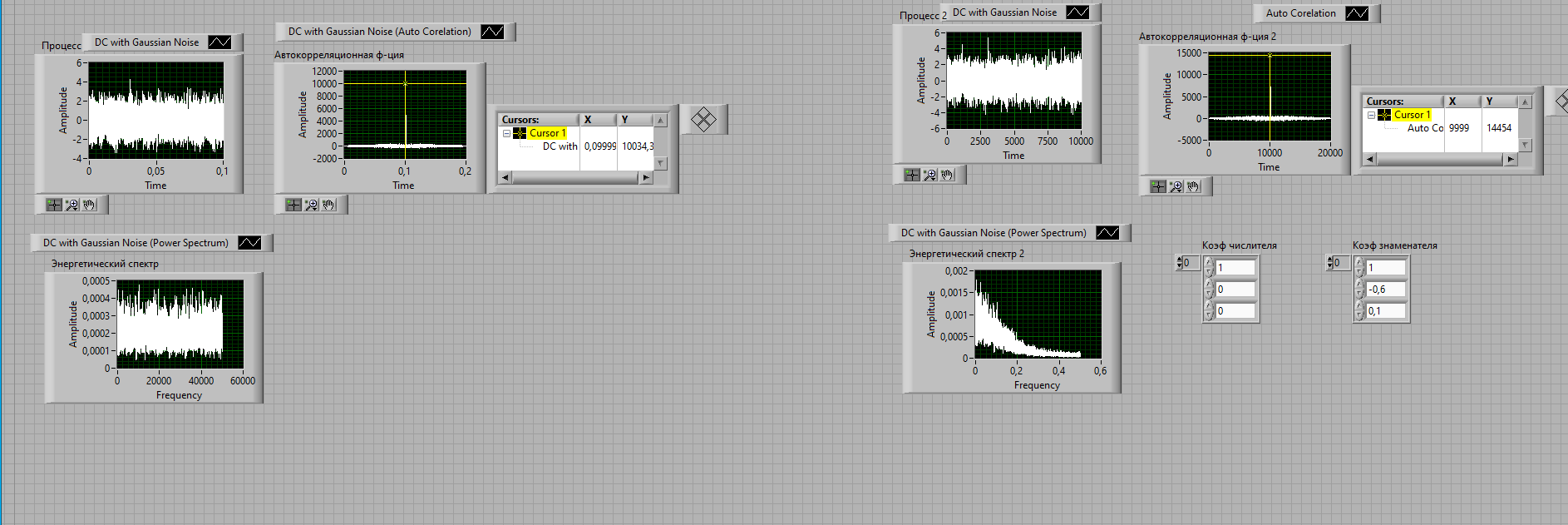 Рис.9 Процесс, АКФ, энергетический спектр в области С
Таблица 6. Значения АКФ при изменении времени. Вывод: 2 действительных полюса. Корреляционная функция будет монотонно спадающей. АЧХ и энергетический спектр имеют подъем в области нижних частот. Коэффициенты: a1 = -0.6 a2 = 0.9  Рис.10 Процесс, АКФ, энергетический спектр в области D
Таблица 7. Значения АКФ при изменении времени. Вывод: 2 комплексно-сопряженных полюса. Корреляционная функция носит колебательный характер. АЧХ имеет подъем в области нижних частот. 4.3. Установить значение коэффициента 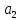 вблизи верхней границы устойчивости (внутри области устойчивости). Проследить изменение корреляционной функции и энергетический спектра с изменением коэффициента вблизи верхней границы устойчивости (внутри области устойчивости). Проследить изменение корреляционной функции и энергетический спектра с изменением коэффициента 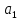 между границами устойчивости. Замерить корреляционную функцию и зарисовать энергетический спектр для трех значений между границами устойчивости. Замерить корреляционную функцию и зарисовать энергетический спектр для трех значений 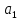 , находящихся вблизи границ устойчивости и посередине области А. , находящихся вблизи границ устойчивости и посередине области А.Левая граница устойчивости: 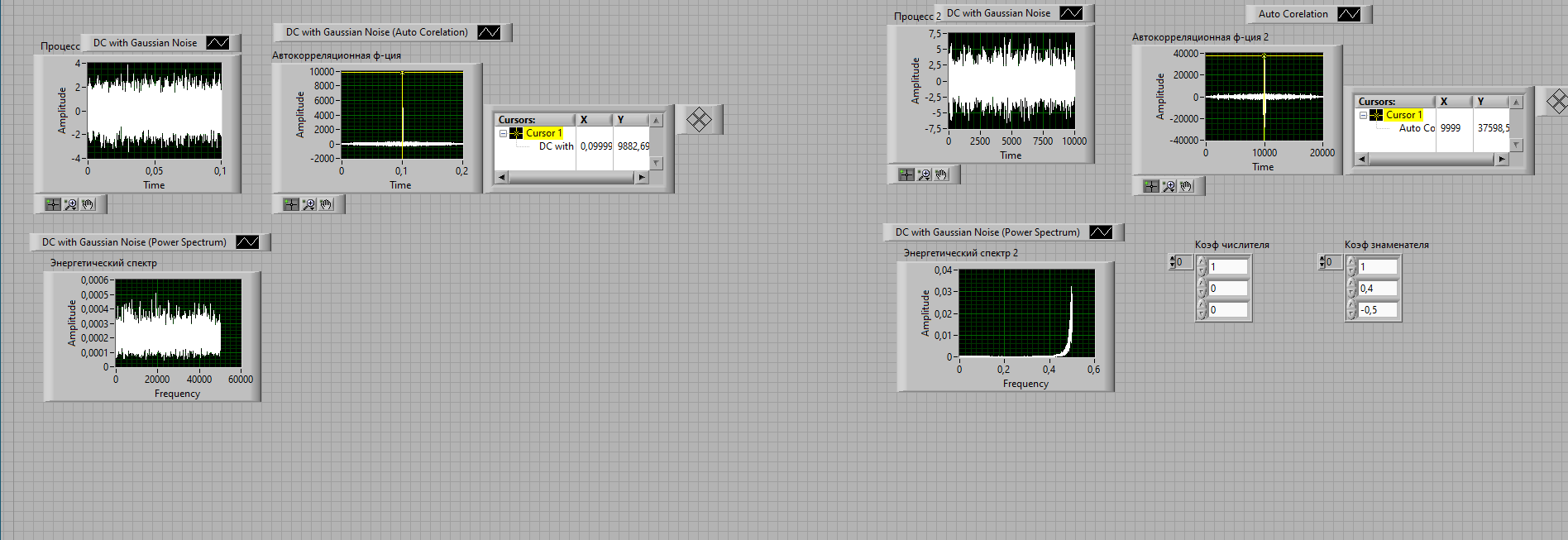 Рис.11. Процесс, АКФ, энергетический спектр выходного сигнала.
Таблица 8. Значения АКФ при изменении времени. Вывод: 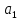 положительный, положительный, 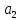 отрицательный, 2 действительных полюса разного знака. Корреляционная функция будет колебательной. АЧХ и энергетический спектр имеют подъем в области верхних частот. отрицательный, 2 действительных полюса разного знака. Корреляционная функция будет колебательной. АЧХ и энергетический спектр имеют подъем в области верхних частот.Правая граница устойчивости: 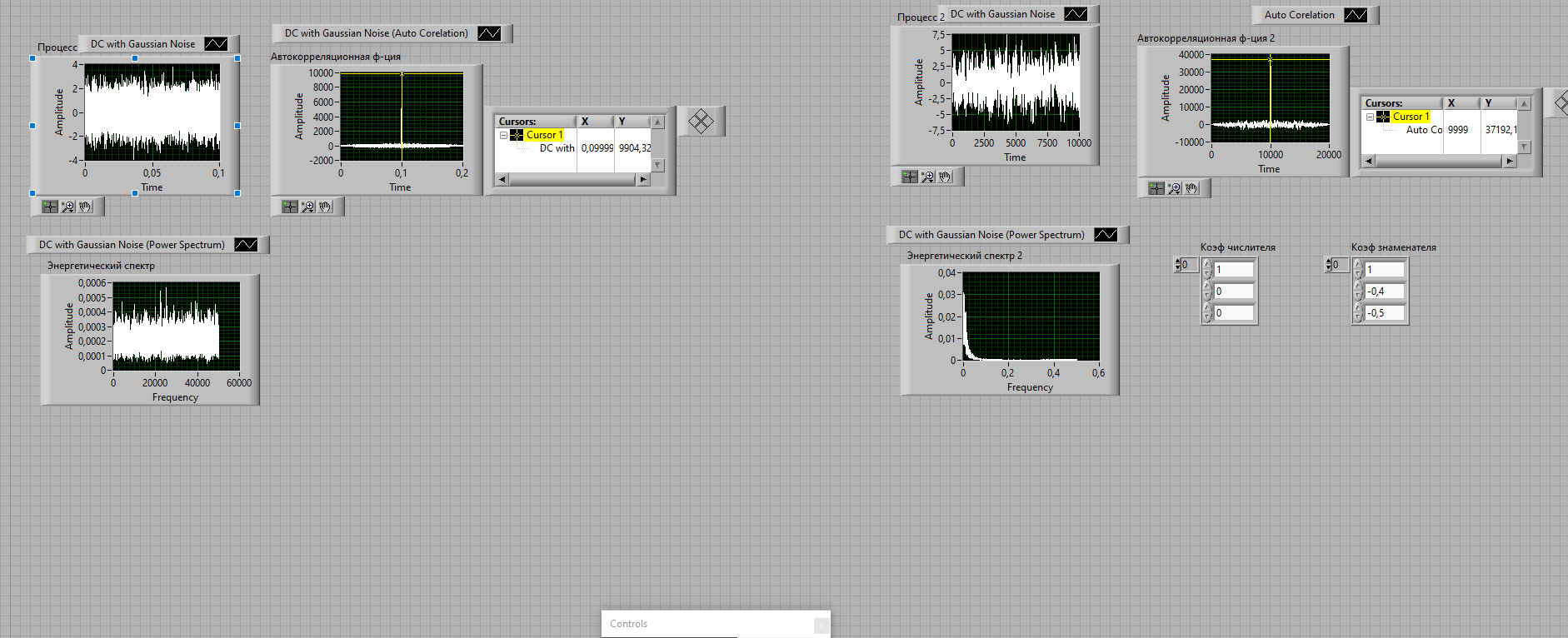 Рис.12. Процесс, АКФ, энергетический спектр выходного сигнала.
Таблица 9. Значения АКФ при изменении времени. Вывод: 2 действительных полюса. Корреляционная функция будет монотонно спадающей. АЧХ и энергетический спектр имеют подъем в области нижних частот. Посередине области А:  Рис.13. Процесс, АКФ, энергетический спектр выходного сигнала.
Таблица 10. Значения АКФ при изменении времени. Вывод: Полюса в этой области действительные, но разного знака. Корреляционная функция будет колебательной. Энергетический спектр имеет подъем в области высоких частот. В данном пункте лабораторной наглядно показано зависимость корреляционной функции от коэффициента аi. Общий вывод: в ходе выполнения лабораторной работы, мы изучили генерирование коррелированных случайных процессов. |