3 лр. Лабораторная работа 3 Определение коэффициента теплоотдачи при естественной конвекции
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Министерство высшего образования и науки Российской Федерации Федеральное агентство по образованию Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет» Кафедра промышленной теплоэнергетики Лабораторная работа №3 Определение коэффициента теплоотдачи при естественной конвекции Вариант 77 Выполнил ст. гр. МПдсЗ-19-01 И.С. Хабибуллин Проверил Е.А. Федосеева Уфа, 2020 Цели работы Углубление знаний по теории конвективной теплоотдачи. Изучение методики исследования процесса теплоотдачи в условиях свободного движения среды Освоение одного из методов определения коэффициента теплопроводности теплоизоляционных материалов (метод трубы) и закрепление знаний по теории теплопроводности Получить навыки в обработке опытных данных в критериях подобия. Задание Определить по предоставленным экспериментальным данным значение коэффициента теплоотдачи при естественной конвекции для горизонтальной трубы и вывести уравнение подобия. Теоретические основы 3.1 Основные понятия Конвекция – процесс переноса теплоты, происходящий за счет перемещения больших масс (макромасс) вещества в пространстве, поэтому наблюдается только в жидких и газообразных телах. Объемы жидкости или газа, перемещаясь из области с большей температурой в область с меньшей температурой, переносят с собой теплоту. Конвекция всегда сопровождается теплопроводностью, т.к. имеет место непосредственное соприкосновение между частицами жидкости, этот совместный процесс называют конвективным теплообменом. Конвективный теплообмен между поверхностью твердого тела и жидкостью или газом называется теплоотдачей. Теплоотдача является достаточно сложным процессом и коэффициент теплоотдачи, а зависит от многих факторов, основными из которых являются: а) причина возникновения течения жидкости; б) режим течения жидкости (ламинарный или турбулентный); в) физические свойства жидкости; г) форма и размеры теплоотдающей поверхности. Главной задачей теории конвективной теплоотдачи является определение количества теплоты, которое проходит через поверхность твердого тела, омываемого потоком. Результирующий поток теплоты всегда направлен в сторону уменьшения температуры. Для расчета стационарного теплового потока при теплоотдаче используют формулу Ньютона-Рихмана, согласно которой тепловой поток пропорционален поверхности теплообмена F и разности температур стенки и жидкости: 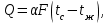 (3.1) (3.1)где Q - тепловой поток, Вт; α - коэффициент теплоотдачи, Вт/(м2·град); F - поверхность теплообмена, м2; tс - температура поверхности теплообмена, °С; tж - температура жидкости, °С. Коэффициент теплоотдачи можно определить как количество теплоты, отданное (принятое) в единицу времени единицей поверхности при разности температур между поверхностью и жидкостью в один градус. 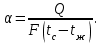 (3.2) (3.2)В общем случае коэффициент теплоотдачи может изменяться вдоль поверхности теплообмена, поэтому различают средний по поверхности коэффициент теплоотдачи и локальный коэффициент теплоотдачи. Коэффициент теплоотдачи имеет следующий порядок для различных условий конвективного теплообмена, Вт/(м2 ·град):
Современные методы расчета конвективного теплообмена основываются на теории пограничного слоя. Несмотря на свою незначительную по сравнению с характерными размерами тела толщину, пограничный слой играет основную роль в процессах динамического и теплового взаимодействия потока жидкости с поверхностью теплообмена. В непосредственной близости от стенки существует вязкий подслой, где теплота передается только теплопроводностью, коэффициент теплоотдачи при этом может быть вычислен по формуле [2]: 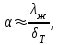 (3.3) (3.3)где λж - коэффициент теплопроводности жидкости, омывающей поверхность теплообмена, Вт/(м·град); δТ - толщина теплового пограничного слоя, м. Теплоотдача является достаточно сложным процессом и коэффициент теплоотдачи, а зависит от многих факторов, основными из которых являются: а) причина возникновения течения жидкости; б) режим течения жидкости (ламинарный или турбулентный); в) физические свойства жидкости; г) форма и размеры теплоотдающей поверхности. Чтобы интенсифицировать теплоотдачу, необходимо использовать жидкости с высокой теплопроводностью и принять меры к уменьшению толщины пограничного слоя. Конвективный перенос может осуществляться в результате свободного или вынужденного движения теплоносителя. Свободное движение или естественная конвекция вызывается действием массовых (объемных) сил: гравитационной, центробежной, за счет протекания в объеме жидкости электрического тока. В приближении сплошной среды под жидкостью мы понимаем любую текучую среду (то, что отлично от твердого тела). Чаще всего в технических устройствах естественная конвекция вызывается подъемной силой, обусловленной разностью плотностей холодных и нагретых частей жидкости. Возникновение и интенсивность свободного движения определяется тепловыми условиями процесса и зависит от рода жидкости, разности температур и объема пространства, в котором происходит конвекция. Вынужденная конвекция вызывается работой внешних агрегатов (насос, вентилятор). Движущая сила при этом непосредственно связана с разностью давлений на входе и выходе из канала, по которому перемещается жидкость. Свободное движение называется также естественной конвекцией. Процесс естественной конвекции возникает из-за различия плотностей холодного и горячего теплоносителей. Для большинства теплоносителей в том интервале температур, который обычно встречается на практике, зависимость плотности от температуры с достаточным приближением может рассматриваться как линейная. Так, если вдали от нагретого тела температура теплоносителя составляет tж, а в некоторой точке около поверхности равна t, то соответствующие значения плотности ρж, ρ связаны уравнением 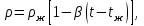 (3.4) (3.4)где β - коэффициент объемного расширения среды. Так как ρ<ρж, то на частицы нагретой жидкости, имеющей температуру t, действует подъемная архимедова сила, равная 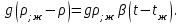 (3.5) (3.5)Эта сила и вызывает конвективное движение среды. Из этого выражения следует, что подъемная сила будет тем больше, чем выше значения напряженности гравитационного поля g, коэффициент объемного расширения β и температурного перепада Δt. Характерная картина свободного движения вдоль нагретой вертикальной (а) и горизонтальной (б) труб показана на рис. 1. 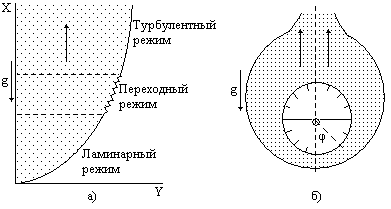 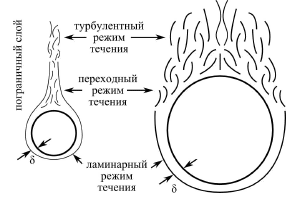 Рис. 1 Вначале толщина движущегося вдоль поверхности нагретого слоя жидкости мала и течение носит ламинарный характер. Постепенно в движение увлекается все большее количество жидкости, толщина ламинарного слоя растет, затем он разрушается и возникает турбулентный режим течения (возникают вихри). В области ламинарного течения коэффициент теплоотдачи уменьшается с увеличением толщины слоя движущейся жидкости, а в области турбулентного течения резко возрастает и далее по высоте стенки сохраняется постоянным. Условия подобия процессов теплообмена при естественной конвекции Конвективный теплообмен описывается системой дифференциальных уравнений и условиями однозначности с большим количеством переменных. Попытки аналитического решения этой системы уравнений наталкиваются на серьезные трудности. В настоящее время точные решения имеются только для отдельных частных случаев. Поэтому большое значение приобретает экспериментальный путь исследования. С помощью эксперимента для определенных значений аргументов можно получить численные значения искомых переменных и затем подобрать уравнения, описывающие результаты опытов. Однако при изучении столь сложного процесса, как конвективный теплообмен, не всегда легко проводить и опытное исследование. Для исследования влияния на процесс какой-либо одной величины остальные нужно сохранять неизменными, что не всегда возможно или затруднительно из-за большого количества переменных. Кроме того, при этом нужно быть уверенным, что результаты, получаемые с помощью какой-либо конкретной установки (модели), можно перенести и на другие аналогичные процессы (образец). Эти трудности помогает разрешить теория подобия. Явления, принадлежащие одному и тому же классу, описываются одинаковыми по физическому содержанию и форме записи дифференциальными уравнениями и называются подобными процессами. Те явления природы, которые описываются одинаковыми по форме записи дифференциальными уравнениями, но различны по своему физическому содержанию, называются аналогичными. Общие условия подобия физических процессов составляют содержание теоремы Кирпичева – Гухмана (1931 г.): 1. Подобные процессы должны быть качественно одинаковыми, т. е. они должны иметь одинаковую физическую природу и описываться одинаковыми по форме записи дифференциальными уравнениями. 2. Условия однозначности подобных процессов должны быть одинаковы во всем, кроме численных значений постоянных, содержащихся в этих условиях. 3. Одноименные определяющие критерии подобных процессов должны иметь одинаковую численную величину. С помощью теории подобия размерные физические величины можно объединить в безразмерные комплексы, причем так, что число комплексов будет меньше числа величин, из которых составлены эти комплексы. Полученные безразмерные комплексы можно рассматривать как новые переменные. При введении в уравнения безразмерных комплексов число величин под знаком функции формально сокращается, что упрощает исследование физических процессов. Кроме того, новые безразмерные переменные отражают влияние не только отдельных одиночных факторов, но и их совокупности, что позволяет легче определить физические связи в исследуемом процессе. Теория подобия устанавливает также условия, при которых результаты лабораторных исследований можно распространить на другие явления, подобные рассматриваемому. Ввиду этого теория подобия является прежде всего теоретической базой эксперимента, но не только. В ряде случаев теория подобия облегчает анализ процесса и описание полученных результатов, хотя с ее помощью вид искомой функции не может быть определен. Прежде всего, подобными могут быть процессы, протекающие в геометрически подобных системах. Необходимой предпосылкой подобия процессов теплообмена при естественной конвекции должно быть подобие температурных полей на поверхностях нагрева или охлаждения. При выполнении этих требований стационарные процессы свободной конвекции будут подобны, если каждое из определяющих чисел подобия (число Грасгофа - Gr и число Прандтля - Рг) в геометрически подобных точках систем будут одними и теми же, т е. Gr = idem; Pr = idem. (3.6) Число Грасгофа характеризует интенсивность свободного движения жидкости и представляет собой отношение подъемной силы, возникающей вследствие теплового расширения жидкости, к силам вязкостного трения. Оно имеет вид 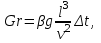 (3.7) (3.7)где g - ускорение свободного падения, м/с2; β - температурный коэффициент объемного расширения, 1/град; Δt- характерная разность температур, град; l- характерный линейный размер системы, м; v - коэффициент кинематической вязкости, м2/с. Число Прандтля является теплофизической характеристикой теплоносителя: 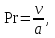 (3.8) (3.8)где а - коэффициент температуропроводности, м2/с. Он характеризует совокупное соотношение между силами инерции и вязкости и потоками теплоты конвективным и кондуктивным. Эти два условия обеспечивают подобие процессов свободной конвекции, т.е. подобие полей температурных напоров, тепловых потоков и скоростей в геометрически подобных системах. При выполнении этих условий определяемое число - число Нуссельта Nu - также оказывается одним и тем же в таких системах: 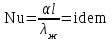 (3.9) (3.9)Число Нуссельта характеризует отношение между потоком теплоты от поверхности тела к жидкости (теплоотдачей) и потоком теплоты теплопроводностью в жидкости у стенки. Критерий Нуссельта - определяемый критерий, так как содержит искомый коэффициент теплоотдачи α. Уравнение подобия (критериальное уравнение) для процессов теплообмена при свободной конвекции в общем виде записывается следующим образом: Nu = f (Gr, Pr ). (3.10) Обобщение опытных данных на основе теории подобия При постановке любого эксперимента всегда необходимо знать заранее: 1) какие величины надо измерять в опыте; 2) как обрабатывать результаты опыта; 3) какие явления подобны изучаемому, т. е. на какие явления можно распространить результаты опытов. На эти вопросы отвечает теория подобия: 1) в опытах нужно измерять все те величины, которые содержатся в критериях подобия изучаемого процесса; 2) результаты опытов необходимо обрабатывать в критериях подобия и зависимость между ними представлять в виде критериальных уравнений; 3) результаты опыта можно распространить на подобные явления, т.е. на качественно одинаковые явления, имеющие подобные условия однозначности и численно равные определяющие критерии. Благодаря этим ответам теория подобия по существу является теорией эксперимента. При обработке результатов опыта, где в качестве рабочей среды был использован воздух, для которого критерий Рг имеет постоянное значение, критериальное уравнение естественной конвекции в общем виде имеет вид Nu=f(Grвозд). В теории конвективного теплообмена принято связь между критериями выражать в виде степенной зависимости 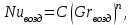 (3.11) (3.11)где Сиn- постоянные величины, определяемые опытным путем. Практически функции такого вида определяются следующим образом: логарифмируя уравнение 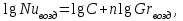 , получим уравнение прямой линии (аналогично уравнению , получим уравнение прямой линии (аналогично уравнению 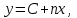 где где 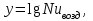 а а 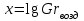 ). ).При этом 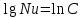 при при 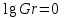 , a , a 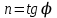 , где φ - угол наклона прямой к оси абсцисс (рис. 2). , где φ - угол наклона прямой к оси абсцисс (рис. 2).- экспериментальные точки; л - точки, выбранные на усредненной прямой 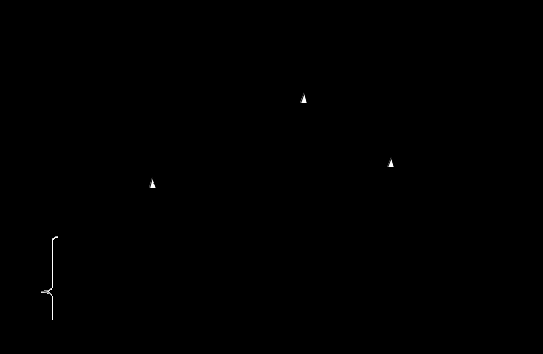 Рисунок 2 По графику значение n определяется как отношение катетов, т. е. 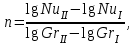 (3.13) (3.13)а значение постоянной С из соотношения 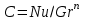 , которую удовлетворяет любая точка прямой. Проверкой применимости степенной зависимости является тот факт, что в логарифмических координатах все опытные точки укладываются на прямую линию. , которую удовлетворяет любая точка прямой. Проверкой применимости степенной зависимости является тот факт, что в логарифмических координатах все опытные точки укладываются на прямую линию.Если же экспериментальные точки в результате ошибки опыта не ложатся на одну прямую, то необходимо провести прямую через равные расстояния от этих точек (усредненную прямую). Затем, взяв на этой прямой две любые точки, определить для них значения 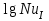 , , 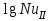 , , 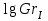 , , 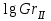 из графика. из графика.В процессе теплообмена при обобщении данных учитывается их изменение с помощью введения слова «определяющий» - определяющей температуры, определяющего размера и т. д. Довольно распространенным является выбор в качестве определяющей температуры 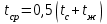 , где tc - температура поверхности (стенки), tж -температура жидкости. Чтобы указать, какая температура принята в каждом конкретном случае в качестве определяющей, в числа подобия вводится соответствующий индекс. Например, если в качестве определяющей температуры принята температура стенки, то ставится индекс «с», если температура потока - индекс «ж», если средняя - индекс «m». , где tc - температура поверхности (стенки), tж -температура жидкости. Чтобы указать, какая температура принята в каждом конкретном случае в качестве определяющей, в числа подобия вводится соответствующий индекс. Например, если в качестве определяющей температуры принята температура стенки, то ставится индекс «с», если температура потока - индекс «ж», если средняя - индекс «m».В условия однозначности может входить несколько размеров. Определяющим считается тот, от которого процесс теплоотдачи зависит в наибольшей степени (обтекание пластины – ее длина, движение жидкости в длинной трубе – ее диаметр и т. д.). В ряде случаев (теплообмен при фазовых переходах) за линейный размер принимается комбинация разнородных физических величин, входящих в условия однозначности, которая имеет размерность линейной величины и пропорциональна какому-либо линейному размеру. При использовании критериальных уравнений всегда нужно обращать внимание на то, какой размер автор формулы ввел в критерии подобия в качестве определяющего. Неучет этого обстоятельстваможет привести к значительным ошибкам. В качестве определяющего размера принимается обычно гот размер, вдоль которого развивается процесс. Если это длина, то ставится индекс «1», а если диаметр - индекс «d», если высота - индекс «h». Поэтому числа подобия могут быть написаны, например, так: Red,ж, Nul,c, Nuh,ж и т.п. Сложный теплообмен В действительных условиях работы различных теплообменных устройств теплота передается одновременно теплопроводностью, конвекцией и излучением. От наружной поверхности изоляционного слоя данной установки теплота передается одновременно конвекцией и излучением, т.е. 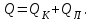 (3.14) (3.14)Лучистый поток от поверхности изоляционного материала в окружающую среду может быть вычислен по формуле 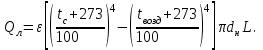 (3.15) (3.15)Тогда конвективная составляющая теплового потока определится из (3.14) как разность 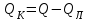 , а коэффициент конвективной теплоотдачи из уравнения Ньютона - Рихмана: , а коэффициент конвективной теплоотдачи из уравнения Ньютона - Рихмана: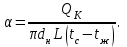 (3.15) (3.15)Лабораторная установка Лабораторная установка (рис. 3) состоит из горизонтальной стальной трубы 4, покрытой слоем изоляционного материала 7, милливольтметра 8, термопар 1 и 2, трансформатора 6, ваттметра 5 и электронагревателя 3. Горизонтальная труба имеет длину L м. Цилиндрический слой изоляционного материала имеет наружный диаметр dн, м. Электронагреватель в виде спирали смонтирован внутри трубы. Мощность регулируется трансформатором и измеряется ваттметром. Наружная средняя температура замеряется при помощи термопар, горячие спаи которых соответственно расположены внутри и снаружи изоляционного слоя, а холодные вынесены на клеммы милливольтметра. Термопары подключены к милливольтметру посредством переключателя. Таблица размеров dвн, dн, L экспериментального участка вывешена около лабораторной установки. 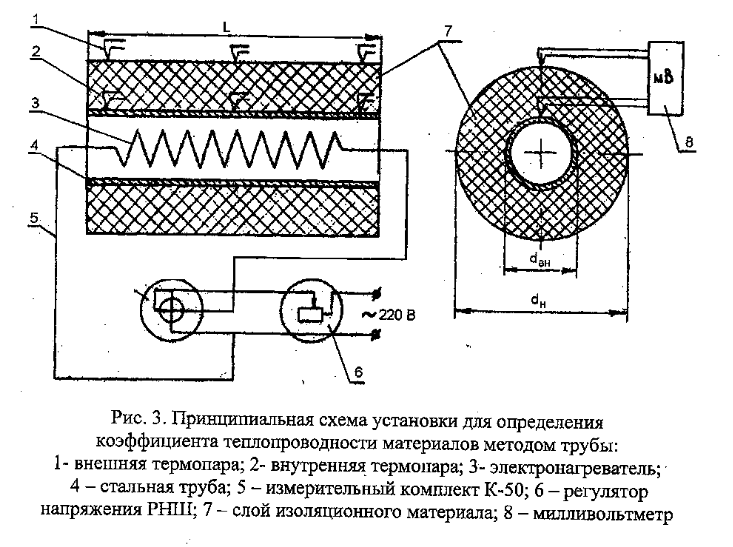 5 Результаты эксперимента: Данные, получаемые в результате эксперимента, представлены в табл.1. Таблица 1. Исходные данные для лабораторной работы
Переведем показания вольтметра по градуировочной таблице в ⁰С: 1) 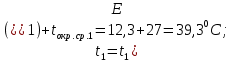 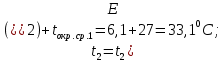 2) 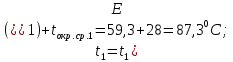 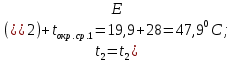 3) 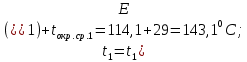 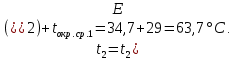 Обработка опытных данных для каждого режима ведется в следующей последовательности. Тепловой поток, Вт: 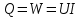 1) 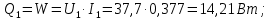 2) 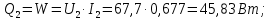 3) 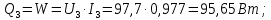 Геометрические размеры установки, м: Внутренний диаметр изоляции dвн = 0,042 м; Внешний диаметр изоляции dн = 0,054 м; Длина экспериментального участка L = 0,6 м. 3. Тепловой поток от наружной поверхности изоляции в окружающую среду излучением: 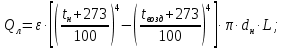 1) 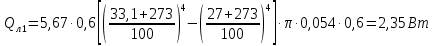 2) 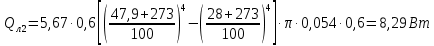 3) 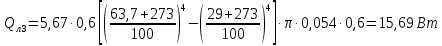 4. Тепловой поток от внешней поверхности изоляции в окружающую среду естественной конвекцией: 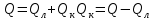 1) 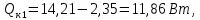 2) 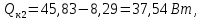 3) 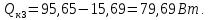 5. Коэффициент конвективной теплоотдачи: 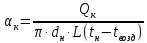 1) 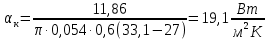 2) 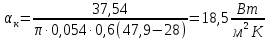 3) 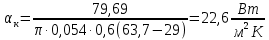 6. Теплофизические свойства воздуха, входящие в числа подобия: 1) 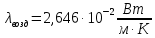 , ,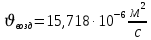 , ,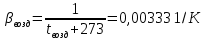 2) 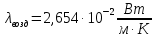 , ,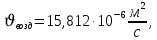 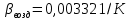 3) 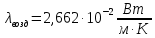 , ,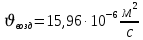 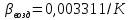 . .7. Критерий Нуссельта: 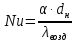 1) 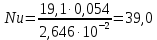 2) 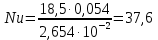 3) 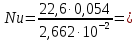 45,8 45,88. Критерий Грасгофа: 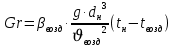 1) 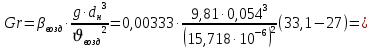 0,13 0,13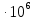 1) 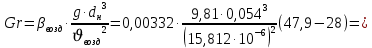 0,41 0,41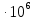 1) 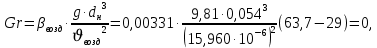 70 70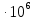 9. Построим зависимость 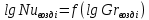 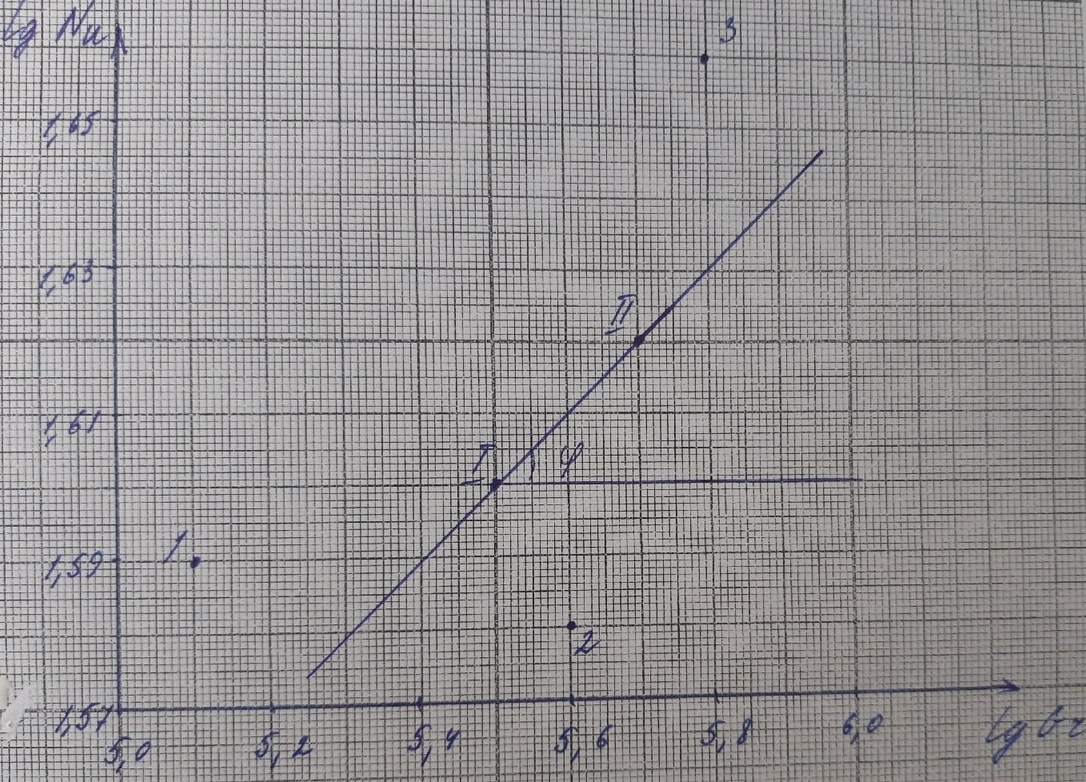 Рисунок 4 - Зависимость 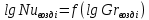 10. Показатель n: 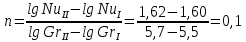 11. Постоянная С: 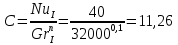 12. Критериальное уравнение в явном виде: 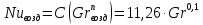 13. Максимальная погрешность измерения среднего коэффициента теплоотдачи: 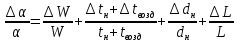 1) 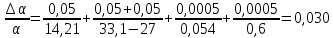 2) 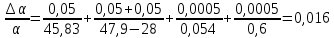 3) 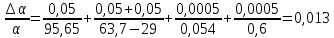 Вывод: В ходе лабораторной работы экспериментально определили коэффициент теплоотдачи на поверхности горизонтальной трубы при естественной конвекции, были определены критерии подобия и построены в логарифмических координатах зависимость 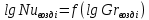 , по которой выведено критериальное уравнение в явном виде: , по которой выведено критериальное уравнение в явном виде: 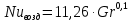 . .Была рассчитана максимальная погрешность измерения среднего коэффициента теплоотдачи для каждого режима: 0,030; 0,016; 0,013. |
