Лабораторная работа №3. Лабораторная работа 3 Табулирование функций и построение графиков
 Скачать 1.11 Mb.
|
Лабораторная работа 3Табулирование функций и построение графиковЦель работы: изучить операцию заполнения ячеек данными; изучить операцию копирования формул с помощью заполнения; научиться решать расчетные задачи табулирования функции одной переменной для шагового аргумента; рассмотреть вопросы вычисления таблиц функций, заданных различными аналитическими выражениями, функций, зависящих от параметра, функций заданных в параметрической форме или в полярной системе координат. 1. Приемы копирования и заполнения ячеек1.1 Абсолютные, относительные, смешанные ссылкиНапомним, что ссылка вида A1 называется относительной. Относительная ссылка меняется при копировании формулы из одной ячейки в другую, так что сохраняется относительное расположение влияющих на формулу ячеек и ячейки, содержащей формулу. Это позволяет создать расчетные таблицы, содержащие повторяющиеся вычисления для данных, находящихся в различных ячейках. Пример. В ячейку C3 введена формула =(A2+A3+A4)/3. При ее копировании в ячейку С4 получим формулу =(A3+A4+A5)/3. При копировании в ячейку F10 получим формулу =(D9+D10+D11)/3. Просмотреть зависимые и влияющие ячейки можно с помощью панели Зависимости. Она вызывается по команде Вид|Панели инструментов|Настройка, вкладка Панели инструментов, установить флажок Зависимости. Затем выделяется ячейка с формулой. При нажатии кнопки Влияющие ячейки появляются стрелки от влияющих ячеек к зависимым. Кнопка Зависимые ячейки показывает, на какие ячейки с формулами влияет данная ячейка. Для снятия стрелок используется кнопка Убрать все стрелки. Ссылка вида $A$1 называется абсолютной. При копировании формул абсолютные ссылки не меняются. Это позволяет использовать константы в повторяющихся вычислениях. Ссылка вида $A1 называется смешанной. При копировании формулы со ссылкой данного типа не меняется заголовок столбца, а номер строки может меняться. Наоборот, при использовании другой смешанной ссылки типа A$1 не меняется номер строки, а заголовок столбца может меняться. 1.2. Заполнение ячеекЗаполнение ячеек - это перенос данных из одной ячейки в ряд смежных ячеек строки или столбца с возможностью их изменения по некоторому закону. Операция выполняется по команде Правка|Заполнить…. В диалоговом окне команды можно указать различные варианты заполнения. Вычисление значений аргумента по типу арифметической или геометрической прогрессии. Порядок работы следующий: ввести первое значение в требуемую ячейку и выделить эту ячейку, вызвать команду Правка|Заполнить|Прогрессия. В ее диалоговом окне установить расположение данных (строки, столбцы), тип прогрессии, шаг изменения аргумента, предельное значение аргумента. После подтверждения команды (OK) столбец (или строка) будет заполнен. в направлении увеличения адресов. Заполнение ячеек заголовками строк или столбцов вида Урок 1, Урок 2, и т.д. выполняется так: вводится первый заголовок, выделяется заполняемый диапазон ячеек и выполняется команда Правка|Заполнить|Прогрессия. В диалоговом окне команды выбирается Автозаполнение. Возможно заполнение последовательных ячеек датами с заданным интервалом, названиями месяцев, дней недели, годов, часов. Предлагаем эту операцию освоить самостоятельно экспериментальным путем с помощью все той же команды Правка|Заполнить |Прогрессия. Заполнение ячеек формулами разберем на примере построения таблицы значений функции. Предварительно отметим следующее: при копировании формул из одних ячеек в другие, обычные (так называемые относительные) ссылки на ячейки изменяются с сохранением структуры зависимости от исходных данных. Например, введем в ячейку B1 формулу =A1+5. При копировании формулы в нижележащую ячейку B2 она превращается в формулу =A2+5. Заполнение ячеек формулами есть не что иное, как копирование формул в последовательные ячейки таблицы. Оно выполняется следующим образом: формула вводится в первую ячейку ряда, затем нужно выделить диапазон для ввода формул и применить команду Правка|Заполнить| Вниз (или Вправо). Замечание. Если ссылка на ячейку в формуле является абсолютной ($A$10), то при копировании формулы она не меняется. Например, формула =$A$10+A1 при копировании изменит ссылку лишь на ячейку A1. Добавление. Можно быстрее выполнять команду заполнения с помощью Маркера заполнения. Данные типа арифметической прогрессии вводятся в две первые ячейки заполняемого ряда. Затем, выделив эти ячейки, нужно установить указатель мыши на Маркер заполнения - маленький черный квадрат в правом нижнем углу выделенного диапазона и протащить указатель вдоль заполняемого столбца до появления последнего значения. При отпускании мыши ряд будет заполнен данными. Заполнение ячеек формулой выполняется аналогично, но только еще проще - достаточно протащить формулу за маркер заполнения вдоль требуемого ряда. 2. Примеры построения таблиц значений и графиков функцийПример 1. ( Функция одной переменной для шагового аргумента). Построить таблицу значений функции  для аргумента x, изменяющегося от 0 до 1,5 с шагом 0,1. Построить график функции.Решение. Решение разбивается на два основных этапа: построение таблицы значений функции и построение графика функции. Построение таблицы Наберем заголовки столбцов для x и y в ячейках A1, B1. Наберем первое значение x, равное 0, в ячейку A2. Выполним команду Правка|Заполнить|Прогрессия, зададим в диалоге Расположение в столбце, Арифметическая прогрессия, Шаг 0,1, Предельное значение 2. Заполнятся ячейки A4:A22. В ячейку B2 введем формулу: =SIN(4*A2)^2/(A2+1) и скопируем ее в ячейки B3:B22 Выполним форматирование данных (чисел) и обрамление таблицы. Фрагмент рабочего листа с таблицей показан на рис.1. Построение графика функции. Для построения графика выделим диапазон данных (ячейки A1:B22) и построим точечную диаграмму, вид которой представлен на рис.2. Рис.1. Таблица значений функции для примера 1   Рис. 2. График (точечная диаграмма) примера 1 Рис. 2. График (точечная диаграмма) примера 1 Пример 2. (Функция, заданная различными аналитическими выражениями (сложная функция)). Построить таблицу значений и график функции  для аргумента x , изменяющегося от -2 до 2 с шагом 0,2 РешениеПостроение таблицы. Решение выполним в том же файле, что и предыдущий пример, но на новом листе Excel. Последовательность заполнения ячеек аналогична примеру 1. В ячейку B2 введем формулу: =ЕСЛИ(A2<0;-A2/(ABS(A2)+1);SIN(ПИ()*A2)) и скопируем ее в нижележащие ячейки для всех значений x . П Рис..4. График сложной функции Рис. 3. Таблица значений сложной функции   остроение графика функции также полностью аналогично построению предыдущего примера, если заданная функция непрерывна. Замечание. Если функция терпит разрыв при переходе от одного аналитического выражения к другому, то нужно построить на одной диаграмме два графика, каждый из которых отвечает области непрерывности функции. В случае разрывной функции можно строить один график, если выбрать вид графика из отдельных точек Пример 3. (Функция, зависящая от параметра). Построить таблицу значений и график функции  для аргумента x, изменяющегося от -1 до 3 с шагом 0,2 при заданных значениях a и b.РешениеВведем заголовки столбцов для x и y в ячейки A1, B1 и значения a, b в отдельные ячейки D1, F1. Заполним столбец A2:A22 значениями x. Введем формулу для y в ячейку B2 =EXP($D$1*A2)*COS($F$1*A2) и скопируем ее в ячейки B3:B22. П Рис..5. Таблица и график функции, зависящей от параметра 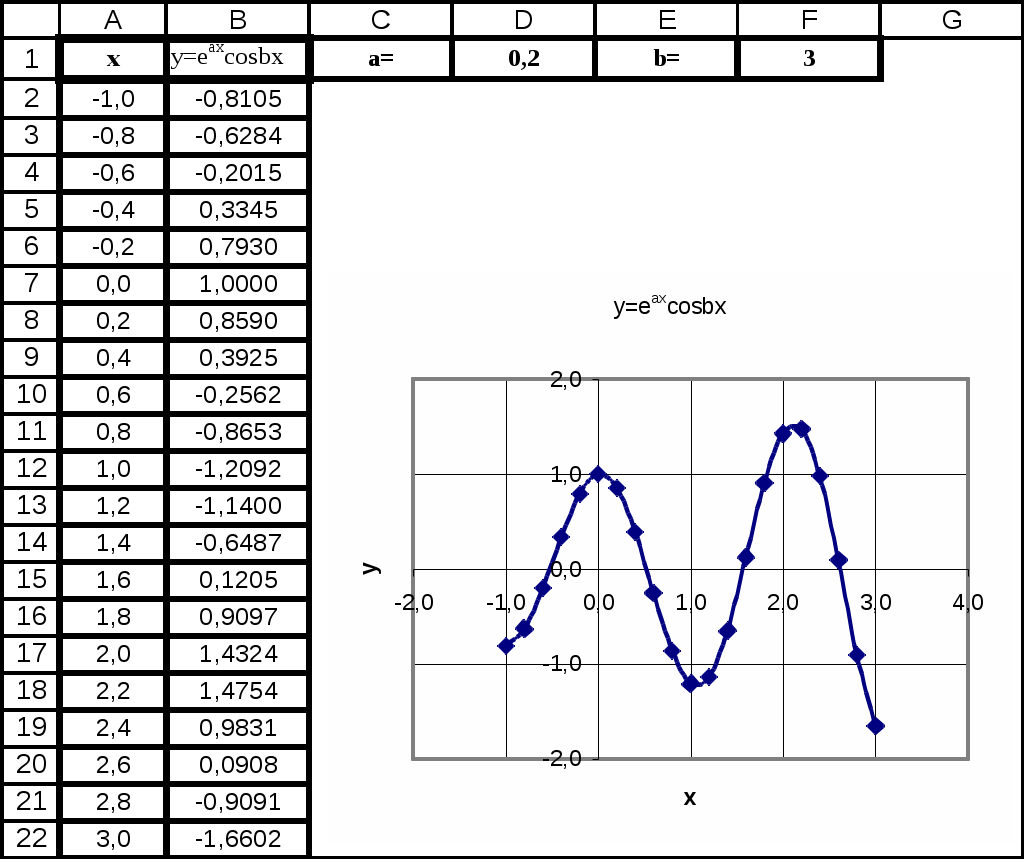 остроим график аналогично примеру 1 (см. рис.5.5) Замечание. Меняя значения параметров, можно получить совершенно другое поведение функции. Рекомендуется проанализировать поведение функции при a>0 и a<0, а также рассмотреть уменьшение и увеличение b. Пример 4. (Функция, заданная параметрическими уравнениями). Вычислить таблицу значений функции, заданной параметрическими уравнениями и построить ее график. В качестве примера рассмотрим построение окружности. Параметрические уравнения окружности рассмотрим для значений параметра, пробегающих полный оборот вокруг начала координат:  (1)Построение таблицы значений функции Перейдем на новый рабочий лист. Зададим заголовки столбцов t, x, y. Заполним первый столбец значениями t, применив еще один способ задания аргумента: каждое последующее значение вычислим через предыдущее, добавляя шаг. В ячейке D2 вычислим  по формуле =ПИ()/16. В ячейку A2 введем 0, в ячейку A3 введем формулу =A2+$D$2, которую копируем вниз до значения 2.Введем в ячейку B2 формулу =COS(A2); в ячейку C2 формулу =SIN(A2) Выделим ячейки B2, C2 и копируем их для всех значений t с помощью заполнения. Форматируем таблицу по образцу. Построение графика функции Выделим диапазон B2:C23 Вызовем Мастер диаграмм и построим точечную диаграмму. В процессе построения зададим заголовки диаграммы и осей, уберем легенду, назначим линии сетки. Затем отредактируем диаграмму: по команде Формат оси зададим точность – один знак после запятой, по команде Формат области построения укажем рамку Невидимая. Выполним растяжение-сжатие диаграммы, так чтобы получилась окружность, а не эллипс. Результат построения показан на рис.7. Рис. 7. График функции, заданной параметрическими уравнениями  Рис.6. Таблица функции, заданной параметрическими уравнениями  Замечания1. Несколько изменив уравнения (1) можем получить и параметрические уравнения эллипса. Как работать с функциями, содержащими постоянные параметры, было рассмотрено в предыдущем примере. Итак, эллипс с осями a, bзадается уравнениями:  где a, b - положительные константы2. В примерах 1-3 были рассмотрены функции, заданные аналитически в явном виде, т.е. формулой, в которой зависимая переменная yвычислялась через независимую переменнуюx. Существует другой способ задания функции, в котором обе этих величины являются функциями одного и того же параметра t. Тогда каждому значению t соответствует пара значений (x, y), определяемых формулой  (2)Предположим, что по каждому значению x=f(t) можно найти единственное значение t, которому в свою очередь можно сопоставить y=g(t). Тогда можно считать y функцией x. Такой способ задания функции называется параметрическим. Если рассматривать множество пар (x,y), определяемых уравнением (2) как множество точек на плоскости, то уже нет необходимости требовать единственности решения tпо x. И в этом случае считаем, что задана функция yот x параметрическими уравнениями (2). Может оказаться, что одному значению xсоответствует два или даже несколько значений y. В ряде случаев простые параметрические уравнения позволяют задать функции, для которых явные уравнения очень сложны или не существуют. 3. Функция, заданная в полярной системе координат, легко преобразуется к параметрической форме. Действительно, декартовы координаты x, yсвязаны с полярными координатами , уравнениями  (3)Если задано уравнение кривой в полярной системе координат  , то подставив это выражение в уравнения (3), получим параметрические уравнения кривой с полярным углом в качестве параметра.3. Варианты заданийЗадача 1. Вычислить таблицу значений функции для аргумента, изменяющегося с данным шагом в заданном интервале, и построить ее график
Задача №2. Построить график функции. Значения аргумента задать таким образом, чтобы получить на графике не менее 15 точек. Для автоматизации вычислений использовать функцию ЕСЛИ. Таблица 2 .
Задача 3. Вычислить таблицу значений функции, заданной параметрическими уравнениями или уравнением в полярной системе координат, и построить ее график. В случае задания функции в полярной системе координат перейти к параметрическим уравнениям. Константы, входящие в уравнения, являются положительными и, если не задано их конкретное значение, могут быть взяты равными единице. Таблица 3
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
