Исследование механизмов прерывистого движения. Лабораторная работа 4 Исследование механизмов прерывистого движения Проверил Выполнили Баранов В. В. ст гр. 913301 Илясов В. Р
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
Министерство образования Республики Беларусь Учреждение образования «БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ» КАФЕДРА КОМПЬЮТЕРНОГО ПРОЕКТИРОВАНИЯ Лабораторная работа № 4 «Исследование механизмов прерывистого движения» Проверил: Выполнили: Баранов В.В. ст. гр. 913301 Илясов В. Р. Асиненко А. М. Денскевич А. Д. Минск, 2021 Цели работы Ознакомиться с конструкциями мальтийских, храповых механизмов прерывистого движения. Получить навыки в составлении кинематических схем. Исследовать кинематические параметры мальтийского механизма. Основные положения Работа ряда переключающих устройств в системах настройки и управления, устройств транспортирования, полуавтоматических и автоматических технических систем требует наличия периодических остановок определенной длительности, прерывистости движения ведомого звена. Для получения такого движения кроме кулачковых механизмов применяют мальтийские и храповые механизмы, а также механизмы с неполными зубчатыми колесами. Мальтийские механизмы служат для преобразования равномерного вращательного движения ведущего звена (кривошипа) в периодические повороты с остановками ведомого звена, креста. Эти механизмы в сочетании с зубчатыми передачами используют для прерывистого движения лент, в многопозиционных устройствах – автоматах и т.д. Различают два типа мальтийских механизмов: с внешним (рис. 17.1, а) и внутренним (рис. 17.1, б) зацеплениями. Чаще применяют механизмы внешнего зацепления. При вращении кривошипа 1 (рис. 17.1, а) его палец (цевка) В входит в паз креста 2 и, поворачиваясь на угол φ′1р, поворачивает крест на рабочий угол φ2р, после чего выходит из прорези. Вращение ведомого креста прекращается. Он остается неподвижным, пока кривошип не повернется на угол 2π –φ1р до входа ведущей цевки в следующий паз креста. 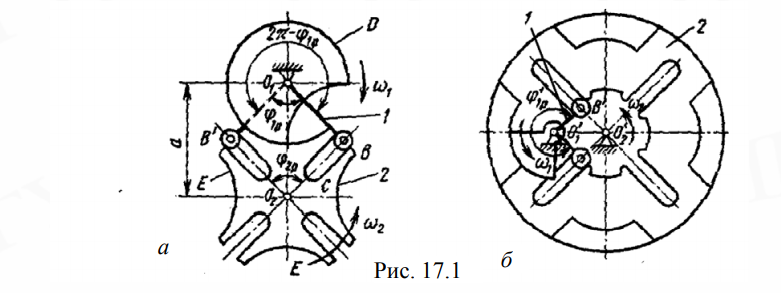 Стопорение креста в неподвижном положении происходит с помощью секторного замка. Выпуклая цилиндрическая поверхность D диска входит в соприкосновение с вогнутой поверхностью Е креста и препятствует его повороту. Диск закреплен на кривошипе 1 в определенном положении и имеет вырез для прохода крестовин ведомого звена. В механизме с внутренним зацеплением (рис. 17.1, б) кривошип 1 и крест 2 вращаются в одном направлении, отношение угла поворота кривошипа φ′1р к углу поворота креста φ2р значительно больше, чем в механизме внешнего зацепления. Этот механизм может иметь только одну цевку. Механизмы с внутренним зацеплением являются конструктивно более сложными, но имеют меньшие габаритные размеры и меньшие угловые ускорения креста, т.е. меньшие динамические нагрузки. Мальтийские механизмы внешнего зацепления могут иметь несколько цевок на кривошипе, что позволяет получить равные (рис. 17.2, а) и не равные (рис. 17.2, б) интервалы перемещений и остановов за один оборот ведущего звена. Для обеспечения плавного, безударного вращения креста в начале и конце поворота направление линейной скорости пальца кривошипа в момент входа и выхода из паза должно совпадать с осью прорези. Это условие будет соблюдаться, если углы О1ВО2 и О1В′О2 будут равны π/2. Угол поворота креста φ2р = 2π/z2, где z2 – число пазов креста. Рассматривая четырехугольник О1ВО2В′ (рис. 17.1, 17.2), получим  (здесь и далее верхний знак (–) – для внешнего зацепления, нижний (+) – для внутреннего).  Для мальтийского механизма с одной цевкой цикл соответствует одному обороту кривошипа. Время цикла tц состоит из времени поворота t2р креста и времени его покоя t2п. Отношение t2p/tц называют коэффициентом времени движения. При kд = 1 крест вращается непрерывно, без остановок. Из (17.2) следует, что при одной цевке (z1 = 1) коэффициент kд зависит только от числа пазов z2 креста. Анализируя зависимость (17.2) отметим, что прерывистое движение возможно, т.е. kд > 0 при числе пазов z2 ≥ 3. В механизме с внешним зацеплением при z2 = 2 коэффициент времени движения kд = 0. Наименьшее значение коэффициента kд при z2 = 3 равно 1/6. При числе цевок z1 > 1 (внешнее зацепление) время цикла tц′ = 2π/(ω1z1) и коэффициент времени движения Из выражения (17.3) число цевок z1 и число пазов z2 креста должно находиться в следующей зависимости: Например, при z2 = 4 число цевок должно быть меньше четырех, т.е. z1 может быть равно 1, 2 или 3. При малом числе пазов выходное звено мальтийского механизма имеет плохие динамические характеристики. Например, при одинаковой скорости кривошипа максимальное угловое ускорение креста с тремя пазами в 45 раз больше, чем у восьмипазового креста. На практике чаще всего применяют механизмы с числом пазов 4, 6 и 8. Мальтийские механизмы могут иметь несколько цевок на ведущем звене (рис. 17.3, а) или несколько ведомых звеньев (крестов) при одной цевке (рис. 17.3, б) с числом пазов в каждом более четырех. На рис. 17.3, б представлены шестипазовые мальтийские механизмы. Исходными данными для расчета геометрических размеров элементов мальтийского механизма являются межосевое расстояние а, число пазов z2 = 3 … 12. Из условия, что угол О1ВО2 (см. рис. 17.2) равен π/2, выразим через межосевое расстояние а радиус кривошипа и максимальный радиус креста 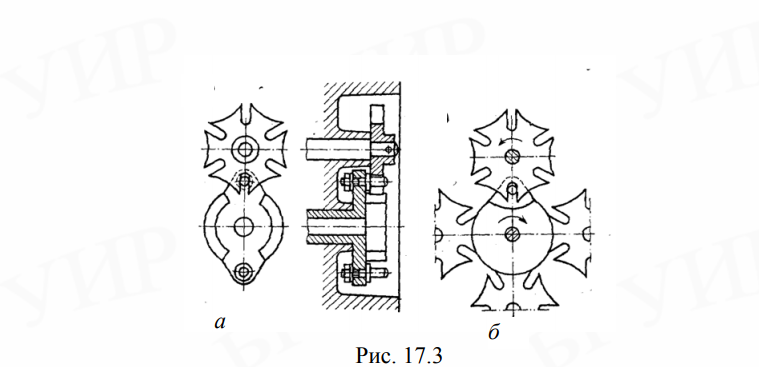 Ведомое звено (см. рис. 17.1, а) мальтийского механизма вращается с переменной скоростью. Скорость креста равна нулю в начале и конце поворота. Максимальную скорость ω2max ведомое звено имеет при прохождении цевки через линию центров О1О2. Из равенства линейных скоростей в точке касания цевкой креста имеем где r2min = а – r1 = a[1 – sin(π/z2)] – расстояние от оси вращения креста, т.е. точки О2 до цевки. Из выражения (17.7) имеем  В этом положении угловое ускорение креста ε2 равно 0, а в начальный и конечный моменты его движения Механизмы с мальтийским крестом работают плавно, без ударов в начале и конце поворота ведомого звена. Ширину dп и длину ℓ пазов креста находим по формулам Для обеспечения низкого коэффициента трения между пальцем кривошипа (цевкой) и рабочими поверхностями креста и высокой износоустойчивости этих элементов в качестве пальца применяют ролик или стандартный подшипник качения. Трение скольжения пальца о рабочие поверхности креста заменяется при этом трением качения. Обычный материал креста – сталь 40Х, пальца – ШХ15. Диаметр оси ролика пальца кривошипа d0 принимают (0,5 … 0,6)dп. Для уменьшения трения в зацеплении рабочие поверхности пазов и цевки обильно смазывают. Храповые механизмы Храповые механизмы позволяют получить прерывистое, с остановами, вращательное или поступательное движение (рис. 17.5). Простейший храповый механизм состоит из ведущего звена 1, совершающего качательное (рис. 17.5, а, б) или возвратно-поступательное (рис. 17.5, в) движение; ведомого звена 2 – храпового колеса (рис. 17.5. а, в) или храповой рейки (рис. 17.5, б) с зубьями специального профиля и неподвижного звена (стойки). Движение от ведущего звена 1 к ведомому 2 передается с помощью собачки 3, шарнирно закрепленной на ведущем звене. При движении ведущего звена в рабочем направлении (ω1, v1) собачка 3 упирается в зуб ведомого звена и перемещает его. При возвращении ведущего звена и собачки 3 в исходное положение храповое колесо (рейка) остается неподвижным. Фиксация ведомого звена обеспечивается трением в опорах звена, тормозом или стопорной собачкой 3′, нейтрализующих действие сил или моментов сил (Fc, Mc) полезного сопротивления. 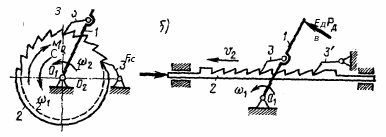  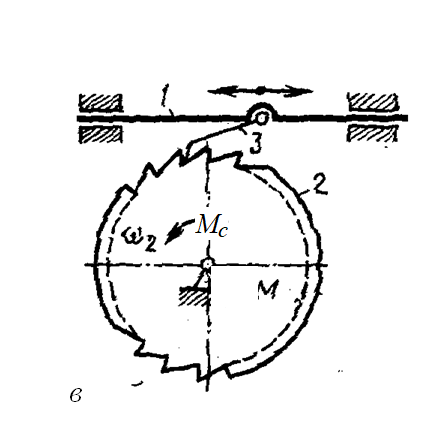 Рис 17.5 Храповые (зубчато-рычажные) механизмы применяют в устройствах транспортирования с прерывистым движением; в реле времени; шаговых искателях; механических и электрических часах и других устройствах. Зацепление собачки с ведомым звеном может быть внешним и внутренним. Большее распространение получили механизмы с внешним зацеплением как более простые по конструкции и изготовлению. Роль ведущего звена с собачкой храповых механизмов выполняют рабочие звенья других механизмов: шарнирного четырехзвенника (рис. 17.6, а), кулачкового (рис. 17.6, б), кривошипно-ползунного (рис. 17.6, в). В качестве исходных данных при проектировании храпового механизма задают габаритные размеры узла, угол поворота храпового колеса φ2 (см. рис. 17.6, а) за один ход собачки, момент сопротивления Мс. Число зубьев храпового колеса z определяется как z = 2π/ φ2. Количество зубьев на храповом колесе принимают равным 8 … 48, однако предпочтительнее z = 12 … 20. Основной параметр, модуль m, выбирают по заданному габаритному размеру, наружному диаметру D (рис. 17.7) храпового колеса m = D/z (17.10) Схема креста  Рисунок 1 – Основные размеры креста Количество пазов креста составило Z = 6 штук. Ширина пазов составила 1 см., глубина – 2 см. Минимальный радиус креста r2min = 3,5 см, максимальный r2max= 4 см. Межосевое расстояние а = 4,8 см. Изменение коэффициента движения мальтийского механизма от числа пазов креста
Таблица 1 – Зависимость коэффициента движения Кд от числа пазов креста Z Видно, что при наличии двух пазов не происходит зацепление, из-за чего движение невозможно и Кд =0.  График 1 – Зависимость коэффициента движения Кд от числа пазов креста Z Самые резкие изменения коэффициента движения наблюдаются при малых значениях числа пазов. Это связано с тем, что при добавлении одного паза окружность делится на большее число, что ведёт к меньшим углам между пазами, и в случае малых значениях числа пазов частное от деления изменяется сильнее, чем при больших значениях числа пазов. Изменение углового ускорения ε2 мальтийского механизма от числа пазов креста Z при неизменной скорости кривошипа (ω1 = 1)
Таблица 2 – Зависимость изменения углового ускорения ε2 мальтийского механизма от числа пазов креста Z при постоянной скорости кривошипа  График 2 – Изменение углового ускорения ε2 мальтийского механизма от числа пазов креста Z при неизменной скорости кривошипа (ω1 = 1) Малое число пазов предполагает большие значения углов между ними, и при сравнении с крестом с большим числом пазов видно, что в первом случае один паз отвечает за поворот диска на значительный угол. При одинаковой скорости вращения кривошипа, крест с малым числом пазов должен повернуться на больший угол, чем крест с малым числом пазов за одно и то же время. Также ускорение непостоянно при вращении креста и имеет максимумы примерно на середине паза (см. рис. 3). Таким образом, механизмы с малым числом пазов совершают движения с большим ускорением, чем механизмы с малым числом пазов за одинаковые промежутки времени. При большом количестве пазов разница между количеством пазов становится не так заметна, так как и угол между пазами уменьшается на незначительные величины.  График 3 – Изменение угловой скорости ω и углового ускорения ε от угла поворота кривошипа Выводы Мальтийские механизмы служат для преобразования равномерного вращательного движения ведущего звена (кривошипа) в периодические повороты с остановками ведомого звена, креста. В данной лабораторной работе были рассмотрены механизмы различной конфигураций для определения зависимостей коэффициента движения и углового ускорения от числа пазов мальтийского креста. Было выяснено, что коэффициент движения растёт почти пропорционально числу пазов креста. Угловое ускорение уменьшается с ростом числа пазов, при этом график изменения похож на гиперболу. Эти механизмы в сочетании с зубчатыми передачами используют для прерывистого движения лент, автоматах и других механизмов. Список использованных источников Сурин В.М. Прикладная механика, Новое знание, 2005. Белов М.И., Сорокин С.В. К расчету мальтийского механизма // Universum: технические науки : электрон. научн. журн. 2017 |
