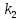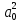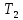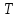ИТМО робастное управление. Лабораторная работа 4 синтез дискретных стабилизирующих алгоритмов управления вариант 2 Выполнили студенты гр. R3440 Рекин В. И
 Скачать 101.6 Kb. Скачать 101.6 Kb.
|
|
Университет ИТМО Факультет систем управления и робототехники Лабораторная работа №4 СИНТЕЗ ДИСКРЕТНЫХ СТАБИЛИЗИРУЮЩИХ АЛГОРИТМОВ УПРАВЛЕНИЯ Вариант 2 Выполнили: студенты гр. R3440 Рекин В.И. Федорова Г.Д. Проверил: Чепинский С.А. Санкт-Петербург 2021г. Цель работы Ознакомление с принципами синтеза дискретных регуляторов систем автоматического управления, работающих в режиме стабилизации. Исходные данные Исходные данные представлены в таблице 1. Таблица 1 - Параметры ОУ
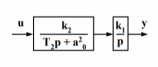 Рисунок 1 - Вид объекта управления Порядок выполнения работы Для заданного ОУ получим модель в пространстве состояний: Вычислим передаточную функцию 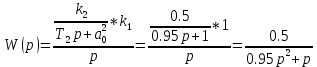 Модель вход-выход: 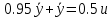 Векторно-матричная форма полученной модели: 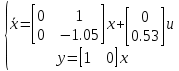 где x — вектор состояния; u — управляющее воздействие; y — выходная или регулируемая переменная. Осуществим переход к дискретному описанию ОУ Воспользуемся формулами: 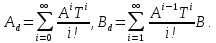 Полученные матрицы: 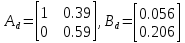 Произведем моделирование непрерывного и дискретного объектов. Графики переходных процессов представлены на рисунке 2. 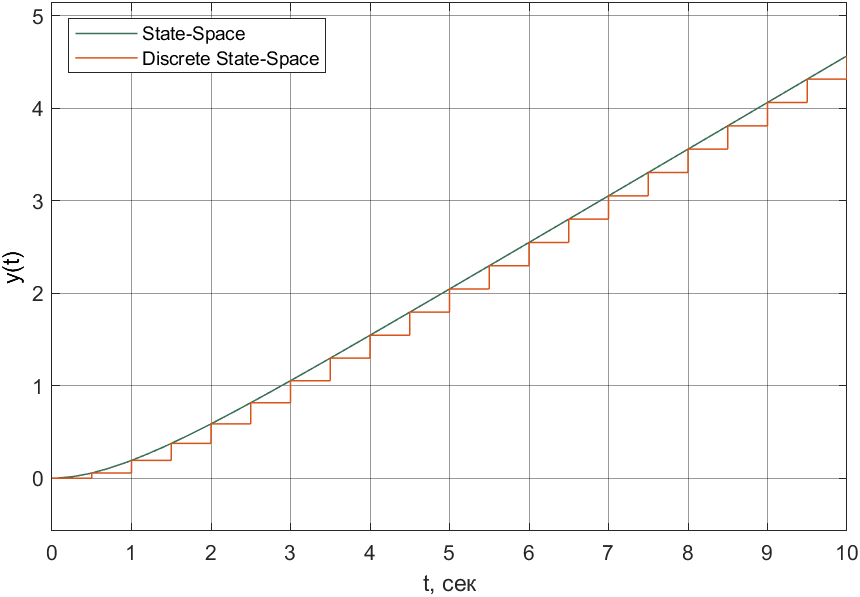 Рисунок 2 – Переходные процессы По полученным графикам видно, что полученная дискретная система приближена к исходной. Произведем проверку ОУ на полную управляемость Сформируем матрицу управления в виде 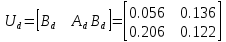 Определитель матрицы 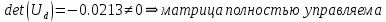 . .устойчивость Чтобы проверить систему на устойчивость приравняем характеристический полином к 0 и найдем его корни: 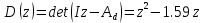 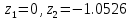 Так как один из корней характеристического полинома равен 1, система находится на границе устойчивости. Построим эталонную модель для корней оптимальной дискретной системы по быстродействию, то есть 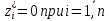 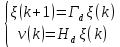 Матрицы 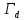 и и 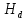 формируются в соответствии с требуемыми показателями качества. Из условия все корни характеристического полинома вещественные и одинаковые формируются в соответствии с требуемыми показателями качества. Из условия все корни характеристического полинома вещественные и одинаковые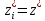 , имеем матрицы: , имеем матрицы: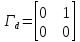 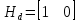 Теперь определим требуемый характеристический полином: 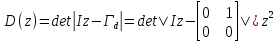 Вычислим коэффициенты обратных связей: 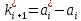 Найдем 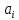 Передаточная функция дискретной системы: 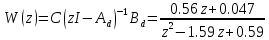 Сформируем канонически управляемую модель дискретного ОУ: 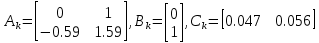 Сформируем матрицу управляемости канонически управляемой модели дискретного ОУ: 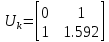 Определитель матрицы управляемости равен -1, значит, пара матриц полностью управляема. Тогда матрица преобразования М находится в следующем виде: 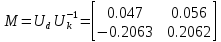 Найдем матрицу линейных стационарных обратных связей. Из матрицы 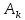 : :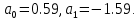 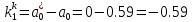 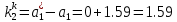 Матрица линейных стационарных обратных связей в канонически управляемом базисе имеет вид: 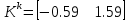 Теперь найдем матрицу линейных стационарных обратных связей в исходном базисе: 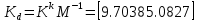 Вычислим матрицу замкнутой системы, воспользовавшись формулой: 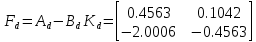 И найдем дискретный характеристический полином замкнутой системы: 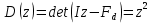 Полученный полином совпадает с желаемым характеристическим полиномом, а значит синтез системы проведен верно. Промоделируем полученную замкнутую систему при начальных условиях 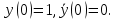 Схема моделирования и результаты представлены на рисунках 3 и 4. Схема моделирования и результаты представлены на рисунках 3 и 4.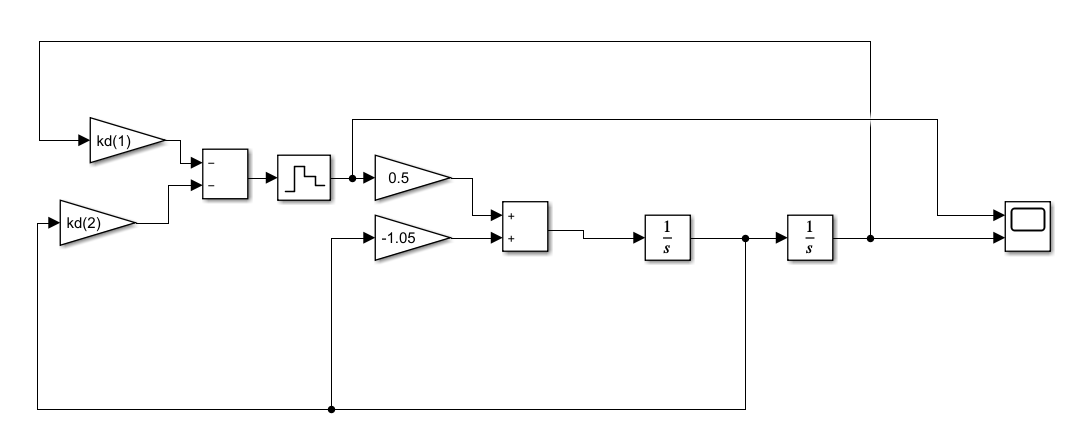 Рисунок 3 – Схема моделирования 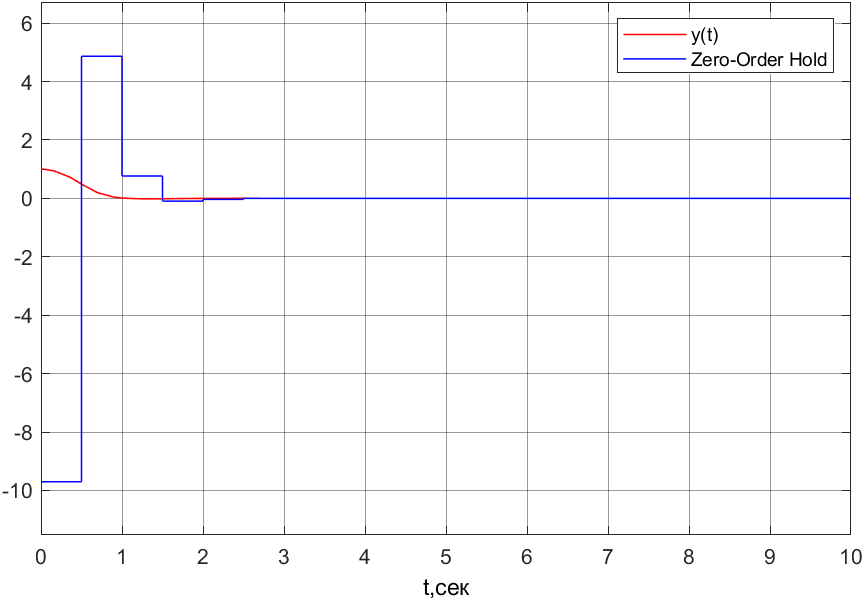 Рисунок 4 – График переходных характеристик В результате синтеза управляющих воздействий было получено желаемое поведение системы. Вывод В ходе выполнения данной лабораторной работы был синтезирован дискретный регулятор, работающий в режиме стабилизации. По заданной передаточной функции было восстановлено дифференциальное уравнение системы, на его основе был осуществлен переход к непрерывной модели вход-состояние-выход, а затем к её дискретному представлению. Проверка на адекватность перехода прошла успешно. Далее провели проверку системы на управляемость и устойчивость, в результате получили, что данная система является полностью управляемой и неустойчивой. В результате моделирования регулятора, работающего в режиме стабилизации, получили так же неустойчивую систему. Предполагаем, что устойчивость исходной системы влияет на возможность осуществления стабилизации. Если исходная система неустойчива, то привести её к устойчивой эталонной модели не удастся. |