Лабораторная работа 4к определение момента инерции махового колеса методом колебаний. Казань 2002

• Название: Лабораторная работа 4к определение момента инерции махового колеса методом колебаний. Казань 2002
• Дата: 23.05.2023
• Размер: 359.5 Kb.
• Имя файла: 4К.doc
• Тип: Лабораторная работа; #1154976

Министерство образования Российской Федерации
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени А.Н. Туполева
Кафедра общей физики

Лабораторная работа №4К
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА МЕТОДОМ КОЛЕБАНИЙ.

Казань 2002


Цель работы: изучение метода колебаний и определение момента инерции махового колеса.
ОСНОВНОЕ УРАВНЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Вращательное движение материальной точки характеризуется следующими величинами : углом поворота , угловой скоростью и угловым ускорением .

При вращательном движении результат действия сил на тело определяется действующим на него моментом силы М и зависит от момента инерции J тела. Произведение момента инерции тела на его угловое ускорение численно равно результирующему моменту сил, действующих на это тело :

M=  J . (1)
Cоотношение (1) называется основным уравнением динамики вращательного движения.

Моментом силы относительно оси называется вектор, направленный вдоль оси, численно равный произведению силы на плечо, если сила действует в плоскости, перпендикулярной оси вращения.

Моментом инерции J материальной точки относительно оси вращения называется произведение массы m точки на квадрат расстояния r до оси вращения

J=mr². (2)
Момент инерции любого тела равен сумме моментов инерции составляющих его материальных точек

J= , (3)
где N - число частиц, на которое разбито тело; m_i и r_i - масса и расстояние от точки до оси вращения.

Момент инерции тел во воащательном движении выполняет роль, аналогичную роли массы в поступательном движении. Как масса, так и момент инерции являются мерой инертности .

Для однородных тел простой формы момент инерции относительно оси симметрии может быть рассчитан аналитически. Например, момент инерции плоского диска или сплошного цилиндра относительно геометрической оси симметрии равен

J= ,

где m - масса диска или цилиндра, r - радиус диска или цилиндра.

Момент инерции шара относительно оси, совпадающей с любым из его диаметров, вычисляется так:

J= ,

где m и r - масса и радиус шара.

Момент инерции тела относительно любой оси может быть рассчитан по теореме Штейнера, которая формулируется следующим образом : момент инерции J тела относительно произвольной оси равен сумме момента инерции J₀ этого тела относительно оси, проходящей через центр тяжести параллельно данной оси, и произведения массы тела m на квадрат расстояния d между осями :

J=J₀+md² .

(4)

Кинетическая энергия вращающегося относительно неподвижой оси тела также зависит от момента инерции его :

W_кин= .

(5)

Работа при вращении твердого тела равна

А=М ,

(6)

где М - вращающий момент силы, - угол поворота под действием момента М.

Когда во время движения тела момент инерции его изменяется, основное уравнение динамики вращательного движения должно быть записано в более общей форме:

. (7)
Величина J называется моментом количества движения. Из уравнения (7) как следствие вытекает закон сохранения момента количества движения. Если суммарный момент, действующий на тело или систему тел, равен нулю, то момент количества движения этого тела или системы тел остается неизменным, т.е. если М=0, то L= const.

При сложной геометрической форме тела аналитический подсчет его момента инерции провести трудно. В этих случаях его определяют экспериментально.

Описание установки и вывод рабочей формулы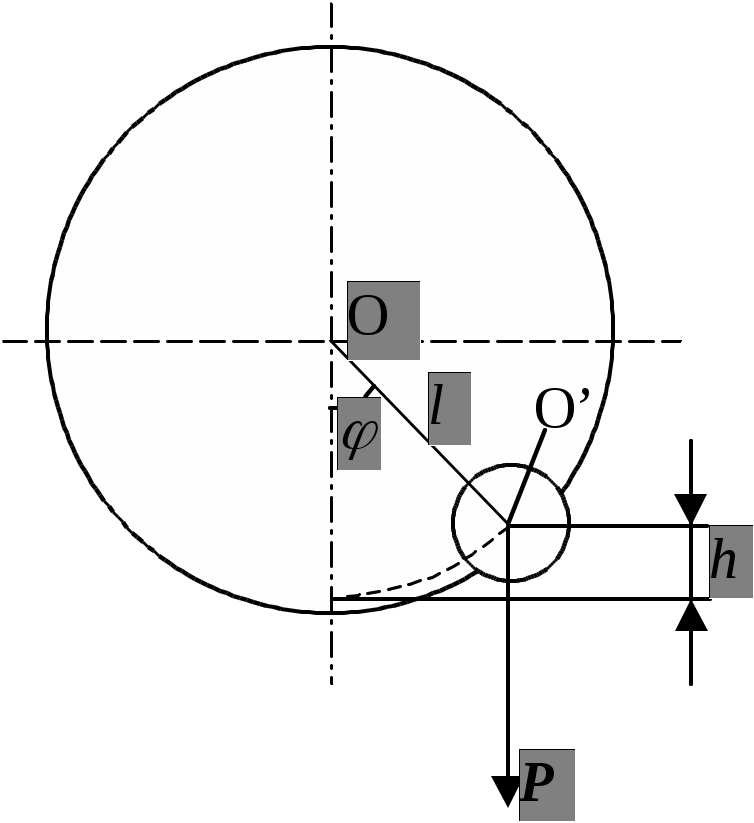

Рис. 1.

Определение момента инерции махового колеса методом колебаний производят следующим образом. К ободу колеса прикрепляют некоторый груз весом Р (рис.1). Колесо выводят из положения равновесия и затем отпускают. Система начинает совершать колебания, которые при достаточно малых углах отклонения можно считать гармоническими. Так как ось вращения проходит через центр тяжкести колеса, то при отклонении груза от положения равновесия потенциальная энергия системы равна потенциальной энергии груза Р , поднятого на высоту h:

W_пот=mgh, (7)
где m- масса груза. При прохождении положения равновесия эта энергия полностью переходит в кинетическую энергию колеса и груза. Следовательно, можем записать

W_kин=

где J- момент инерции всей системы относительно оси вращения О, - угловая скорость системы в момент прохождения положения равновесия.

Запишем закон сохранения энергии

mgh= . (8)
Так как h и непосредственно измерить трудно, выразим их через другие измеряемые величины. Из рис.1. видно, что

h=L(1-cos )=2L sin²
Синусы малых углов можно заменять самими углами в радианах, поэтому sin² . Тогда . При гармонических колебаниях угловое смещение определяется формулой

sin ,

где -амплитуда колебаний; Т- период колебаний .Угловая скорость равна

cos .

Подставляя выражения для h и амплитудного значения угловой скорости в (8), получим:

Т=2 . (9)

Эта формула определяет период физического маятника.

Момент инерции J системы равен сумме момента инерции колеса и момента инерции J₁добавочного груза относительно оси вращения системы

J₁=J₀+J₁ (10)

Момент инерции груза относительно оси вращения системы согласно теореме Штейнера определяется так:

J₁=J₀₁+mL², (11)
где J_0l- момент инерции груза относительно оси О^/ , проходящей через центр тяжести груза, параллельно оси О; L- расстояние между осями.Если добавочный груз имеет форму цилиндра, геометрическая ось которого расположена параллельно оси О, то

J₀₁= , (12)
где r- радиус груза.

С учетом (10)-(12) уравнение (9) можно переписать в виде

Т²= . (13)
Из (13) находим момент инерции колеса

J₀= . (14)
Для определения момента инерции махового колеса методом колебаний по формуле (14) необходимо измерить массу m и радиус r груза, расстояние L от центра тяжести груза до оси вращения и период гармонических колебаний колеса с грузом Т.

Порядок выполнения работы

1. 
   Начертить в тетради таб. 1.
   

Табл.1

№ измерен.	m	n	t	Tср	L	r	J0
1. 2. 3. 4. 5.

2. 
   Запустить программу 4К.ЕХЕ. Для этого указать курсором на 4К.ЕХЕ и щелкнуть левой кнопкой мыши (в дальнейшем эту команду обозначим L’ на 4К.ЕХЕ). Изучить информацию на экране.
   

3. 
   Задать значения массы груза m, расстояния между осями L и радиус груза r.
   

4.L’ на команде «Обновить» 4.

5. Нажать левой кнопкой мышки на груз и не отпуская установить угол отклонения груза.

6. L’ на Начать.

7. L’ на Зафиксировать время 10 колбаний.

8. L’ на Зафиксировать время 20 колбаний.

9. Повторить пункты 5-8 еще 4 раза.

10. L’ на калькуляторе и вычислить значения Т₁₀, Т₂₀, Т_ср, J₀.

11. Вычислить средний момент инерции по формуле:

J_ср= .

12. Вычислить абсолютную и относительную ошибки измерений.

13. Данные таблицы переписать в тетрадь.

14. Закрыть программу 4К.ЕХЕ.
Контрольные вопросы и задания.

1. Сформулируйте теорему Штейнера.

2. Приведите вывод рабочей формулы.

3. Как вычисляются моменты инерции цилиндра ?