лабораторная работа 7.1 сибгути. Лабораторная работа 7. 1 определение длины электромагнитной волны с помощью бипризмы френеля студент гр. Ап103 Гальцев Е
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
|
Федеральное агентство связи СибГУТИ Кафедра физики Лабораторная работа №7.1 «ОПРЕДЕЛЕНИЕ ДЛИНЫ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ С ПОМОЩЬЮ БИПРИЗМЫ ФРЕНЕЛЯ» Выполнил: студент гр. АП-103 Гальцев Е. Бригада 5 Преподаватель: Сундукова М.С.  ЦЕЛЬ РАБОТЫ Ознакомиться с явлением интерференции света. Методом бипризмы Френеля определить длину электромагнитной волны видимого диапазона. 2) Краткая теория Существует ряд явлений, в которых свет ведёт себя как поток частиц (фотонов). Однако такие явления, как интерференция, дифракция, поляризация и дисперсия света, которые изучаются в данном лабораторном практикуме, могут быть объяснены только на основе волновых представлений. Таким образом, свет обнаруживает корпускулярно-волновой дуализм: в одних явлениях проявляется его волновая природа, и он ведёт себя как электромагнитная волна, в других явлениях проявляется корпускулярная природа света, и он ведёт себя как поток фотонов. Плоская монохроматическая (синусоидальная) электромагнитная волна, распространяющаяся в нейтральной непроводящей среде с постоянными проницаемостями ε и μ (ρ=0, j=0, ε=const, μ=const) описывается функциями (см. рис.1): 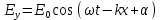 (1) (1) Где: 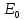 – амплитуда напряжённости электрического поля в волне; – амплитуда напряжённости электрического поля в волне; – амплитуда напряжённости магнитного поля в волне: – амплитуда напряжённости магнитного поля в волне: – циклическая частота; – циклическая частота; λ – длина волны; t – время; x – координата, совпадающая с направлением распространения волны, расстояние от источника до данной точки; α – начальная фаза колебаний в точке с координатой x = 0. Колебания векторов напряженности электрического E и магнитного H полей в электромагнитной волне происходят в одной фазе, а их амплитуды однозначно связаны между собой формулой:  . Поэтому принято описывать такую волну лишь с помощью вектора . Поэтому принято описывать такую волну лишь с помощью вектора  , который иногда называется световым вектором. , который иногда называется световым вектором.При прохождении двух или нескольких электромагнитных волн через среду может сложиться ситуация, когда колебания напряжённостей электрического и магнитного полей разных волн в одних точках пространства будут усиливать друг друга, а в других ослаблять. Это явление называется интерференцией. В случае электромагнитных волн видимого диапазона вследствие интерференции происходит перераспределение светового потока в интерференционном поле, приводящее к появлению в одних местах максимумов интенсивности излучения, а в других – минимумов.  Рисунок 1 – строение плоской электромагнитной волны Необходимым условием наблюдения интерференции является когерентность волн, что означает согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. При этом разность фаз колебаний в данной области пространства во все время наблюдения остается постоянной. Этому условию удовлетворяют монохроматические (синусоидальные) волны одинаковой частоты и одинакового направления колебаний вектора  (одинаковой поляризации). (одинаковой поляризации).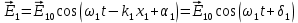 (2) (2)  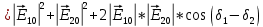 (3) (3)Если разность фаз  , возбуждаемых волнами с одинаковой частотой ω, остаётся постоянной во времени, то волны , возбуждаемых волнами с одинаковой частотой ω, остаётся постоянной во времени, то волныназываются когерентными. Существуют понятия пространственной и временной когерентности. Временная когерентность связана разбросом значений модуля волнового вектора  . .Поскольку интенсивность световой волны пропорциональна квадрату амплитуды напряжённости электрического поля волны, то формулу (3) можно переписать в виде:  (4) (4)Для когерентных волн интерференционный член в (4) 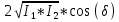 не равен нулю в среднем по времени. Потребуем, чтобы α1 = α2, тогда: не равен нулю в среднем по времени. Потребуем, чтобы α1 = α2, тогда:  (5) (5)где  и и 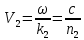 – фазовые скорости волн, с – скорость света в вакууме. Назовём величину Δ=n2x2 – фазовые скорости волн, с – скорость света в вакууме. Назовём величину Δ=n2x2  n1x1 =L2 n1x1 =L2  L1 оптической разностью хода двух лучей, величину L1 = n1x1 оптической длиной пути первого луча из S1 до точки М. Подставляем в (5), получаем: L1 оптической разностью хода двух лучей, величину L1 = n1x1 оптической длиной пути первого луча из S1 до точки М. Подставляем в (5), получаем: (6) (6)где  – длина волны в вакууме. Из (4) видно, что если разность фаз равна чётному числу π, то есть δ = + 2π * m, где m = 0, 1, 2, …, то интерференционный член в (4) будет равен 2 – длина волны в вакууме. Из (4) видно, что если разность фаз равна чётному числу π, то есть δ = + 2π * m, где m = 0, 1, 2, …, то интерференционный член в (4) будет равен 2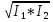 , интенсивность I будет максимальной. Напротив, если разность фаз будет равна нечётному числу π, то есть, , интенсивность I будет максимальной. Напротив, если разность фаз будет равна нечётному числу π, то есть, 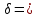   , где m = 0, 1, 2, …, то интерференционный член в (4) будет равен –2 , где m = 0, 1, 2, …, то интерференционный член в (4) будет равен –2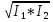 , интенсивность I будет минимальной. , интенсивность I будет минимальной.3) Описание экспериментальной установки Установка состоит из источника света «И», щели «S», бипризмы «Б», измерительного микроскопа «М» с экраном «Э», линзы и светофильтра (рис. 2). Линза и светофильтр на рисунке не показаны. Все вышеуказанные приборы крепятся на оптической скамье.  Рисунок 2 – схема лабораторной установки.  Рисунок 3 – описание лабораторной установки. 4. Выполнение Таблица №1
 l 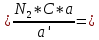 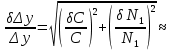   Δλ = λрас * σ = λ = λрас ± Δλ = Вывод: во время выполнения лабораторной работы 7.1 я определил длину электромагнитной волны видимого диапазона, она равна 678 нм, а также относительную и абсолютную погрешности измерений (  и 187 нм соответственно). и 187 нм соответственно).6. Контрольные вопросы  6.1) Cвет обнаруживает корпускулярно-волновой дуализм (двойственность): в одних явлениях проявляется его волновая природа, и он ведёт себя как электромагнитная волна, в других явлениях проявляется корпускулярная природа света, и он ведёт себя как поток фотонов. Плоская монохроматическая (синусоидальная) электромагнитная волна, распространяющаяся в нейтральной непроводящей среде с постоянными значениями электрической и магнитной проницаемости (ε = const, = const), описывается функциями   6.2) При прохождении двух или нескольких электромагнитных волн через среду может сложиться ситуация, когда колебания напряжённостей электрического и магнитного полей разных волн в одних точках пространства будут усиливать друг друга, а в других ослаблять. Это явление называется интерференцией. Примеры: мыльные пузыри, радуга, топливные капли в лужах. 6.3) Что регистрируют наши глаза и приборы при попадании в них электромагнитных волн? III) Человеческий глаз регистрирует электромагнитные волны длиной приблизительно от 380 до 760 нм (такие волны называют видимым светом). Фотохимические процессы в сетчатке глаза заключаются в том, что находящийся в наружных члениках палочек зрительный пурпур (родопсин) разрушается под действием света и восстанавливается в темноте. Действие света не объясняется лишь исключительно фотохимической реакцией. При попадании света на сетчатку в зрительном нерве возникают токи действия, фиксируемые высшими центрами коры головного мозга. Фотодиод представляет собой полупроводниковый диод, в котором обеспечивается возможность воздействия оптического излучения на р–n-переход. При воздействии потока света на плоскость перехода фотоны поглощаются с энергией, превышающей предельную величину, поэтому в n-области образуются пары носителей заряда – фотоносители. При этом повышается обратный ток фотодиода. 6.4) Когерентность волн – согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов с одинаковой частотой колебания. При этом разность фаз колебаний в данной области пространства во все время наблюдения остается постоянной. Этому условию удовлетворяют монохроматические (синусоидальные) волны одинаковой частоты. Необходимым условием наблюдения интерференции является когерентность волн, что означает согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Временная когерентность – когерентность колебаний, которые совершаются в одной и той же точке пространства в разные моменты времени и связана с разбросом волнового вектора по величине. Пространственная когерентность – это когерентность колебаний, которые совершаются в один и тот же момент времени в различных точках пространства и связана с разбросом волнового вектора по направлению. 6.5)  (4) (4)Для когерентных волн интерференционный член в (4) 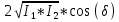 не равен нулю в среднем по времени. Потребуем, чтобы α1 = α2, тогда: не равен нулю в среднем по времени. Потребуем, чтобы α1 = α2, тогда:  (5) (5)где  и и 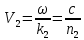 – фазовые скорости волн, с – скорость света в вакууме. Назовём величину Δ=n2x2 – фазовые скорости волн, с – скорость света в вакууме. Назовём величину Δ=n2x2  n1x1 =L2 n1x1 =L2  L1 оптической разностью хода двух лучей, величину L1 = n1x1 оптической длиной пути первого луча из S1 до точки М. Подставляем в (5), получаем: L1 оптической разностью хода двух лучей, величину L1 = n1x1 оптической длиной пути первого луча из S1 до точки М. Подставляем в (5), получаем: (6) (6)где  – длина волны в вакууме. Из (4) видно, что если разность фаз равна чётному числу π, то есть δ = + 2π * m, где m = 0, 1, 2, …, то интерференционный член в (4) будет равен 2 – длина волны в вакууме. Из (4) видно, что если разность фаз равна чётному числу π, то есть δ = + 2π * m, где m = 0, 1, 2, …, то интерференционный член в (4) будет равен 2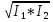 , интенсивность I будет максимальной. Напротив, если разность фаз будет равна нечётному числу π, то есть, , интенсивность I будет максимальной. Напротив, если разность фаз будет равна нечётному числу π, то есть, 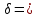   , где m = 0, 1, 2, …, то интерференционный член в (4) будет равен –2 , где m = 0, 1, 2, …, то интерференционный член в (4) будет равен –2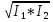 , интенсивность I будет минимальной. , интенсивность I будет минимальной.Подставляя последние условия в (6), получаем условия максимума и минимума интенсивности интерференционной картины:  6.6) Бипризма Френеля — оптическое устройство для получения когерентных световых пучков, созданное Огюстеном Френелем. Бипризма представляет собой две одинаковых треугольных прямоугольных призмы, с очень малым преломляющим углом, сложенные своими основаниями. Для получения интерференции источник света S располагают симметрично относительно бипризмы. Углы падения лучей на поверхности призмы малы, поэтому все лучи отклоняются ею на практически одинаковый угол  , где n – показатель преломления бипризмы, из которого изготовлена призма, а Θ – преломляющий угол призмы. , где n – показатель преломления бипризмы, из которого изготовлена призма, а Θ – преломляющий угол призмы.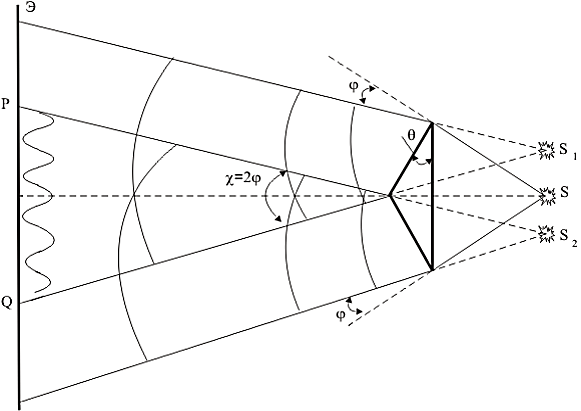 Рисунок 6 – поле интерференции света. В результате образуются два когерентных пучка света, вершины которых S1 и S2 можно рассматривать, как точки расположения мнимых изображений источника S. На экране когерентные лучи от источников S1 и S2 перекрываются и формируют интерференционную картину, представляющую собой набор чередующихся между собой светлых и тёмных полос. Апертура перекрывающихся световых пучков (χ = 2φ) – это угол, в области которого образуется интерференционная картина. 6.7) Найдём аналитическое выражение для определения длины волны λ. Пусть экран «Э» расположен нормально к оси симметрии (SM) измерительной установки (рис. 7). Пусть в точке Z экрана наблюдается интерференционный максимум от двух плоских когерентных волн, распространяющихся из двух источников S1 и S2 вдоль направлений [S1Z) и [S2Z). Оптическая разность хода между лучами [S1Z) и [S2Z) в точке Z в случае, если экран расположен достаточно далеко от источников и при  , то: , то: , где n – абсолютный показатель преломления среды, в которой распространяются волны. , где n – абсолютный показатель преломления среды, в которой распространяются волны. l l  Рисунок 7 – схема интерференции от двух источников. При l << L можно считать, что sinβ ≈ tg β ≈ β и  x ≈ l * β; x ≈ l * β;r ≈ L * β; (1) И (2) Для максимумов различных порядков m и k имеем: ( Согласно условию максимумов интенсивности интерференционной картины:   (4) (4)Подставляя (4) в (3), можно определить расстояние от центра экрана до максимума произвольного порядка. Вычитая уравнения (3) почленно, получаем: Подстановка (4) в (3) даёт: Р (5) Получим из (5) длину электромагнитной волны: 6.8) При введении линзы «Л» нарушается когерентность волн, то есть через линзу проходят некогерентные волны, поэтому интерференционная картина на экране "разрушается". 6.9) В начале эксперимента не применялся ни один светофильтр, при этом наблюдалось чередование тёмных и светлых полос. То есть, изначально световая волна была полихромной. После введения красного светофильтра вместо светлых полос появились светло-красные полосы, то есть световая волна стала монохромной. В ходе эксперимента были сделаны замеры, благодаря которым стало возможным рассчитать длину световой волны. Она оказалось равной 678 нм, что соответствует красному диапазону длин волн. 6.10) Мы можем четко наблюдать интерференционные максимумы при m << mкр. Отсюда следует, что число доступных наблюдению интерференционных максимумов возрастает с уменьшением интервала длин волн, представленном в световом потоке. То есть число интерференционных полос на экране зависит от степени монохроматичности света. Для получения интерференционной картины путем деления естественной волны на две части необходимо, чтобы оптическая разность хода была меньше, чем длина когерентности: Δког << lког, или:  Это требование ограничивает число видимых интерференционных полос. |
