laboratornaya-rabota-78-отчет. Лабораторная работа 7 Создание макросов в Excel Цель работы Ознакомиться со способами создания и использования макросов
 Скачать 40.23 Kb. Скачать 40.23 Kb.
|
|
Лабораторная работа № 7 Создание макросов в Excel Цель работы: Ознакомиться со способами создания и использования макросов. Задание на выполнение работы: создать макросы с использованием Excel Порядок выполнения работы: Вариант 20 Дана следующая матрица выигрышей: 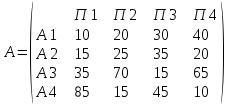 Определите оптимальную стратегию используя критерии Вальда, Сэвиджа и Гурвица (коэффициент пессимизма равен 0,5). Решение: Критерий Байеса. По критерию Байеса за оптимальные принимается та стратегия (чистая) Ai, при которой максимизируется средний выигрыш a или минимизируется средний риск r. Считаем значения ∑(aijpj) ∑(a1,jpj) = 10*0.25 + 20*0.25 + 30*0.25 + 40*0.25 = 25 ∑(a2,jpj) = 15*0.25 + 25*0.25 + 35*0.25 + 20*0.25 = 23.75 ∑(a3,jpj) = 37*0.25 + 70*0.25 + 15*0.25 + 65*0.25 = 46.75 ∑(a4,jpj) = 85*0.25 + 15*0.25 + 45*0.25 + 10*0.25 = 38.75
Выбираем из (25; 23.75; 46.75; 38.75) максимальный элемент max=46.75 Вывод: выбираем стратегию N=3. Критерий Вальда. По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е. a = max(min aij) Критерий Вальда ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
Выбираем из (10; 15; 15; 10) максимальный элемент max=15 Вывод: выбираем стратегию N=2. Критерий Севиджа. Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается: a = min(max rij) Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации. Находим матрицу рисков. Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце bj = max(aij) характеризует благоприятность состояния природы. 1. Рассчитываем 1-й столбец матрицы рисков. r11 = 85 - 10 = 75; r21 = 85 - 15 = 70; r31 = 85 - 37 = 48; r41 = 85 - 85 = 0; 2. Рассчитываем 2-й столбец матрицы рисков. r12 = 70 - 20 = 50; r22 = 70 - 25 = 45; r32 = 70 - 70 = 0; r42 = 70 - 15 = 55; 3. Рассчитываем 3-й столбец матрицы рисков. r13 = 45 - 30 = 15; r23 = 45 - 35 = 10; r33 = 45 - 15 = 30; r43 = 45 - 45 = 0; 4. Рассчитываем 4-й столбец матрицы рисков. r14 = 65 - 40 = 25; r24 = 65 - 20 = 45; r34 = 65 - 65 = 0; r44 = 65 - 10 = 55;
Результаты вычислений оформим в виде таблицы.
Выбираем из (75; 70; 48; 55) минимальный элемент min=48 Вывод: выбираем стратегию N=3. Проведение идеального эксперимента. В крайнем правом столбце рассчитаем средний риск.
Минимальное значение средних рисков равно 0. Следовательно, выше этой цены планирование эксперимента становится нецелесообразным. Критерий Гурвица. Критерий Гурвица является критерием пессимизма - оптимизма. За оптимальную принимается та стратегия, для которой выполняется соотношение: max(si) где si = y min(aij) + (1-y)max(aij) При y = 1 получим критерий Вальде, при y = 0 получим – оптимистический критерий (максимакс). Критерий Гурвица учитывает возможность как наихудшего, так и наилучшего для человека поведения природы. Как выбирается y? Чем хуже последствия ошибочных решений, тем больше желание застраховаться от ошибок, тем y ближе к 1. Рассчитываем si. s1 = 0.5*10+(1-0.5)*40 = 25 s2 = 0.5*15+(1-0.5)*35 = 25 s3 = 0.5*15+(1-0.5)*70 = 42.5 s4 = 0.5*10+(1-0.5)*85 = 47.5
Выбираем из (25; 25; 42.5; 47.5) максимальный элемент max=47.5 Вывод: выбираем стратегию N=4. Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A3. Множество Парето
ME(1)=10*0.25+20*0.25+30*0.25+40*0.25=25=25 σ(1)=sqrt(102*0.25+202*0.25+302*0.25+402*0.25-252) = sqrt(125)=11.18
ME(2)=15*0.25+25*0.25+35*0.25+20*0.25=23.75=23.75 σ(2)=sqrt(152*0.25+252*0.25+352*0.25+202*0.25-23.752) = sqrt(54.69)=7.395
ME(3)=37*0.25+70*0.25+15*0.25+65*0.25=46.75=46.75 σ(3)=sqrt(372*0.25+702*0.25+152*0.25+652*0.25-46.752) = sqrt(494.19)=22.23
ME(4)=85*0.25+15*0.25+45*0.25+10*0.25=38.75=38.75 σ(4)=sqrt(852*0.25+152*0.25+452*0.25+102*0.25-38.752) = sqrt(892.19)=29.87 Критерии оптимизации: x → max y → min Операция №3 доминирует над №4. 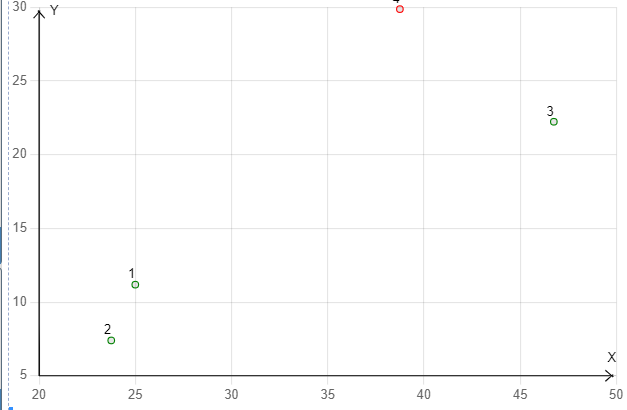 Операция №3 доминирует над №4. Следовательно, операции №3, оптимальны по Парето. Операции, оптимальные по Парето, не обязательно являются «самыми лучшими» и даже просто «хорошими» - эти операции не являются худшими. Контрольные вопросы В чем состоит отличительная особенность принятия решения в игре с «природой»? Ответ: Отличительная особенность игры с природой состоит в том, что в ней сознательно действует только один из участников, в большинстве случаев называемый игроком один. Игроку два (природа) не важен результат, либо он не способен к осмысленным решениям. Или, возможно, условия не зависят от действий игрока, а определяются внешними факторами: реакция рынка, который не будет вредить одному конкретному игроку, государственная политика, реальная природа. Специфика мажорирования стратегий в игре с природой? Ответ: Мажорирование стратегий в игре с природой имеет определенную специфику: исключить из рассмотрения можно лишь доминируемые стратегии игрока 1: если для всех j = 1,…n; akj ≤ alj; k u l = 1,..,m то k-ю стратегию принимающего. 36. решения игрока 1 можно не рассматривать и вычеркнуть из матрицы игры. Столбцы, отвечающие стратегиям природы, вычеркивать из матрицы игры (исключать из рассмотрения) недопустимо, поскольку природа не стремится к выигрышу в «игре» с человеком, она действует неосознанно, но иногда значения выигрышей лица, принимающего решение (ЛПР) не всегда располагаются по строкам Опишите два способа задания матрицы игры с природой. 1.Задачи о принятии решений в условиях неопределенности, когда нет возможности получить информацию о вероятностях появления состояний природы 2.Задачи о принятии решений в условиях риска, когда известны вероятности, с которыми природа принимает каждое из возможных состояний |
