Омпс. ОМПС лаба на сдачу. Лабораторная работа по дисциплине основы механики подвижного состава
 Скачать 3.08 Mb. Скачать 3.08 Mb.
|
4.3 Разработка основной системы для расчета методом силОбычно основную систему получают из заданной путем разрезания контуров рамы. В этих сечениях прикладывают внутренние силы (моменты) X – неизвестные метода сил. Далее раскрывают статическую неопределимость, находят значения X всех внутренних сил в системе, а по ним – значения напряжений. Разрежем раму тележки по центральной продольной оси (рисунок 8) и отсечем ближнюю к нам часть. Оставшуюся дальнюю часть развернем на 180°. Для соблюдения принципа геометрической неизменяемости заделываем правую концевую балку в месте разреза. Кроме того, если в месте разреза приложена сила, то эта сила делится пополам. 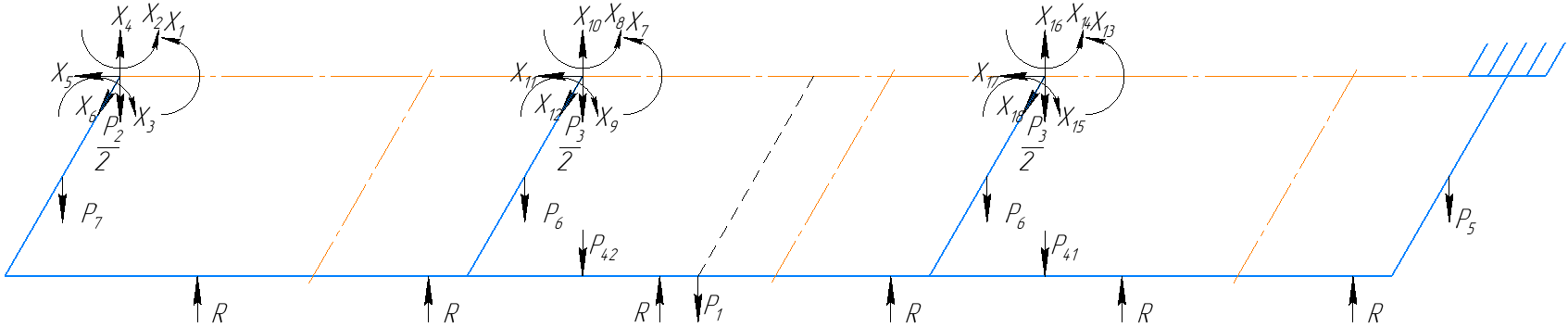 Рисунок 8 – Рама тележки, разрезанная по центральной продольной оси В общем случае в месте разреза получим 6 неизвестных метода сил. Однако, поскольку в данном случае приложена только вертикальная нагрузка, то внутренние силы в системе появятся также в вертикальном направлении. Поэтому X2, X5, X6, X8, X11, X12, X14, X17, X18 = 0. Кроме того, так как рама тележки рассчитывается на изгиб, то будем находить неизвестные изгибающие моменты X1, X7 и X13. Вертикальными составляющими X4, X10 и X16 и вертикальными моментами X3, X9 и X15 обычно пренебрегают и в расчете не учитывают, так как они вносят незначительный вклад в общую картину распределения напряжений. С учетом этого окончательно получим вид основной системы, при этом изгибающие моменты X1, X7 и X13 представим как X1, X2 и X3 (рисунок 9). 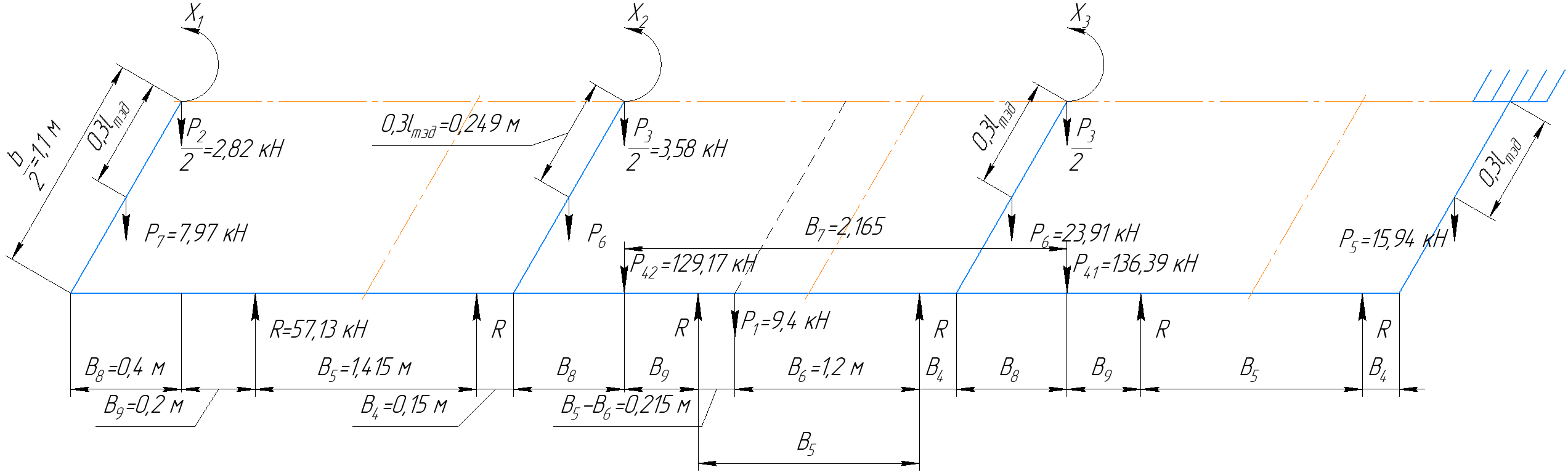 Рисунок 9 – Окончательный вид основной системы 4.4 Построение эпюр единичных моментовПостроим эпюры от действия безразмерных единичных моментов X1, X2, X3. 1) Воздействие X1. 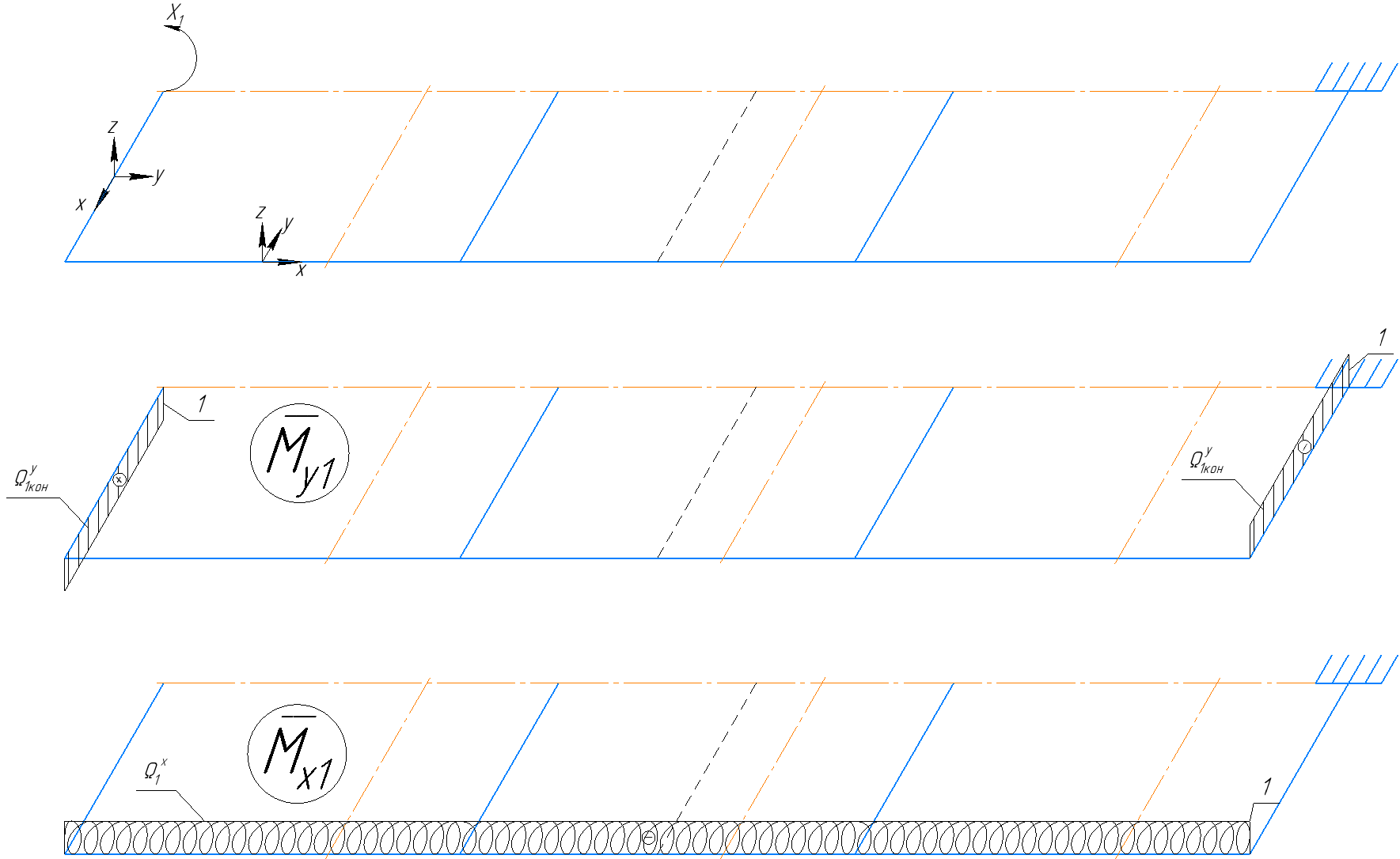 Рисунок 10 – Единичные эпюры от действия момента X1 2) Воздействие X2. 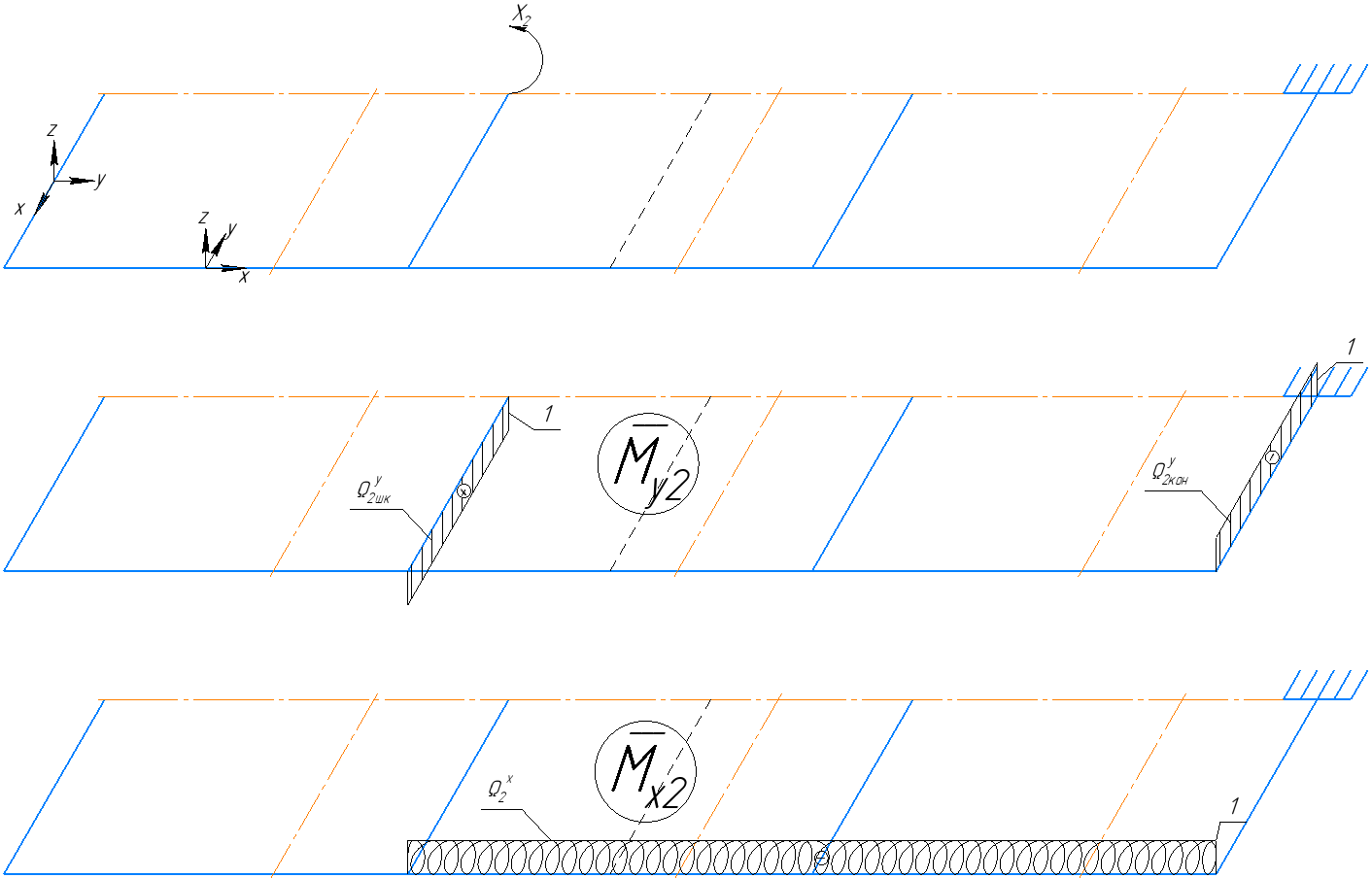 Рисунок 11 – Единичные эпюры от действия момента X2 3) Воздействие X3. 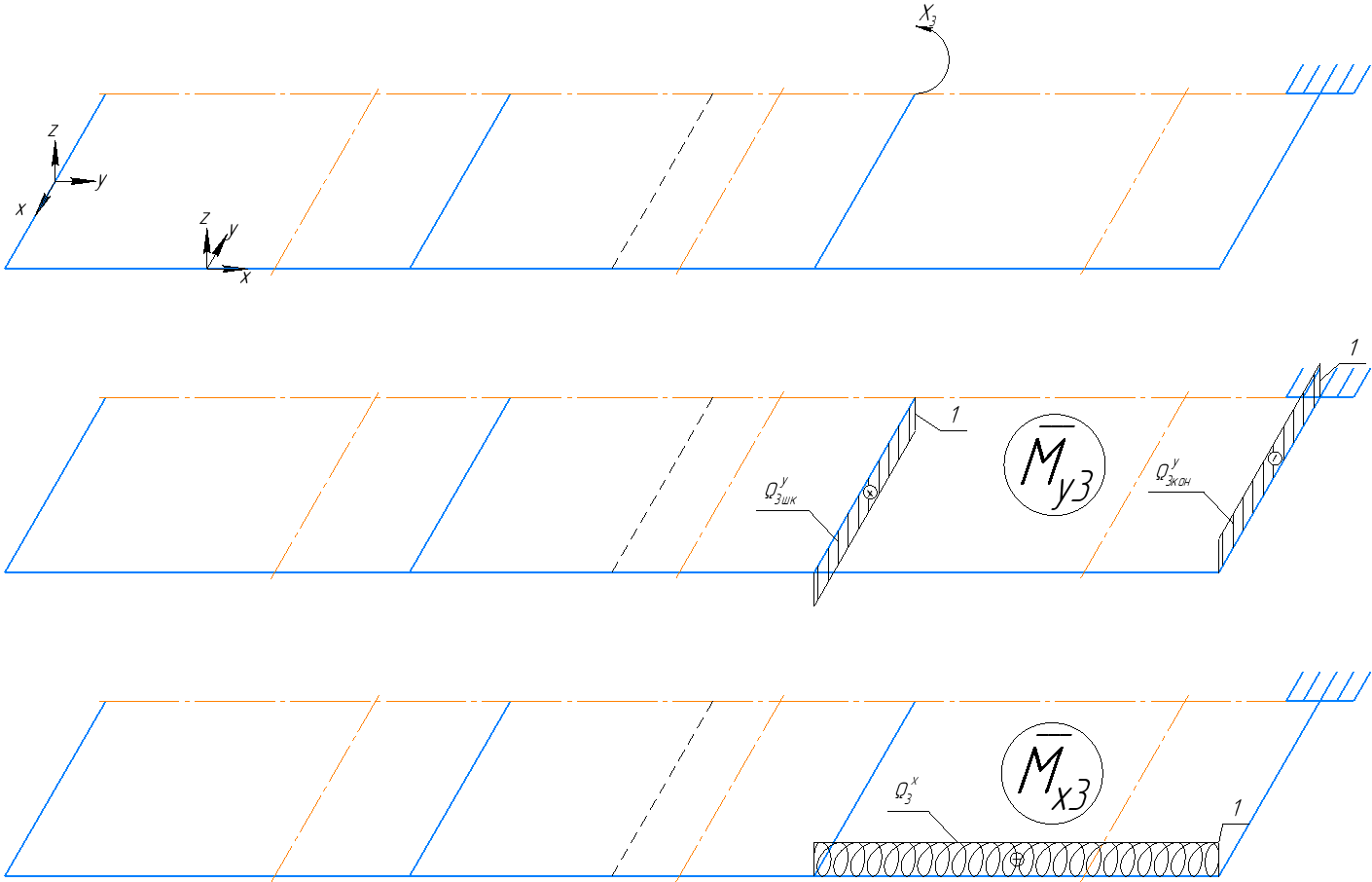 Рисунок 12 – Единичные эпюры от действия момента X3 4.5 Построение грузовых эпюр изгибающих и крутящих моментовПостроим эпюры изгибающих и крутящих моментов от внешних воздействий в основной системе. Определим моменты: 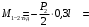 - -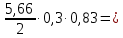 -0,7 кН∙м -0,7 кН∙м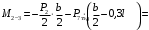 - -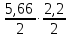 -7,97∙( -7,97∙(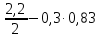 )= )==-3,68 кН∙м 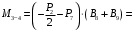 ( (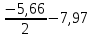 )∙(0,4+0,2)=-6,48 кН∙м )∙(0,4+0,2)=-6,48 кН∙м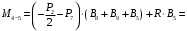 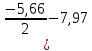 )∙(0,4+0,2+1,41)= )∙(0,4+0,2+1,41)=-21,71 кН∙м 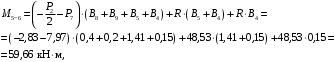 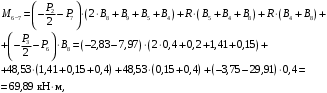 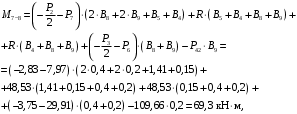 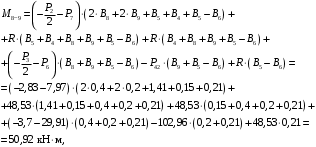 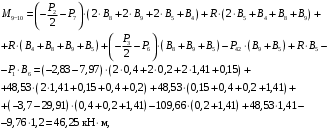   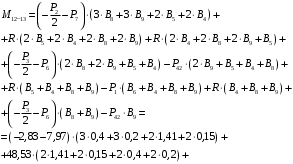  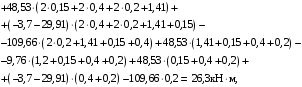  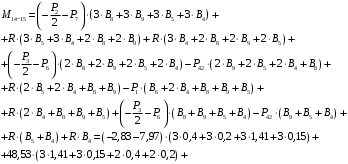 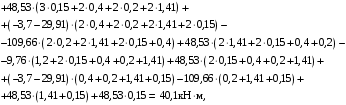 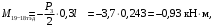 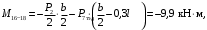 Так как к шкворневым балкам приложены одинаковые силы на одинаковом расстоянии, то M21‑20 = M19-18, M20-11 = M18-6. Отдельно построим эпюру изгибающих моментов на шкворневой балке. Разобьем это построение на 4 этапа. Сначала построим эпюру изгибающих моментов от действия силы 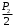 и и 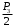 , потом от P6 и P7, затем от R, P1, P41,P42, P5, и в конце сложим 3 эпюры и получим результирующую. , потом от P6 и P7, затем от R, P1, P41,P42, P5, и в конце сложим 3 эпюры и получим результирующую.1) От действия сил 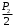 и и 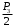 . .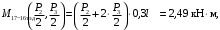 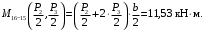 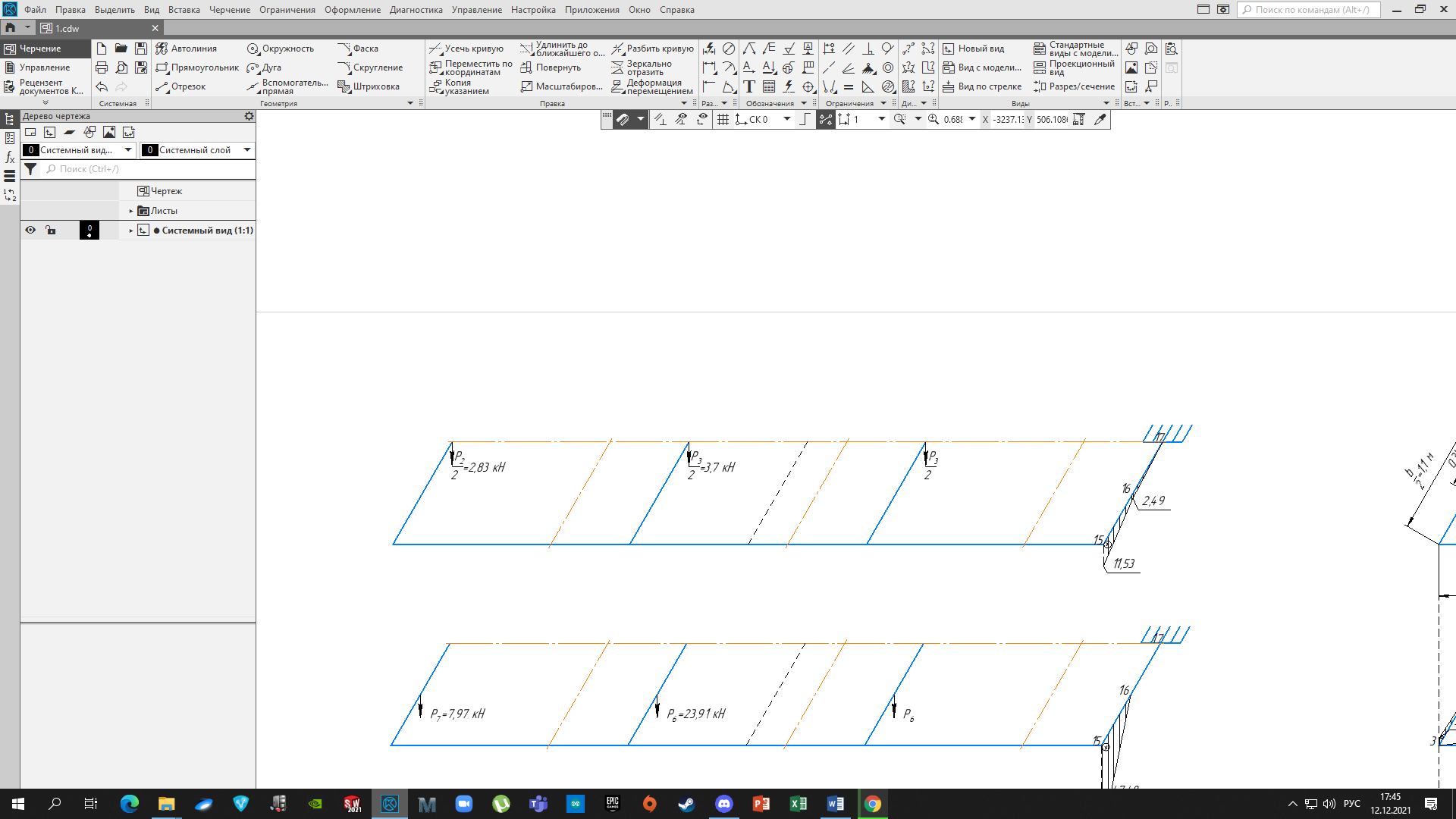 Рисунок 13 – Эпюра изгибающего момента шкворневой балки от действия сил 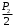 и и 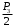 2) От действия сил P6 и P7. 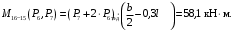 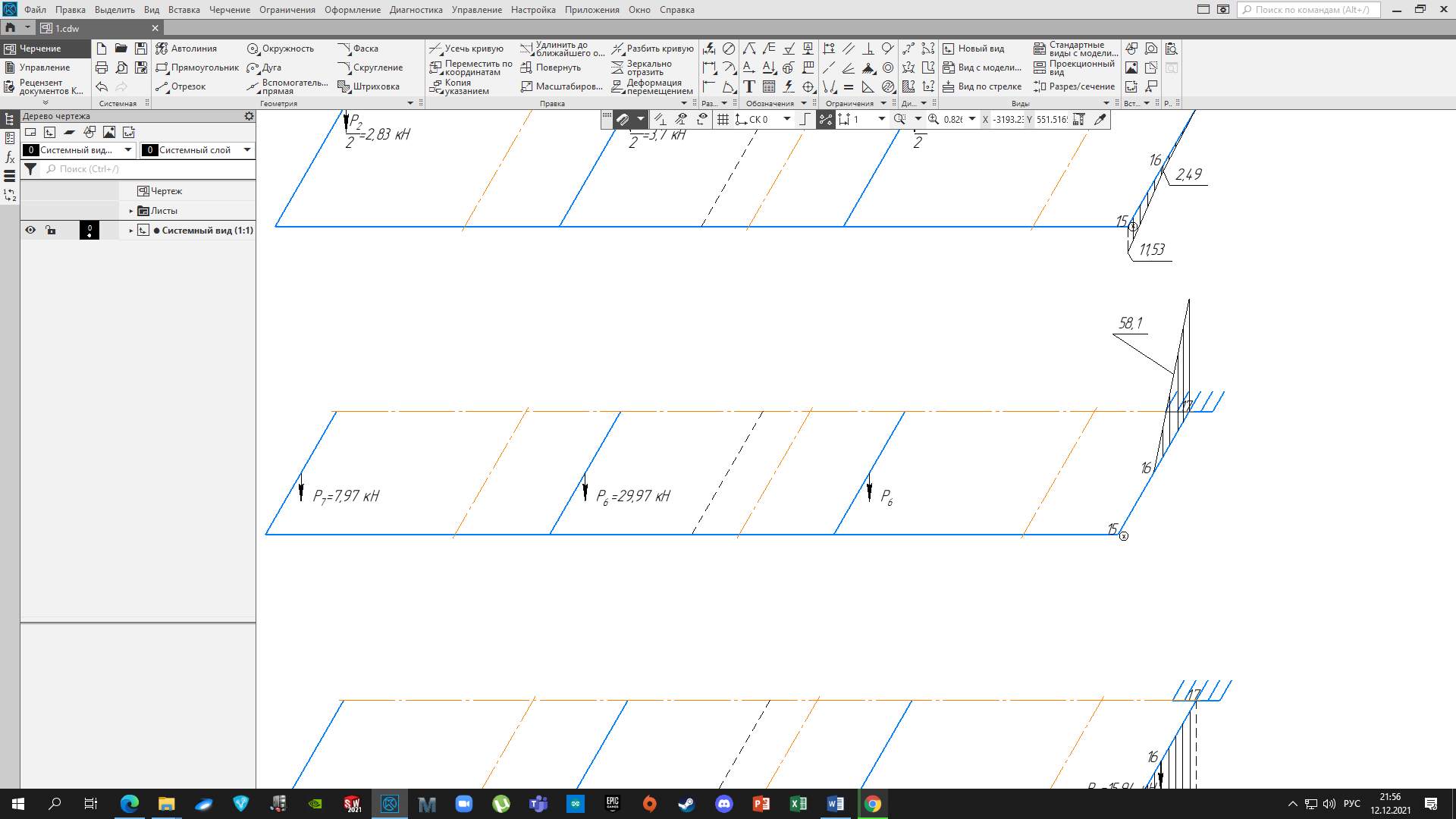 Рисунок 14 – Эпюра изгибающего момента шкворневой балки от действия сил P6 и P7 3) От действия сил R, P1, P41,P42, P5. 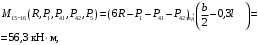 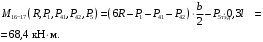 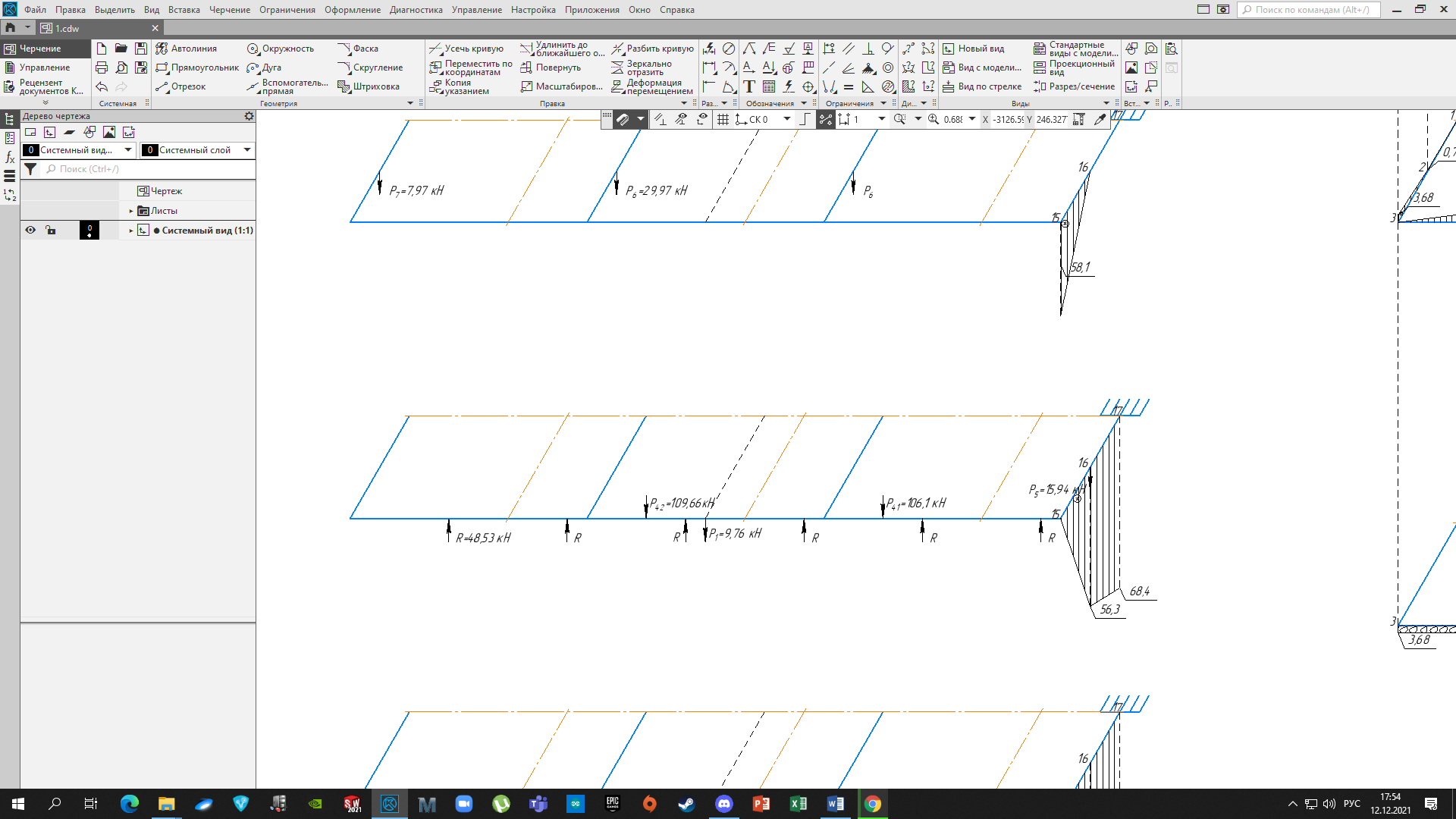 Рисунок 15 – Эпюра изгибающего момента шкворневой балки от действия сил R, P1, P41,P42, P5 4) Результирующая эпюра. 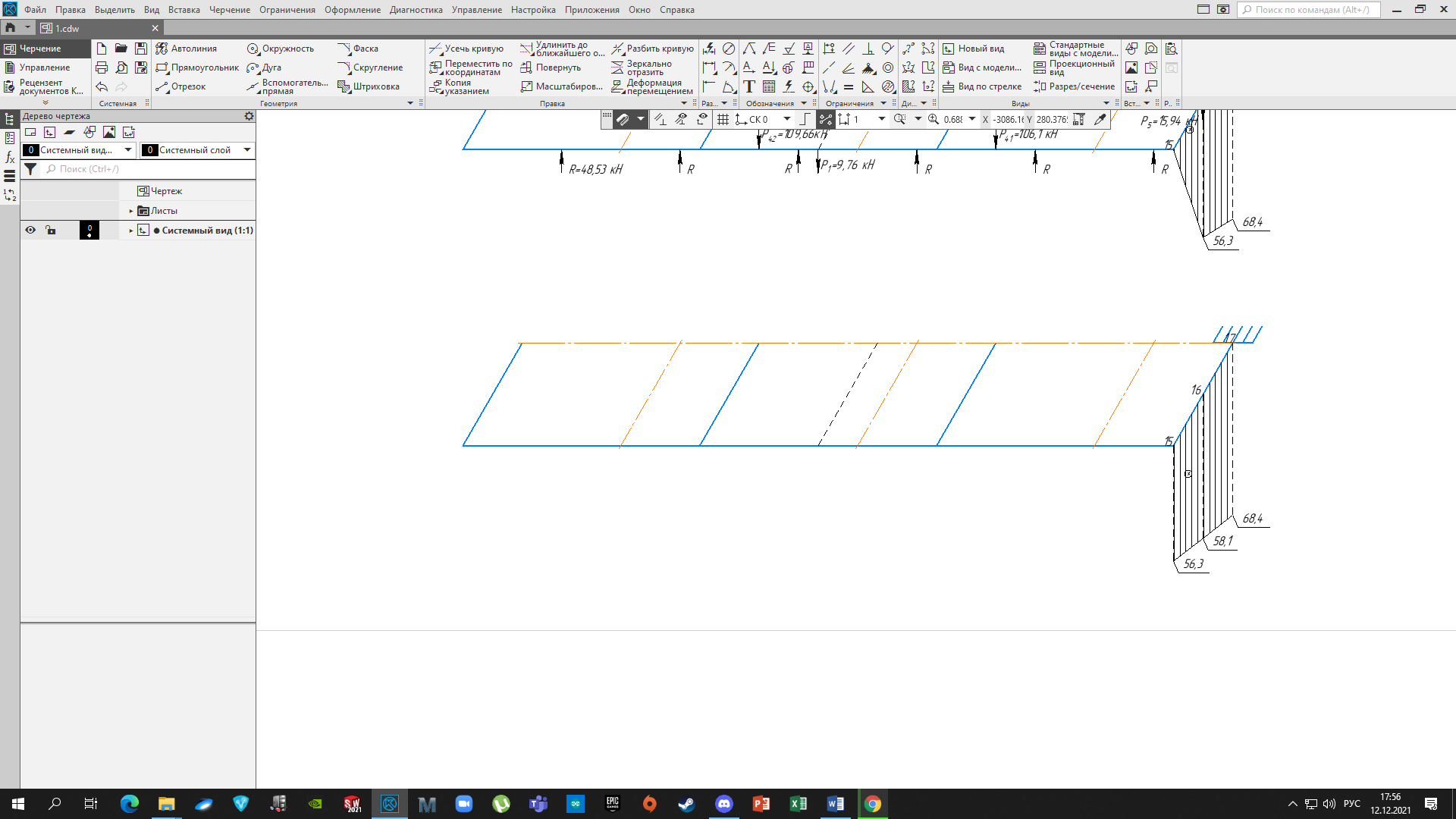 Рисунок 16 – Результирующая эпюра изгибающего момента шкворневой балки  Рисунок 17 – Грузовые эпюры изгибающих и крутящих моментов |
