Омпс. ОМПС лаба на сдачу. Лабораторная работа по дисциплине основы механики подвижного состава
 Скачать 3.08 Mb. Скачать 3.08 Mb.
|
4.6 Расчет коэффициентов и свободных членов системы уравнений метода силТак как в расчёте рамы тележки на прочность учитываются только деформации изгиба (относительно оси y) и кручения (относительно оси x), то выражения для вычисления коэффициентов и свободных членов канонических уравнений примут вид: 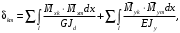 (14) (14)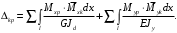 (15) (15)В нашем случае эпюры от единичных сил и внешней нагрузки являются линейными функциями координаты x. Поэтому для расчета δkm и Δkp используют способ Верещагина: 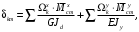 (16) (16)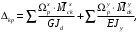 (17) (17)где 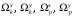 – площади эпюр соответственно крутящих и изгибающих моментов от действия единичной силы Xk= 1 и от заданной нагрузки; – площади эпюр соответственно крутящих и изгибающих моментов от действия единичной силы Xk= 1 и от заданной нагрузки;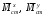 – ординаты единичных эпюр крутящих и изгибающих моментов от Xm = 1 под центром тяжести соответствующих единичных эпюр от Xk= 1; – ординаты единичных эпюр крутящих и изгибающих моментов от Xm = 1 под центром тяжести соответствующих единичных эпюр от Xk= 1;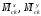 – ординаты единичных эпюр крутящих и изгибающих моментов от Xk = 1 под центром тяжести соответствующих грузовых эпюр. – ординаты единичных эпюр крутящих и изгибающих моментов от Xk = 1 под центром тяжести соответствующих грузовых эпюр.Рассчитаем площади единичных эпюр: 1) От X1 = 1: 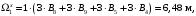 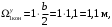 2) От X2 = 1: 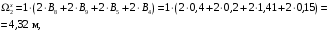 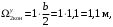 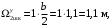 3) От X3 = 1: 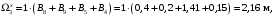 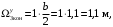 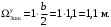 Ординаты единичных эпюр крутящих и изгибающих моментов в нашем случае равны 1 вне зависимости от расположения центра тяжести второй перемножаемой эпюры: 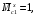 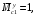 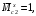 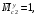 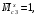 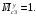 Рассчитаем площади грузовых эпюр изгибающих и крутящих моментов в пределах участков 1-3, 3-6, 19-6, 6-11, 21-11, 11-15, 15-17: 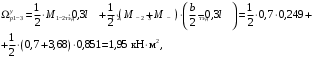 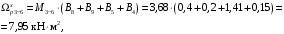 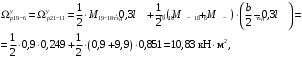 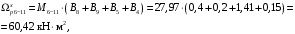 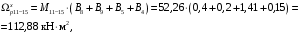 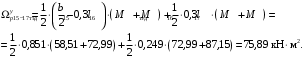 Упругие постоянные для стали: E = 2·108 кН/м2, G = 8·107 кН/м2. Канонические уравнения метода сил для определения X1,X2 и X3: 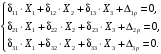 (18) (18)Рассчитаем коэффициенты δkm и Δkp по выражениям (16-17): 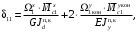 (19) (19)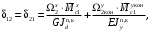 (20) (20)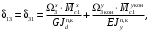 (21) (21)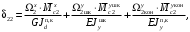 (22) (22)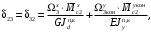 (23) (23)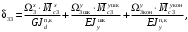 (24) (24)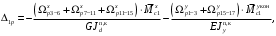 (25) (25)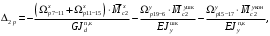 (26) (26)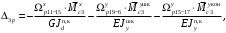 (27) (27)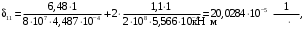 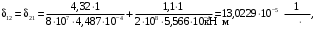 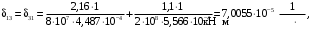 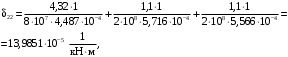 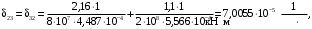 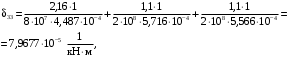 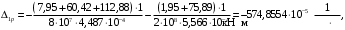 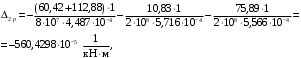  Таким образом, система канонических уравнений примет вид: 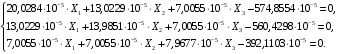 Проверим правильность найденных коэффициентов δkm и Δkp, для этого воспользуемся универсальной проверкой: если сумма всех коэффициентов системы канонических уравнений равна произведению суммарной единичной эпюры (рисунок 18) на себя, то коэффициенты вычислены верно: 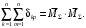 (28) (28)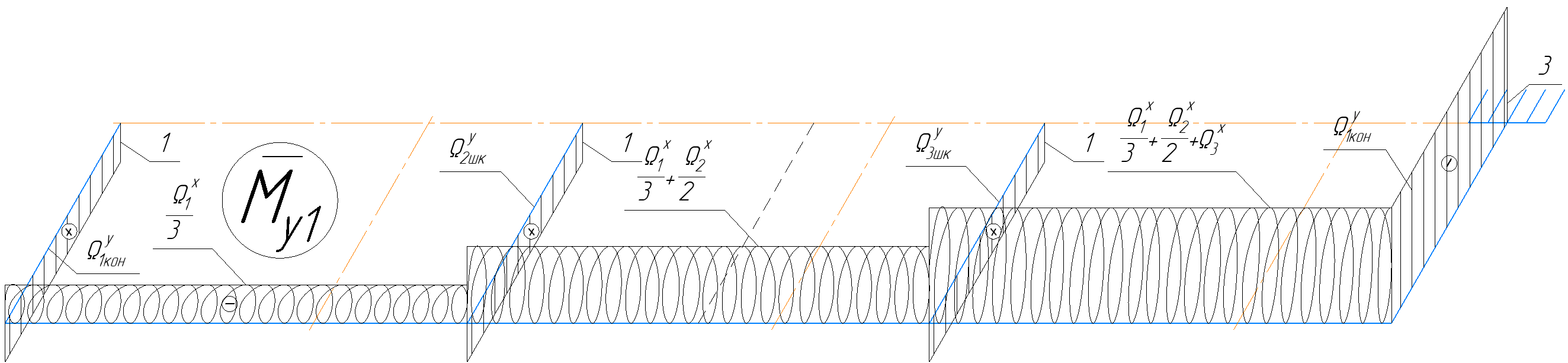 Рисунок 18 – Суммарная единичная эпюра 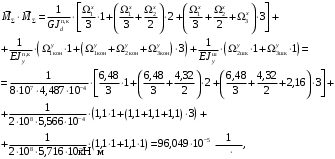 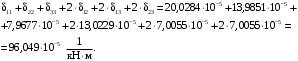 4.7 Решение системы уравнений методом сил. Построение суммарных эпюр изгибающих и крутящих моментовНайдём неизвестные X1 и X2, решив систему канонических уравнений: 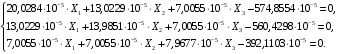 X1 = 5,22 кН·м, X2 = 22,98 кН·м, X3 = 24,42 кН·м. Ординаты суммарных эпюр изгибающих и крутящих моментов определим по выражениям: 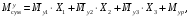 (29) (29)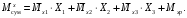 (30) (30)Построим эпюры от X1, X2 и X3, умножив единичные эпюры на X1, X2 и X3. 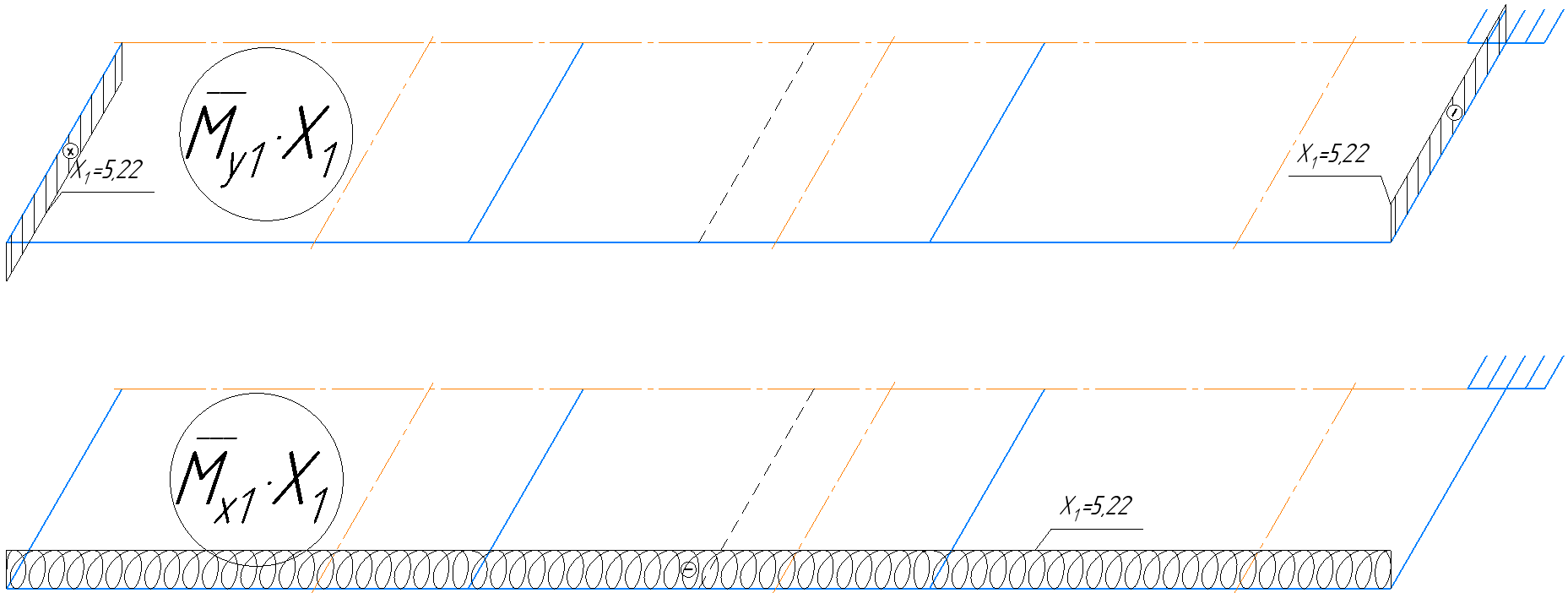 Рисунок 19 – Исправленные единичные эпюры от действия момента X1 = 5,22 кН·м 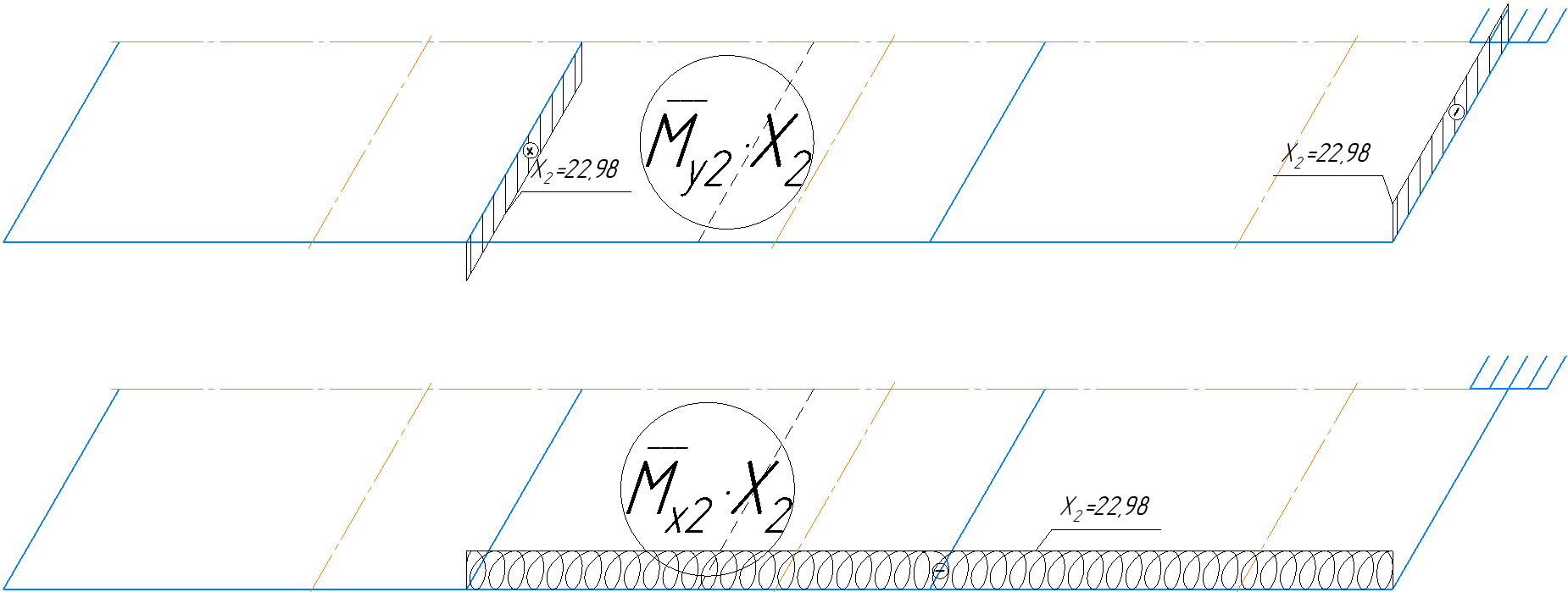 Рисунок 20 – Исправленные единичные эпюры от действия момента X2 = 22,98 кН·м 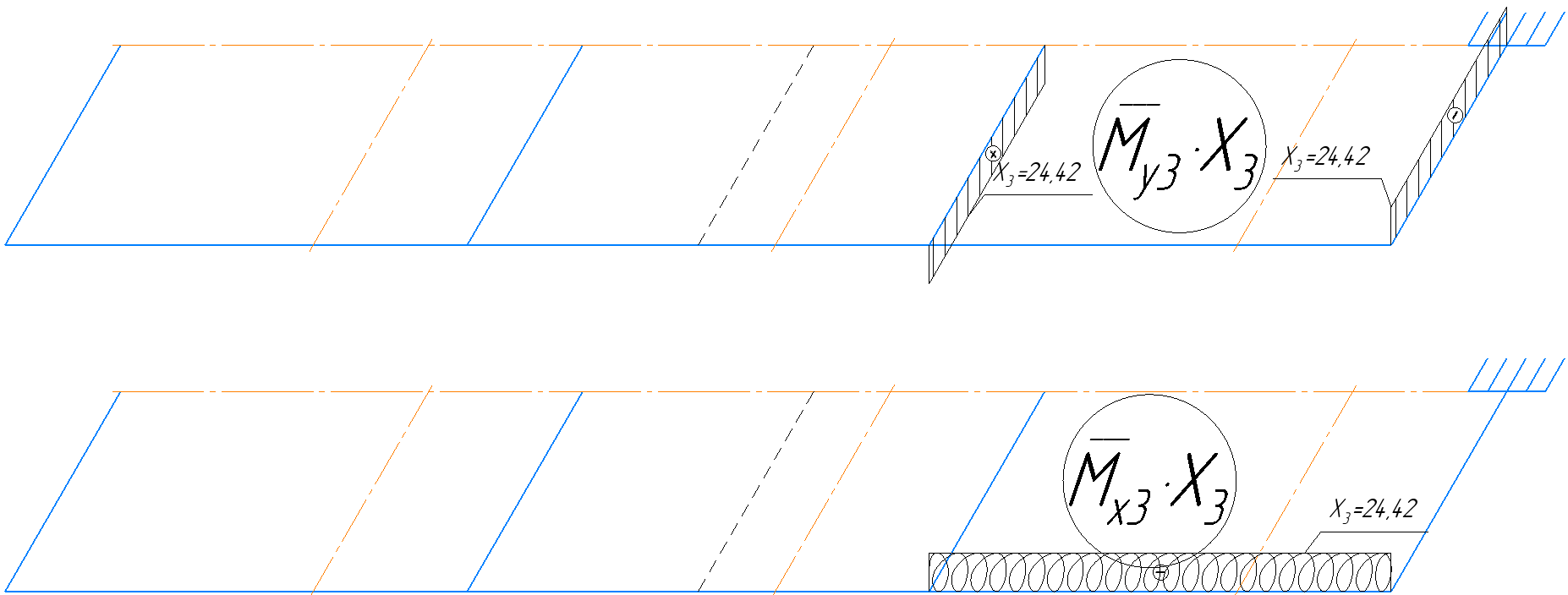 Рисунок 21 – Исправленные единичные эпюры от действия момента X3 = 24,42 кН·м Построим суммарные эпюры изгибающих и крутящих моментов, воспользовавшись выражениями (29) и (30). 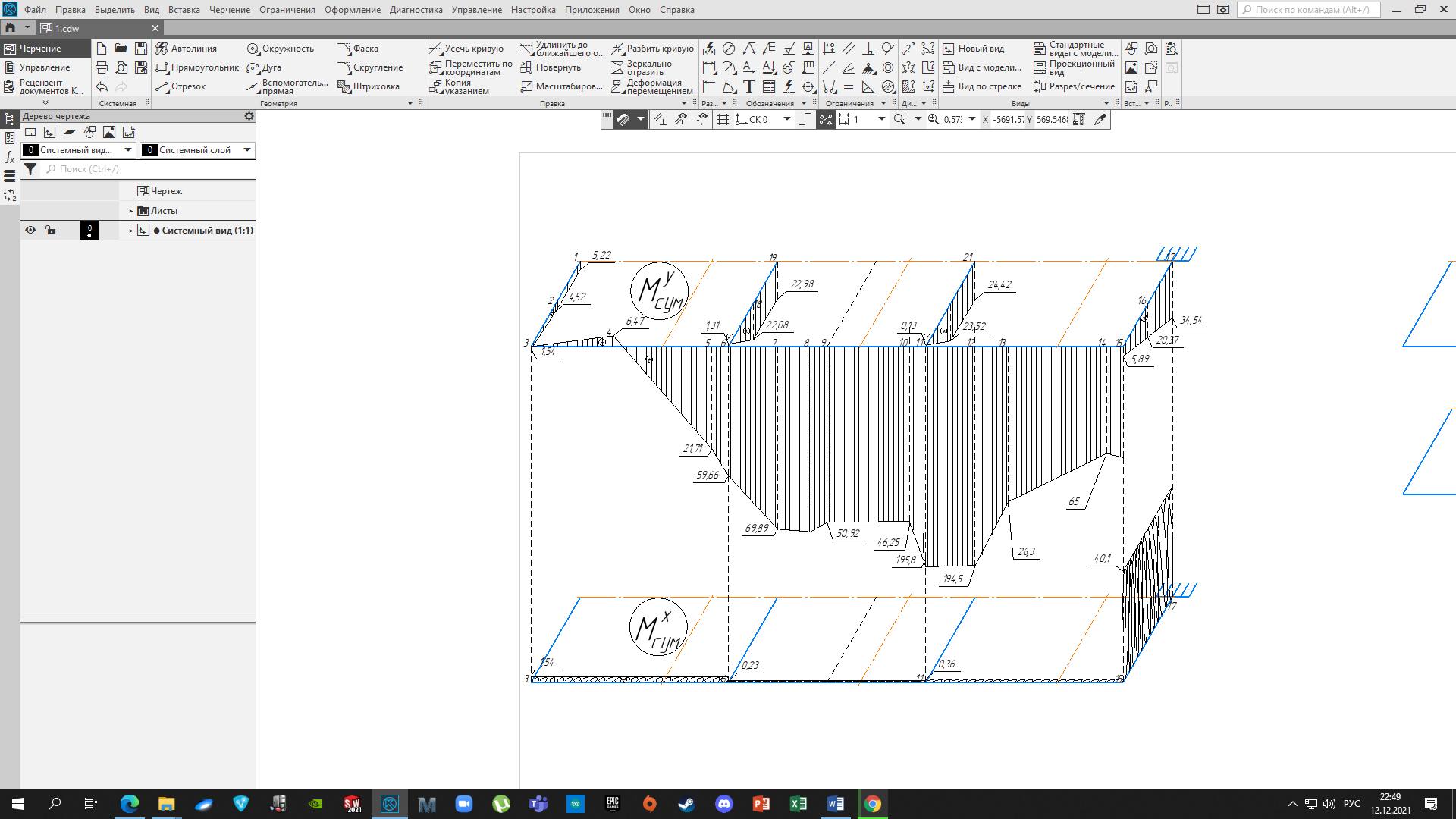 Рисунок 22 – Суммарные эпюры изгибающих и крутящих моментов 5 Анализ суммарных эпюр изгибающих и крутящих моментов. Определение опасных сеченийПосле построения суммарных эпюр изгибающих и крутящих моментов определим напряжения в тех точках балки, где внутренние силовые факторы значительны. Анализ суммарных эпюр на рисунке 22 показывает, что в нашем случае таких точек две – точка 12 и точка 21, которые находятся на продольной и концевой балках. В точке 12 действует нормальное напряжение σ, вызванное действием изгибающего момента 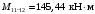 и касательное напряжение τ, обусловленное действием крутящего момента и касательное напряжение τ, обусловленное действием крутящего момента 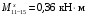 . . В точке 15 действует нормальное напряжение σ, вызванное действием изгибающего момента 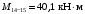 и касательное напряжение τ, обусловленное действием крутящего момента и касательное напряжение τ, обусловленное действием крутящего момента 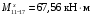 . . В точке 17 действует нормальное напряжение σ, вызванное действием изгибающего момента 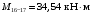 и касательное напряжение τ, обусловленное действием крутящего момента и касательное напряжение τ, обусловленное действием крутящего момента 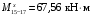 . . 6 Расчет нормальных, касательных и эквивалентных напряжений в опасных сечениях. Сравнение с допускаемыми значениямиНормальные напряжения определяют по формуле: 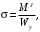 (31) (31)где Wy – момент сопротивления сечения при изгибе, м3. Для коробчатого сечения: 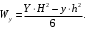 (32) (32)Касательные напряжения определяют по формуле: 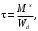 (33) (33)где Wd – момент сопротивления сечения при кручении, м3. Для коробчатого сечения: 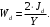 (34) (34)Для оценки прочности вычисляют эквивалентные напряжения на основе четвертой теории прочности: 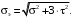 (35) (35)Полученные значения σэ не должны превышать допускаемые значения [σ], которые для двухосных тележек пассажирских электровозов равны [σ] = 150 МПа (сталь 52D в соответствии с EN 10327). Для рамы электровоза определим по формулам (31) и (33) значения Wy и Wd для продольных и концевых балок: 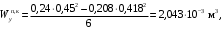 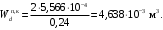 Рассчитаем нормальные, касательные и эквивалентные напряжения в точке 12: 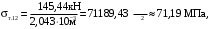 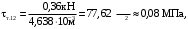 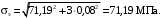 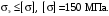 В точке 12 эквивалентное напряжение меньше допускаемого в 2,11 раза при коэффициенте запаса kσ = 1,7. Значит, продольная балка выдержит приложенную к ней нагрузку. В точке 17: 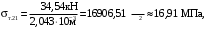 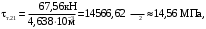 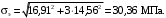 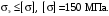 В точке 17 эквивалентное напряжение меньше допускаемого в 4,94 раза. Значит, шкворневая балка выдержит приложенную к ней нагрузку. ВыводыВ данной лабораторной работе была рассчитана на прочность тележка пассажирского электровоза с осевой формулой 30-30. В ходе данной лабораторной работы были рассчитаны размеры рамы тележки электровоза, рассчитана масса кузова и тележки, составлена весовая ведомость, разработана схема нагружения рамы тележки и рассчитаны действующие на нее вертикальные силы, рассчитана рамы тележки на прочность методом сил при действии вертикальной статической нагрузки, произведен анализ суммарных эпюр изгибающих и крутящих моментов, определены опасные сечения, произведен расчет нормальных, касательных и эквивалентных напряжений в опасных сечениях и сравнение с допускаемыми значениями. Их сравнение с допускаемыми напряжениями показало, что рама тележки электровоза ЧС4 с выбранными геометрическими размерами выдержит приложенную к ней нагрузку и будет иметь необходимый запас прочности. |
