ДИФРАКЦИЯ ЭЛЕКТРОНОВ. Кайль А.Ю Эл21с лабораторная1. Лабораторная работа по физике 13. Дифракция электронов рабо ту вы п о лнил ст г р. Эл21с кайль А. Ю рабо ту
 Скачать 74.73 Kb. Скачать 74.73 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Государственное бюджетное образовательное учреждение высшего образования «Башкирский государственный университет» Нефтекамский филиал Экономико – математический факультет Кафедра «Технических дисциплин» ЛАБОРАТОРНАЯ РАБОТА ПО ФИЗИКЕ №13. ДИФРАКЦИЯ ЭЛЕКТРОНОВ Работу выполнил: ст. гр.Эл21С Кайль А.Ю Работу принял: Кожевникова И.А., доц., канд. технич. наук Нефтекамск - 2022 ЛАБОРАТОРНАЯ РАБОТА №13. ДИФРАКЦИЯ ЭЛЕКТРОНОВ ЦЕЛЬ РАБОТЫ В данной работе с использованием компьютерной модели; исследуются процессы, возникающие при взаимодействии пучка электронов с непрозрачным для электронов экраном, имеющим узкую прямоугольную щель. Определяются некоторые характеристики, связанные с их движением. КРАТКАЯ ТЕОРИЯ Для описания движения многих материальных объектов достаточно единственной модели. Например, автомобиль, самолет, камень и другие «крупные» объекты можно описывать, используя только модель «материаль- ная точка» или «система материальных точек», которую можно называть корпускулярной. С другой стороны, электромагнитное излучение (ЭМИ) в классической физике рассматривают как волну (электромагнитную). Тем не менее, в некоторых ситуациях (условиях) такой классический подход не работает. Например, рассматривая процессы, происходящие в фотоэлементе, мы должны электромагнитное излучение сначала моделиро- вать, как волну (световую), распространяющуюся от источника до фотокато- да (волновая модель), а потом, как поток фотонов (корпускулярная модель), каждый из которых взаимодействует с одним электроном. Аналогичная ситуация возникает, в частности, при исследовании про- цессов, происходящих с участием микрочастиц. Квантовая физика имеет дело с двойственностью описания любых мате- риальных объектов . Это описание выглядит как совокуп- ность двух моделей - волновой и корпускулярной. Причем в одних усло- виях надо применять корпускулярную модель к данному объекту, а в других условиях к тому же объекту надо применять волновую модель. В начале про- шлого века эту проблему назвали «дуализм волна-частица». Волновая часть квантового описания объекта имеет много общего с вол- новой моделью, которую мы применяли в электромагнетизме (оптике), когда рассматривали движение электромагнитного излучения (поля). Простейшей волной является гармоническая волна, основными характе- ристиками которой являются амплитуда, частота и скорость распростране- ния. Корпускулярная часть квантового описания объекта выглядит как части- ца, имеющая массу, положение, траекторию и другие характеристики движе- ния. При исследовании взаимодействия пучка электронов с отверстием в не- прозрачном для них экране (в частности, с диафрагмой в электронно-лучевой трубке) в принципе можно наблюдать двойственный характер описания дви- жения электрона. Такой эксперимент возможно реализовать с помощью компьютерного моделирования реальной ситуации. Рассмотрим движение электрона в данном компьютерном эксперименте. При вылете из катода и движении до диафрагмы электрон можно моделиро- вать, как частицу, имеющую определенные кинематические характеристики: координату, скорость и ускорение. При прохождении через диафрагму мы должны моделировать электрон, как гармоническую волну, имеющую опре- деленную длину волны. При движении от диафрагмы до экрана электрон снова моделируем, как частицу, которая, попадая на экран, вызывает вспыш- ку зерна люминофора, покрывающего экран. Эту вспышку мы наблюдаем. Идеальный пучок электронов на языке корпускулярной модели есть со- вокупность параллельно движущихся частиц, имеющих одну и ту же ско- рость. Взаимодействие с непрозрачной для электронов диафрагмой, имею- щей отверстие, анализируем, моделируя электроны, как волны, имеющие длину волны определяемую соотношением де Бройля: …………………………………. ИЗМЕРЕНИЯ 1. Установите для модели «вид экрана «Одна щель»» (кнопки слева внизу). 2. Щелкните кнопку «Сброс» (нижняя часть кнопки управления) для очистки поля модели. 3. Установите ширину щели по табл. 1 в соответствии с номером вашей бригады. Таблица 1 Значения ширины щели Δх 10-10 м для разных бригад 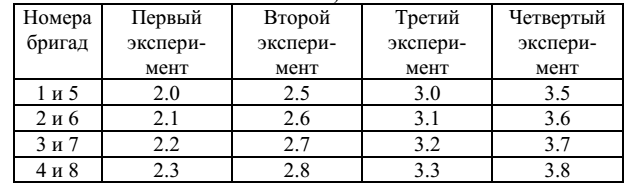 4. Щелкните мышью по кнопке «Пуск». Снова щелкните мышью по этой кнопке (которая теперь называется «Пауза»), когда количество вспышек электронов в зоне ПЕРВОГО МАКСИМУМА дифракционной картины составит 5 –7. 5. Прикладывая горизонтально лист бумаги или линейку, соедините положение каждого электрона первого максимума с вертикальной шкалой на экране и определите координаты xi всех электронов этой группы, начиная с верхнего (i – номер электрона по порядку). Запишите результаты в соответствующую строку табл. 2. Таблица 2 Координаты электронов первого дифракционного максимума. Ширина щели Δх1 = __2*___10-10 м (первый эксперимент)
6. Закончив измерение и запись координат всех электронов первого максимума, щелкните кнопку «Выбор» и установите следующее значение ширины щели по табл. 1. 7. Повторите измерения по пп. 5 - 8, записывая результаты в табл. 3 - 5. Таблица 3 Координаты электронов первого дифракционного максимума. Ширина щели Δх2 = __2.5*___10-10 м (второй эксперимент)
Таблица 4 Координаты электронов первого дифракционного максимума. Ширина щели Δх3 = __3*___10-10 м (третий эксперимент)
Таблица 5 Координаты электронов первого дифракционного максимума. Ширина щели Δх4 = _3.7____10-10 м (четвертый эксперимент)
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА 1. Вычислите средние значения координат электронов первого дифракционного максимума при каждом значении ширины щели 2. Постройте график зависимости среднего значения координаты первого максимума от обратной ширине щели График зависимости 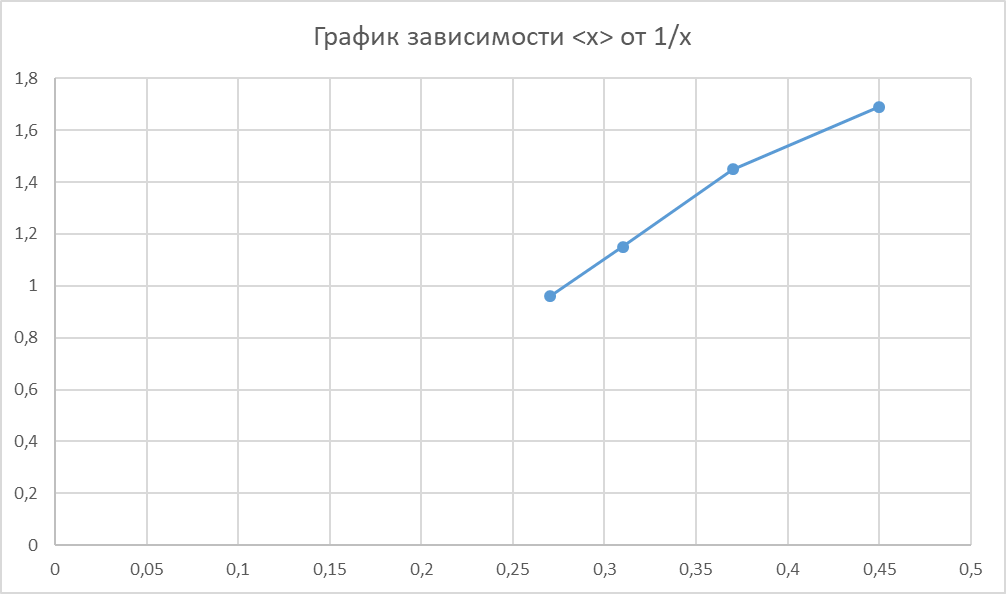 3. По графику или обработав точки методом наименьших квадратов, определите наклон прямой и, подставив его в формулу (8), 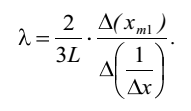 вычислите длину волны электрона. вычислите длину волны электрона.Например, λ= 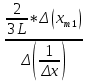 ≈ 2.4* ≈ 2.4*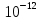 м ≈2.428* м ≈2.428*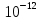 м. м.4. Сделайте вывод по полученному графику зависимости 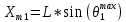 = =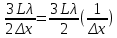 . .Получились, с учетом погрешности, примерно похожими. 5. Сделайте вывод по полученному значению λ, сравнивая его с числом, приведенным на экране компьютера. Данное значение, с учетом погрешности, примерно равно табличному значению длины волны электрона. ВЫВОД: В данной работе мы с использованием компьютерной модели; исследовали процессы, возникающие при взаимодействии пучка электронов с непрозрачным для электронов экраном, имеющим узкую прямоугольную щель. Определили некоторые характеристики, связанные с их движением. ВОПРОСЫ и ЗАДАНИЯ ДЛЯ САМОПОДГОТОВКИ Сформулируйте модель, описывающую состояние движения микрообъекта, применяемую в квантовой физике? Модель, описывающая состояние движения микрообъекта в квантовой физике имеет двойственный характер и выглядит, как совокупность двух моделей - волновой и корпускулярной. Какая классическая модель ЭМИ применяется в электромагнетизме? Электромагнитное излучение (ЭМИ) в классической физике рассматривают, как волну (электромагнитную). Назовите примеры классических моделей объектов, применяемых в механике. Объекты механики можно описывать, используя классические модели «материальная точка», «система материальных точек», «абсолютно твердое тело» и др. Какую модель надо применять при исследовании движения самолета из Москвы в Сочи? При исследовании движения самолета из Москвы в Сочи следует применять модель «материальная точка». Каково устройство электронно-лучевой трубки? Электронно-лучевая трубка имеет вакуумированную стеклянную колбу, в которую установлены катод, эмитирующий электроны, управляющие электроды и люминисцентный экран. Какова волновая модель электрона, если это частица, движущаяся с постоянной скоростью? Волновой моделью электрона, движущегося с постоянной скоростью, является гармоническая волна. Напишите формулу для длины волны де Бройля. Длина волны де Бройля для частицы массы m, движущейся со скоростью V, λ = h/(mV). Что такое явление дифракции? Дифракцией называется огибание волной области неоднородности, возникающее, например, при наличии непрозрачного экрана, имеющего щель или границу. При этом нарушаются законы геометрической оптики, в частности, волна проникает в область геометрической тени, и возникают интерференционные явления. Как выглядит волновая функция свободно движущейся частицы? Волновая функция свободно движущейся частицы имеет вид гармонической функции, зависящей от координаты и времени psi(t) = psi0 sin(omega t - kx) Почему у электрона, проходящего через щель, появляется вертикальная (в данной компьютерной установке) составляющая импульса? При движении через щель электроны могут изменить направление своего движения, приобретя дополнительный импульс в вертикальном направлении, поскольку внутри щели у них имеется неопределенность вертикальной координаты, равная ширине щели. Каков физический смысл (волновой функции) приписываемой электрону?? Физический смысл волны (волновой функции) электрона: квадрат модуля волновой функции определяет плотность вероятности нахождения электрона вблизи данной точки. Напишите соотношение для синуса угла минимума при дифракции на прямоугольной щели. Для угла n-го минимума theta nmin при дифракции на прямоугольной щели: sin(theta nmin) = n(lambda/∆x) Напишите соотношение для синуса угла максимума при дифракции на прямоугольной щели. Для угла n-го максимума при дифракции на прямоугольной щели sin(theta nmax) = (n+1/2)(lambda/∆x) . Чему прямо пропорциональна координата xm1 первого максимума дифракционной картины на экране? Смещение первого максимума по вертикальной оси Xm1 пропорционально расстоянию L от диафрагмы до экрана и тангенсу угла theta lmax , под которым наблюдается первый максимум: Xm1 = L·tg(theta 1max) . Какой формы график вы ожидаете получить при построении зависимости График зависимости среднего значения координаты первого максимума от обратной ширины щели через начало координат. Как вы определите длину волны де Бройля для электрона в данной работе? Чтобы определить длину волны де Бройля электрона в данной работе надо по графику найти тангенс угла наклона прямой формулу: lambda = (2/3)·L·[∆Xm1/∆(1/∆x)] С чем вы будете сравнивать полученное числовое значение длины волны де Бройля для электрона? Рассчитанное числовое значение длины волны электрона lambda надо сравнить со значением, приведенным на экране. Какие выводы вы предполагаете сделать после исследования вида полученного графика Вывод по данному графику | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
