лаб 15. Лаб раб 15. Лабораторные работы

• Название: Лабораторные работы
• Анкор: лаб 15
• Дата: 22.09.2022
• Размер: 0.6 Mb.
• Имя файла: Лаб раб 15.docx
• Тип: Документы; #690117
• страница: 13 из 26

Конгруэнтный генератор со случайными параметрами

^{Еще один способ комбинирования двух генераторов G}1^{, G}2 ^{заключается в том, что G}1 ^{изменяет параметры генератора G}2 ^{с течением времени. Проиллюстрируем это в случае, когда G}2 ^{– линейный конгруэнтный генератор:}

x_t a_tx_t1  b_t mod N,

t1, 2, ...

(10)

^{где x}0 ^{ A– некоторое стартовое значение, а}

 ^a


t
A_t ^ _b^ B,

t 1, 2, ...
– некоторая

 t

псевдослучайная последовательность векторов, равномерно распределенных в B.

^{Доказано, что если |B| = 3, то наибольшее приближение распределения {x}t^{} к} равномерному достигается, если множество параметров Bимеет следующий вид:

^ ³

B _^ ₀^,

³

^{ },

1

 ³^

 ₂_ .

<sup> 

   </sup>

Проверка качества сгенерированной последовательности

Для проверки гипотезы о том, что сгенерированная последовательность подчиняется равномерному распределению, можно использовать критерий согласия χ²-Пирсона.

Сначала отрезок, содержащий числа, которые могут быть смоделированы, разбивают на Kинтервалов (интервалы обычно выбирают равной длины) и считают, сколько ^{элементов последовательности, длина которой N, попадает в каждый интервал (}i^{). Пусть} M – максимально возможный элемент в последовательности длиной N, тогда если M < 10, то K = M, иначе K≈ 5∙lg N.

Затем вычисляют статистику критерия по формуле:

^ ²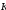

S^*  N _

i1

_i_{ Pi}

^N  _,

P_i

^{где P}i^{– теоретическая вероятность попадания в i-й интервал (для равномерного распределения P}i<sup>= 1 / K, если интервалы равной длины).

Если вычисленная статистика S* больше критического значения статистики S</sup>кр^при заданных степени свободы (r = K – 1) и уровне значимости (α = 0.05), то гипотеза отвергается, иначе нет оснований для отклонения проверяемой гипотезы.

^Sкр^{можно взять из статистической таблицы (например, по адресу} http://ami.nstu.ru/headrd/applied/xi_point.htm) или вычислить самостоятельно, используя какой-нибудь математический пакет. Например, в Maple 12 это можно сделать следующим образом:
with(Statistics):

alpha:=0.05; # Уровень значимости r:=9; # Степень свободы

S[kr]:=Quantile(ChiSquare(r),1-alpha); # Критическое значение статистики