лаб 15. Лаб раб 15. Лабораторные работы
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
Последовательности, порождаемые линейными регистрами сдвига с обратной связьюЛинейным регистром сдвига с обратной связью (Linear Feedback Shift Register, сокращенно LFSR) называется логическое устройство, схема которого изображена на рис. 1. 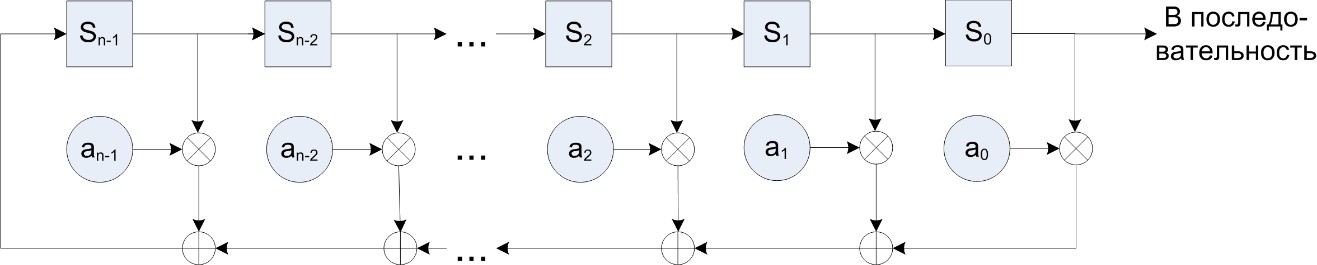 Рисунок1 – Блок-схема LFSR LFSR состоит из nячеек памяти, двоичные состояния которых в момент времени t = 0, 1, … характеризуются значениями S0(t), S1(t), … , Sn–1(t) A = {0, 1}. Выходы ячеек памяти связаны не только последовательно друг с другом, но и с сумматорами в соответствии с коэффициентами передачи a0, a1, … , an–1 A: если ai = 1, то значение Si(t) i-ой ячейки передается на один из входов i-го сумматора; если же ai = 0, то такая передача отсутствует. Обычно коэффициенты передачи задаются с помощью полинома: fx an xn a n1 xn1 a n2 xn2 ... a x2 ax a 1 2 0 Состояние LFSR в текущий момент времени tзадается двоичным n-вектор-столбцом S(t) = (Sn–1(t), … , S0(t))'. Содержание ячеек LFSR с течением времени изменяется следующим образом, определяя тем самым динамику состояний LFSR: Si1 (t), S(t1) n1 еслиi 0, n 2, (8) iajSj(t), j0 еслиi n1 Текущие значения нулевой ячейки регистра используются в качестве элементов порождаемой LFSR двоичной псевдослучайной последовательности sy= S0(t) (см. рис. 1). Модель (8) является частным случаем модели (7) линейной рекурренты над полем GF(2n ) , поэтому коэффициенты {ai} выбираются согласно методике, приведенной в предыдущем пункте. Т.е. многочлен, по которому строится LFSR, должен быть примитивным по модулю 2. Степень многочлена является длиной сдвигового регистра. Примитивный(базовый)многочленстепениnпомодулю2–это неприводимый многочлен, который является делителем x2n 1 1, но не является делителем xd1 для всех d, являющихся делителями 2n1. Неприводимый многочлен степени n нельзя |
