Лабораторное занятие 1
 Скачать 27.72 Kb.
|
|
ЛАБОРАТОРНОЕ ЗАНЯТИЕ № 1 Анализ определения и задания потоков вызовов. Основные свойства потоков вызовов. Основные характеристики потоков вызовов. Цель работы: Изучить свойства и характеристики простейшего потока. Сравнить теоретические и модельные значения полученных характеристик. Подготовка к работе Изучить и освоить теоретический материал по свойствам и характеристикам простейшего потока вызовов. Задание к работе На алгоритмическом языке Паскаль разработать программу, с помощью которой необходимо получить последовательность tk моментов поступления вызовов в промежутке [T1 , T2 ]. Промежутки между моментами поступления вызовов zi = ti+1 – ti должны быть распределены по показательному закону c интенсивностью λ. Значения T1 , T2 и λ определить по варианту. Полученные данные свести в таблицу 2. Т а б л и ц а 2
Здесь rj - случайное число, равномерно распределенное в промежутке (0, 1); zj – промежуток между моментами поступления вызовов; tj - моменты поступления вызовов. 1.3.3 Провести статистическую обработку полученных результатов, для этого разделить заданный интервал на 24 равных промежутка длиной t =  , (мин).Для каждого промежутка определить x (t ) – количество вызовов, попавших в промежуток, длиной t и заполнить таблицу 3. Т а б л и ц а 3
Получить таблицу статистического распределения случайной величины Т а б л и ц а 4
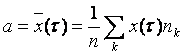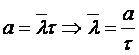n = å nk = 24 nk - количество интервалов, в которое попало к вызовов. 1.3.4 Определить модельное значение параметра потока  - мат. ожидание числа вызовов в к интервале.  .1.3.5 Для заданного ( l ) и модельного значения (  ), определить:а) вероятность отсутствия вызовов P0 ( t ) за промежуток t = T2 - T1 ; б) вероятность поступления одного вызова P1 ( t ) ; в) вероятность поступления четырёх вызовов P4 ( t ); г) вероятность поступления не менее пяти вызовов P³5 ( t )=1-( P0 + P1 + P2 + P3 + P4 ). Порядок выполнения работы 1 Получить задание и вариант работы у преподавателя. 2 Разработать алгоритм и программу. 3 Осуществить ввод программы и её отладку. 4 Получить результаты работы программы. 5 Статистическую обработку полученных данных провести в Excel. 6 Сделать выводы и анализ полученных результатов. 7 Подготовить отчет о выполненной работе, где представить алгоритм и листинг программы, результаты вычислений и анализ полученных данных. Материалы для подготовки к лабораторной работе Случайные потоки вызовов классифицируются в зависимости от наличия или отсутствия следующих трех свойств: стационарности, последействия и ординарности. Стационарность означает, что с течением времени вероятностные характеристики потока не меняются, иначе говоря, для стационарного потока вероятность поступления i вызовов за промежуток времени t зависит только от длины этого промежутка и не зависит от расположения его на оси времени. Ординарность означает невозможность группового поступления вызовов, то есть вероятность поступления двух и более вызовов за любой бесконечно малый промежуток есть величина бесконечно малая. В сетях связи потоки вызовов ординарны. Последействие означает зависимость вероятностных характеристик вызовов от предыдущих событий. К основным характеристикам потока вызовов следует отнести ведущую функцию потока, его параметр и интенсивность. Ведущая функция   случайного потока есть математическое ожидание числа вызовов в промежутке [0,t). Функция - неотрицательная, неубывающая.Под параметром потока λ(t) в момент времени t понимается предел отношения вероятности поступления не менее одного вызова в промежутке [t,t+Dt] к длине этого промежутка Dt при Dt → 0:
λ(t) = Согласно определению стационарного потока, вероятность поступления определённого числа вызовов за некоторый промежуток времени одна и та же, не зависит от месторасположения на оси времени этого промежутка. Следовательно, и плотность вероятности поступления вызовов стационарного потока, то есть его параметр λ(t) есть величина постоянная, не зависящая от момента t, то есть λ(t) = λ . Параметр потока μ(t) характеризует не поток вызовов, а поток вызывающих моментов, и эта характеристика относится не ко всему отрезку [0,t], а лишь к фиксированному моменту t. Интенсивность стационарного потока μ есть математическое ожидание числа вызовов, поступающих в единицу времени. Для ординарных потоков μ=λ=const. Стационарный, ординарный поток без последействия называется простейшим. Задается простейший поток семейством вероятностей  (t) поступления i вызовов в промежутке t .Вероятность (t) вычисляется по формуле (t)=  (2.1)где λ- параметр потока, постоянная величина, поскольку поток стационарный, λ=μ, поскольку поток ординарный. Формула (2.1) называется формулой Пуассона или распределением Пуассона. Простейший поток можно задать еще следующим способом: функцией распределения промежутка между соседними вызовами z F(t)=P(z>t)=1- (t)=1- . (2.3)Закон распределения (2.3) называется показательным, а λ его параметром. Рассмотрим свойства и характеристики простейшего потока. Математическое ожидание величины промежутка между соседними вызовами z , равна Mz=1/λ. Дисперсия данной величины равна 1/  , следовательно,среднеквадратическое отклонение σz= 1/λ, то есть имеет место равенство Mz = σz= 1/λ. Математическое ожидание числа вызовов i за промежуток времени t равно λt, дисперсия числа вызовов за промежуток t равна также λt, то есть Mi = Di = λt. Cовпадение этих величин используют на практике при проверке соответствия реального потока простейшему. 1.6 Варианты лабораторной работы Т а б л и ц а 5
Контрольные вопросы 1 По каким свойствам классифицируются случайные потоки ? 2 Дать определение свойствам случайных потоков (стационарность, ординарность, отсутствие последействия). 3 Дать определения числовым характеристикам случайных потоков (параметр потока  , интенсивность потока  , ведущая функция потока). |
