лекции. 3 Лекции НСХТ. Лекции по дисциплине Надежность сельскохозяйственной техники Тема 1. Введение. Цель и задачи курса. Цель Изучение теории надежности транспортной техники План

• Название: Лекции по дисциплине Надежность сельскохозяйственной техники Тема 1. Введение. Цель и задачи курса. Цель Изучение теории надежности транспортной техники План
• Анкор: лекции
• Дата: 18.05.2023
• Размер: 2.82 Mb.
• Имя файла: 3 Лекции НСХТ.doc
• Тип: Лекции; #1140950
• страница: 4 из 7

Тема 7,8. Основные понятия и термины надежности техники. Количественные характеристики надежности.

Цель: Изучение понятий теории надежности технологических машин.

План:

1. Системы и элементы расчета.

2. Количественные характеристики надежности.

3. Показатели долговечности.

4. Показатели ремонтопригодности и сохраняемости.

5. Комплексные показатели надежности.
7.1 Системы и элементы расчета.

Квалиметрия – научная область, объединяющая количественные методы оценки качества, используемые для обоснования решений, принимаемых при управлении качеством продукции и стандартизации.

Показатели качества продукции – это количественная характеристика одного или нескольких ее свойств, составляющих качество. Этот показатель рассматривают применительно к условиям создания, эксплуатации или потребления продукции. Различают следующие показатели качества продукции.

Единичный показатель – показатель, характеризующий только одно свойство продукции.

Комплексный показатель – показатель, характеризующий несколько свойств продукции.

Интегральный показатель – отношение суммарного полезного эффекта от эксплуатации или потребления продукции к суммарным затратам на ее создание и эксплуатацию или потребление.

Оценка надежности технических объектов также возможна с помощью показателя надежности.

Показатель надежности – количественная характеристика одного или нескольких свойств, составляющих надежность технического объекта, т.е. он количественно характеризует, в какой степени конкретному объекту присущи определенные свойства, обуславливающие его надежность.

Для определения числовых значений надежности могут быть использованы как точные (теоретические), так и приближенные (статистические) уравнения.

Многие показатели надежности – это параметры распределения случайных величин. Для их оценки основными величинами, участвующими в расчетах, приняты следующие случайные величины; наработка, число отказов и число объектов, находящихся в эксплуатации или на испытаниях.

В соответствии с ГОСТ для количественной оценки надежности применяют единичные и комплексные показатели надежности.

Единичный показатель – количественно характеризует только одно свойство надежности объекта, т.е. этот показатель к одному из свойств, составляющих надежность объекта(безотказность, долговечность, ремонтопригодность или сохраняемость).

Комплексный показатель – количественно характеризует одновременно два или несколько различных свойств технического объекта, т.е. он относится к нескольким различным свойствам, составляющих надежность технического объекта.
7.2.Количественные характеристики надежности.

Количественные показатели надежности могут быть получены на основании анализа эксплуатации или данных стендовых испытаний с последующим пересчетом применительно к условиям эксплуатации, путем измерений с последующим сравнением с предельными характеристиками материалов и деталей, полученных расчетным путем. Схема определения показателей надежности приведена на рисунке 11.

Количественные характеристики надежности носят вероятностный характер. Оценивать и анализировать их следует в зависимости от закона распределения, которому подчиняются исследуемые параметры.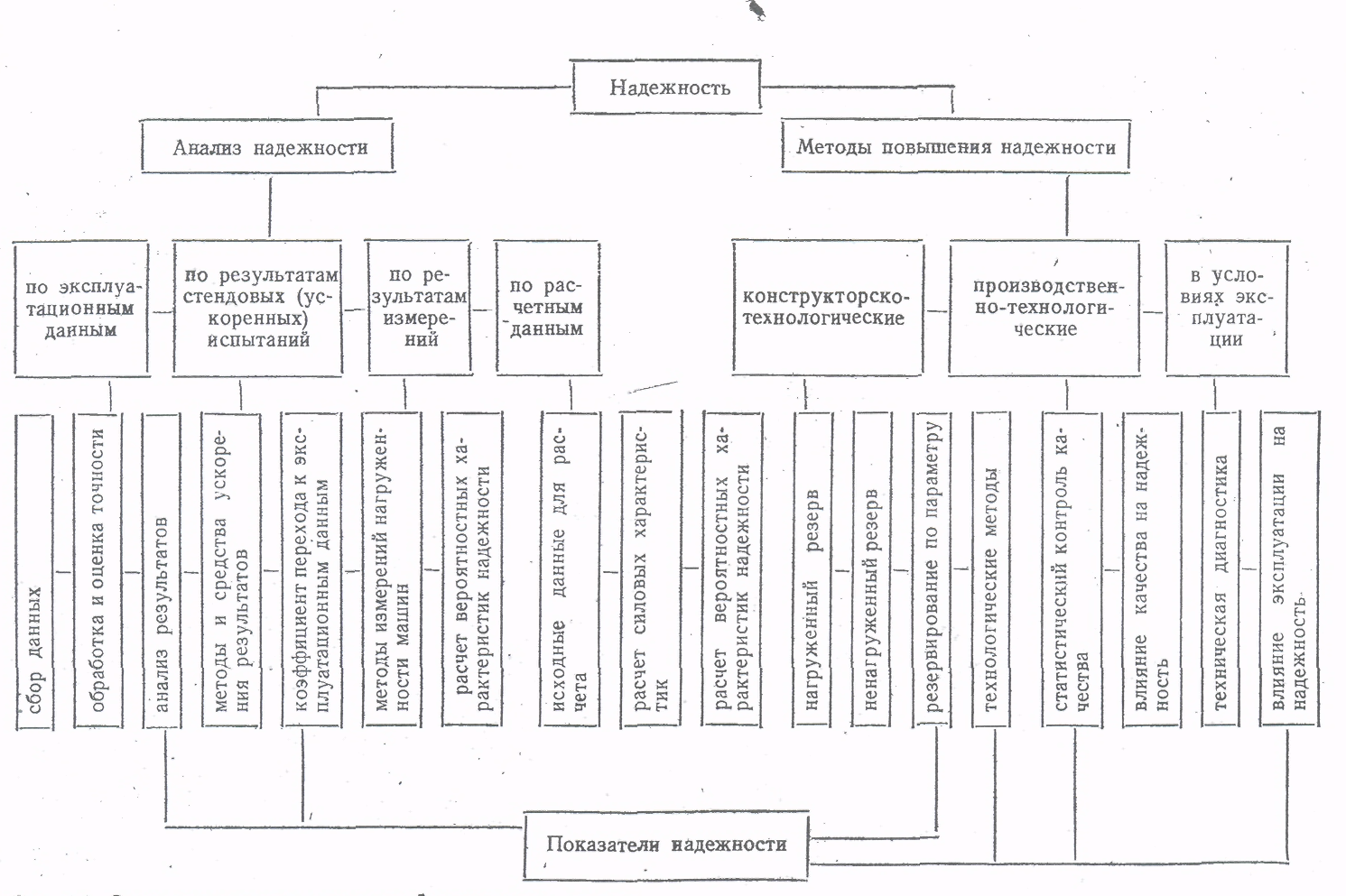



Рисунок 11. Схема определения показателей надежности машин.
Вероятность безотказной работы – это вероятность того, что в пределах заданной наработки отказ объекта не возникнет. Этот показатель может применяться для восстанавливаемых и невосстанавливаемых объектов. Выражается в долях единиц или в процентах, изменяется от 1 до 0.

Вероятность безотказной работы по статистическим данным по отказам оценивается выражением:

(t) = 1 - (65)

где (t) – статистическая оценка вероятности безотказной работы;

N_o – число объектов в начале испытания;

n(t) – число отказавших объектов за время t.

При большом числе объектов статистическая оценка (t) практически совпадает с вероятностью безотказной работы P(t)

Вероятность отказа – вероятность того, что при определенных условиях эксплуатации в заданном интервале времени или в пределах заданной наработки возникнет хотя бы один отказ. Вероятность отказа Q(t) при t=0 , изменяется от 0 до 1 и вычисляется по формуле:

Q(t) = 1 - P(t) (66)

Для статистического определения:

(t) = 1- (t) = (67)

С помощью приведенных формул можно построить так называемую функцию надежности, которая является убывающей (рисунок 12).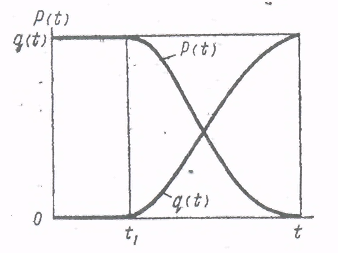



Рисунок 12. Зависимость вероятности безотказной работы и вероятности отказов от времени.
Для определения вероятности безотказной работы, как правило, используют данные, полученные в процессе эксплуатации, вместе с тем надежность объектов можно определить и по величине вероятности отказов, поскольку вероятности отказа и безотказной работы являются противоположными случайными событиями. Вероятность отказа Q(t) можно определить из выражения:

Q(t) = 1 – P(t). (68)

Вероятность безотказной работы машины зависит от числа деталей в машине и их вероятности безотказной работы: P_м = Р₁(t) Р₂(t) Р₃(t) Р_n(t) (по теореме умножения вероятностей).

Средняя наработка до отказа – математическое ожидание (среднее значение) наработки до первого отказа. Для невосстанавливаемых объектов средняя наработка до первого отказа равнозначна средней наработке до отказа.


Значение средней наработки до отказа Т_ср находят по уравнению:

Т_ср = ∑t_i (69)

где t_i наработка i-го объекта до отказа.

Точность определения средней наработки до отказа зависит от числа объектов, подвергшихся испытаниям на надежность.

Интенсивность отказов – условная плотность вероятности возникновения отказа невосстанавливаемого объекта, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник.

Из определения интенсивности отказов λ(t) следует, что

P(t) λ(t) ∆t = f (t) ∆t (70)

где P(t) –вероятность безотказной работы за время t; f(t) – плотность распределения наработки до отказа.

Из этого соотношения имеем

λ(t) = (71)

Интенсивность отказов может определяться по приближенной статистической формуле как отношение числа отказавших изделий в единицу времени к среднему числу изделий, работоспособных в данный момент времени.

Поток отказов. Для восстанавливаемых объектов, у которых вероятно многократное появление отказа, наработка на отказ – случайное событие. В этом случае отказавшие элементы заменяют на исправные и работоспособность объекта восстанавливается, т.е. наблюдается поток отказов и восстановлений. Поток отказов характеризуется двумя величинами: средним числом отказов m_ср(t) и параметром потока отказов ω_о(t).

Параметром потока отказов – называют плотность вероятности возникновения отказов восстанавливаемого объекта, определяемая для рассматриваемого момента времени или наработки.

Параметр потока отказов – это среднее число отказов восстанавливаемых объектов в единицу времени, взятое для рассматриваемого достаточно малого промежутка времени ∆t.

Наработка на отказ. Т представляет собой среднее значение наработки восстанавливаемых(ремонтируемых) объектов между отказами и показывает, какая наработка в среднем приходится на один отказ.

Наработка на отказ Т (среднее время безотказной работы) – величина обратная параметру потока отказов ω (t) для наработки от t₁ до t₂, определяемая по теоретической и статистической формулам.

Наработку на отказ статистически определяют отношением суммарной наработки восстанавливаемых объектов к суммарному числу отказов этих объектов.

По ГОСТ наработку на отказ определяют как отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки.

7.3 Показатели долговечности.

Долговечность количественно оценивается с помощью ресурса, как показателя, связанного с наработкой объекта и срока службы.

Средний ресурс (срок службы) - математическое ожидание ресурса (срока службы).

Назначенный ресурс-суммарная наработка объекта , по достижению которой эксплуатация должна быть прекращена независимо от его состояния (напр. авиационные двигатели).

Средний ресурс(срок службы) до ремонта Т_ДР –от начала эксплуатации до его первого ремонта.

Средний ресурс(срок службы) между ремонтами Т_МР –между смежными ремонтами.

Средний ресурс (срок службы) до списания Т_СП от начала эксплуатации до его списания, обусловленного предельным состоянием.

Гамма-процентный ресурс-наработка, в течение которой объект не достигнет предельного состояния с заданной вероятносьтю γ –процентов.Определяется экспериментально по данным о долговечности большой группы объектов. Гамма-процентный ресурс как оценочный показатель долговечности позволяет значительно сократить время испытаний, так как испытания ведут до исчерпания ресурса у сравнительно небольшого количества машин (10-20%), однако для получения достаточной точности оценки потребуется увеличить количество испытуемых машин.

Гамма-процентный срок службы – календарная продолжительность эксплуатации, в течение которой объект не достигнет предельного состояния с заданной вероятностью γ- процентов.
7.4 Показатели ремонтопригодности и сохраняемости.

Ремонтопригодность имеет следующие единичные количественные показатели.

Вероятность восстановления в заданное время, или вероятность своевременного восстановления< т.е. вероятность того, что время восстановления(время, потраченное на обнаружение , поиск причины отказа и устранение последствий отказа) не превысит заданного.

Среднее время восстановления, т.е. математическое ожидание времени восстановления работоспособности. При наличии статистических данных о длительности восстановления(для восстанавливаемых объектов) объектов среднее время восстановления Т_В определяют по формуле:

_В = ∑ t_{В i} (72)

где m - число обнаруженных и устраненных отказов объектов;

t_{В i} - время восстановления отказа.

В качестве характеристики рассеивания времени восстановления используется также дисперсия и среднее квадратическое отклонение.

Сохраняемость количественно оценивается с помощью следующих показателей, измеряемых в годах, месяцах и др. единицах.

Средний срок сохраняемости, т.е. математическое ожидание срока сохраняемости.

Гамма-процентный срок сохраняемости , т.е. срок сохраняемости, который будет достигнут объектом с заданной вероятностью γ. По кривой убыли при хранении объектов можно определить 90%-ный срок сохраняемости невосстанавливаемых объектов и средний срок сохраняемости, соответствующий времени в течение которого выходит 50% объектов. Эти показатели включаются в нормативно-техническую документацию, но не заменяют срок хранения, который также указывается в технических требованиях на объект.
7.5 Комплексные показатели надежности.

Коэффициент готовности – показывающий долю, которую составляет время работы объекта (наработка на отказ) от суммарного времени, расходуемого на работу и восстановление.

Таким образом, К_р характеризует свойства: ремонтопригодность и безотказность.

Коэффициент технического использования К_ти

Таким образом, К_ти более обобщенный показатель, чем К_г, служащий для оценки ремонтопригодности, т.к. учитывает простои в ремонте и ТО.

- средняя суммарная трудоемкость ремонта (или ТО) – математическое ожидание суммарных трудозатрат на ремонт (или ТО);

- коэффициент восстановления ресурса, равный отношению среднего ресурса капитально отремонтированных машин к их среднему ресурсу до первого капитального ремонта. Он должен быть менее 80%.

Список рекомендуемой литературы

1. Ермолов Л.С., Кряжков В.М., Черкун В.Е., - Основы надежности сельскохозяйственной техники. М.: Колос, 1982

2. Селиванов А.И., Артемьев Ю.Н. – Теоретические основы ремонта и надежности сельскохозяйственной техники. М. Колос, 1978

3.Авдеев М.В., Воловик Е.Л., Ульман И.Е. – Технология ремонта машин и оборудования. М.: Агропромиздат, 1986
Контрольные вопросы:

1. Что такое квалиметрия?

2. Какие показатели применяются при оценке качества продукции?

3. Как определяется вероятность безотказной работы, вероятность отказа, интенсивность отказа, поток отказов, наработка на отказ?

4. Какие показатели используются для оценки долговечности машин?

5. Какие показатели используются для оценки ремонтопригодности и сохраняемости?

6. Какие комплексные показатели надежности используются для оценки надежности машин?

Тема №9,10 Частота отказов. Интенсивность отказов.

Цель: Изучение основных понятий теории надежности технологических машин.

План:

1. Плотность распределения времени работы изделия до отказа. Среднее время безотказной работы.

2. Выражение вероятности и частоты отказов через интенсивность отказов.
9.1 Среднее время безотказной работы.

Сложная машина – это система, состоящая из большого числа элементов (деталей). Отказ любого элемента отражается на работоспособности в целом всей машины. В обычных машинах мы имеем последовательное соединение элементов (привод от двигателя к ведущим колесам).

Если выйдет из строя шестерня, подшипник, муфта, то весь привод перестанет функционировать.

При известной вероятности безотказной работы P_i(t) каждого элемента можно подсчитать безотказность всего привода.

Вероятность безотказной работы такой системы равна произведению вероятностей безотказной работы отдельных ее элементов (по теории умножения вероятностей независимых событий).

Рм(t) = P₁(t) P₂(t)….P_n(t ) = (73)

В результате сложная система, состоящая из элементов высокой надежности, может иметь очень низкую надежность.

Из формулы (73) следует, что наиболее простой путь повышения безотказности машины заключается в повышении безотказности тех ее элементов, отказ которых вызывает выход из строя машины. Поскольку надежность машины определяет самый слабый элемент, то выявление его и есть важнейший этап в разработке мероприятий по обеспечению повышения надежности объекта.

Однако повышение надежности сложных систем, может быть осуществлена не только за счет увеличения надежности их элементов. Если принять, например, что система состоит из шести элементов

Р_с(t) = = 0,9×0,8×0,9×0,9×0,8×0,7 = 0,33, (74)

то вероятность безотказной работы всей системы за период t составит только Р_с = 0,33. При этом вероятность безотказной работы всей системы всегда меньше, чем вероятность безотказной работы входящего в нее элемента с наименьшим значением P_i(t). С увеличением количества элементов, обеспечивающих функционирование системы, вероятность безотказной работы системы снижается даже в том случае, когда вероятность безотказной работы каждого элемента достаточно высока (при n→∞, P_c(t)→0).

Иногда по своим техническим данным машины (агрегаты, узлы, детали) не могут обеспечить необходимых показателей надежности. В этом случае применяют резервирование (ввод избыточных агрегатов, узлов или деталей), которое является эффективным способом повышения надежности машин.

В теории надежности различают два метода резервирования (общий и раздельный) и два способа включения резерва (постоянный и путем замещения).

При общем резервировании резервируется объект в целом, при раздельном – отдельные элементы объекта или их группы.

Постоянное резервирование состоит в том, что резервные элементы участвуют в функционировании объекта наравне с основными. Если же резерв включается в работу после того, как вышел из строя основной элемент (агрегат, узел, деталь), то такое резервирование называют резервирование замещением.

9.2 Выражение вероятности и частоты отказов через интенсивность отказов.

Для повышения надежности системы из n последовательно соединенных элементов параллельно к ней подключают m точно таких же систем. В этом случае вероятность безотказной работы резервированной системы можно определить (при одинаковой надежности всех элементов) по формуле:

Р_с(t) = 1 - [1 - Pⁿ (t) ]^m (75)

Если величина P(t) поддерживается на одном уровне, а число последовательных элементов (n) в цепи стремится к бесконечности, то вероятность безотказной работы уменьшается до нуля даже в том случае, если количество параллельных цепей стремится к бесконечности.

Вероятность безотказной работы системы с раздельным резервированием определяется по формуле:

Р 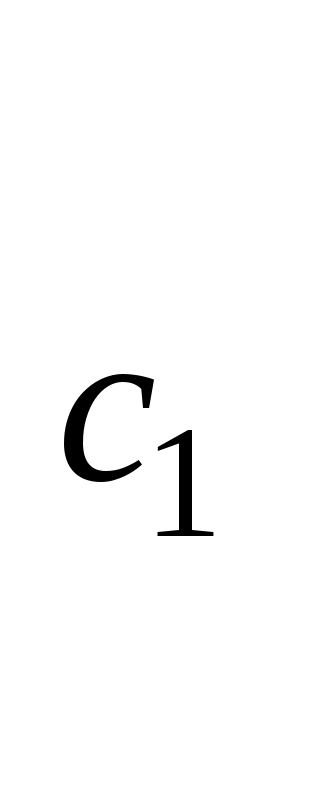(t) = [1 – (1 – P(t)^m )]ⁿ (76)

В этом случае вероятность безотказной работы Р(t) стремится к единице при неограниченном увеличении числа параллельных элементов, даже когда количество последовательных цепей стремится к бесконечности.

Вероятность отказа всех элементов (основного и резервных) по теореме умножения вероятностей.

Q_ст (t) = Q₁ (t)*Q₂ (t)* *Q_n (t) = Q_i (t), (77)

где Q_i (t) - вероятность отказа элемента i.

Вероятность безотказной работы Р_ст(t) = 1 - Q_ст (t).

Если элементы одинаковы, то Р_ст(t) = 1 – Q₁ⁿ (t)

Например, если Q = 0.01 и n = 2 (дублирование), то Р_ст = 0,9999, если же

Q = 0.01 и n = 3 (двойное дублирование), то Р_ст = 0,999999.

Таким образом, в системе с последовательным соединением элементов вероятность безотказной работы определяют перемножением вероятностей безотказной работы элементов, а в системах с параллельным – вероятность отказа перемножением вероятностей отказа элементов.

Для основного случая экспоненциального распределения отказов при малых значениях λt, то есть при достаточно высокой надежности элементов, вероятность отказа системы равна

Q_ст(t) ≈ 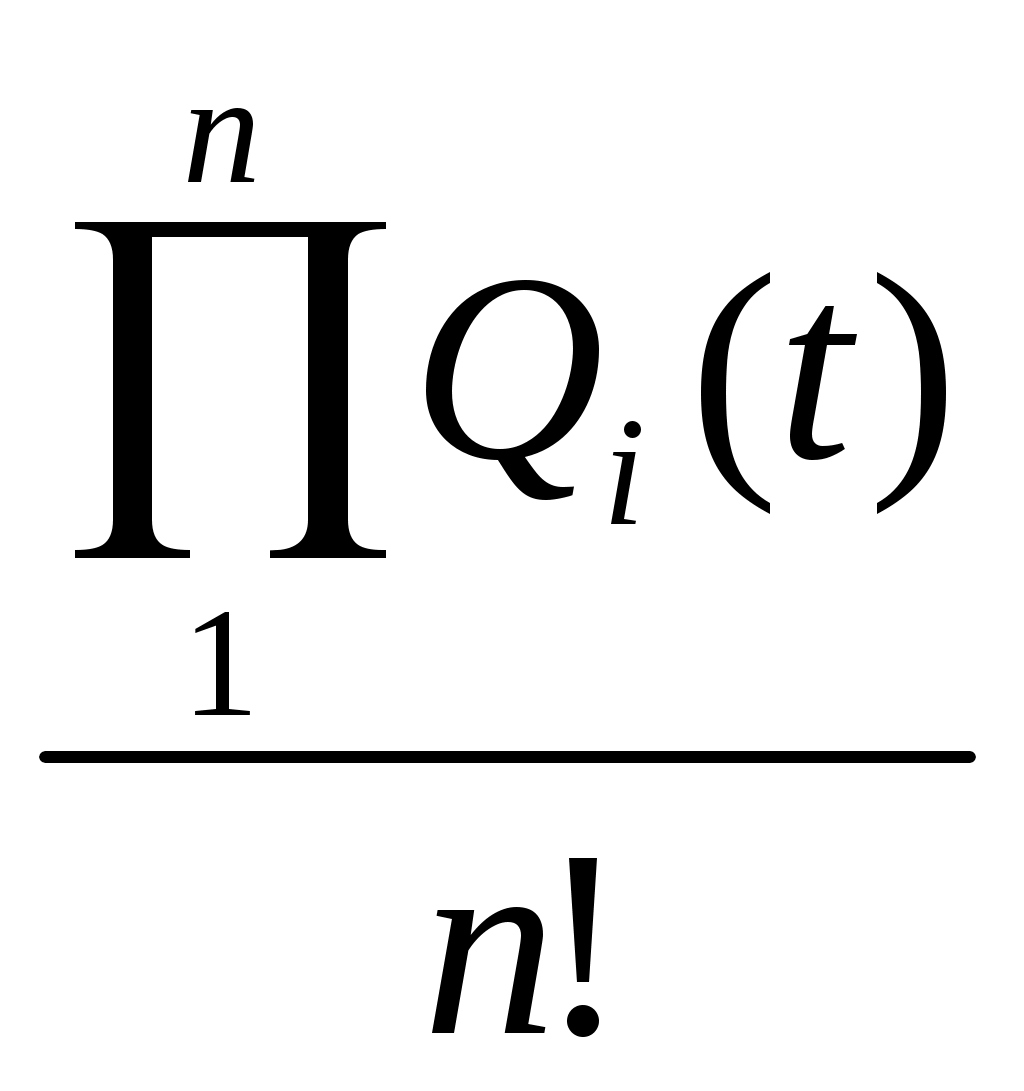≈ 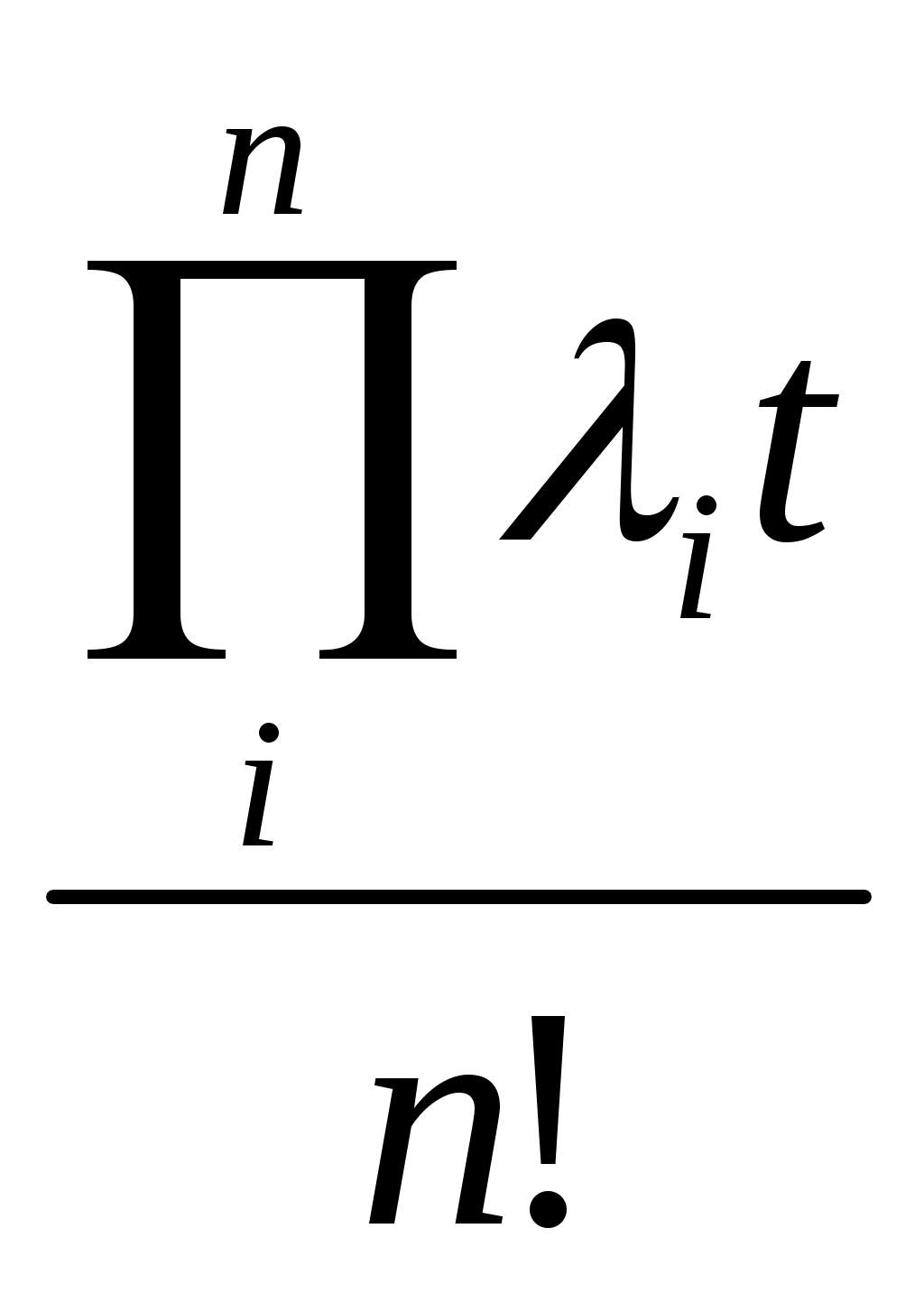. (78)
Если все элементы одинаковы, то

Q_ст(t) ≈ ≈ (79)
Для поддержания высокой надежности резервированных систем отказавшие элементы необходимо восстанавливать или заменять.

Эффективность разных способов резервирования рассмотрим на основной системе из четырех последовательно соединенных элементов с вероятностью безотказной работы каждого 0,9.

Вероятность безотказной работы системы без резервирования (рис. 13,а )

Р_ст (t) = Р (t) =-0.9⁴ ≈ 0.65 и Q_ст(t) ≈ 0.35, (80)

дублированной системы с постоянным резервом в виде такой же системы (рисунок 13,б)

Р_ст(t) = 1 – Q 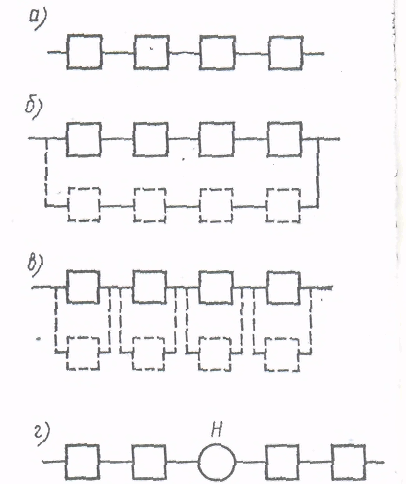(t) = 1 – 0.35² ≈ 0.88, (81)



Рисунок 13. Система резервирования.

а – основная; б – с общим резервированием; в – с поэлементным резервированием; г – с накопителем.

Дублированной системы с ненагруженным резервом и вполне надежным переключателем

Р_ст(t) = 1 - = 1- ≈ 0,94, (82)

системы с независимым постоянным дублированием каждого элемента (рисунок 13 , в)

Р_ст = [1 - Q (t)]⁴ = (1 – 0,1²)⁴ = 0,96, (83)

Такой же системы с независимым ненагруженным дублированием

Р_ст = [1 - ]⁴ = [1 - ]⁴ ≈ 0,98 (84)

Если систему,например автоматическую линию, рассматривать как технологическую и поставить в середине накопитель высокой надежности (рисунок 13, г), то вероятность безотказной работы поднимется с 0,65 до величины, несколько меньше 0,81.

Приведенный пример наглядно показывает, что поэлементное резервирование гораздо эффективнее, чем общее, а резервирование замещением при совершенно надежном переключении эффективнее, чем постоянное.

Список рекомендуемой литературы

1.Ермолов Л.С., Кряжков В.М., Черкун В.Е., - Основы надежности сельскохозяйственной техники. М.: Колос, 1982

2.Ю.Н. Артемьев Качество ремонта и надежность машин в сельском хозяйстве. М, Колос, 1981

3.Д.Н.Решетов, А.С. Иванов, В.З. Фадеев Надежность машины М, Высшая школа, 1988.

4.В.И. Прейсман. Основы надежности сельскохозяйственной техники. Киев-Донецк «Вица школа», 1979.

5.Селиванов А.И., Артемьев Ю.Н. – Теоретические основы ремонта и надежности сельскохозяйственной техники. М. Колос, 1978

6.Авдеев М.В., Воловик Е.Л., Ульман И.Е. – Технология ремонта машин и оборудования. М.: Агропромиздат, 1986
Контрольные вопросы:

1. По какой формуле определяется вероятность безотказной работы системы, состоящей из большого числа элементов (деталей)?

2. Для какой цели используется резервирование?

3. Какие методы резервирования используются в теории надежности?

4. В чем заключается суть постоянного резервирования и резервирования замещением?