лекции. 3 Лекции НСХТ. Лекции по дисциплине Надежность сельскохозяйственной техники Тема 1. Введение. Цель и задачи курса. Цель Изучение теории надежности транспортной техники План

• Название: Лекции по дисциплине Надежность сельскохозяйственной техники Тема 1. Введение. Цель и задачи курса. Цель Изучение теории надежности транспортной техники План
• Анкор: лекции
• Дата: 18.05.2023
• Размер: 2.82 Mb.
• Имя файла: 3 Лекции НСХТ.doc
• Тип: Лекции; #1140950
• страница: 3 из 7

5.2. Распределение случайных величин.

Распределение случайных величин - это совокупность значений случайных величин, расположенных в возрастающем порядке, с указанием их вероятностей (для теоретических распределений) и частостей (для эмпирических распределений).

Закон распределения случайной величины – это всякое соотношение, устанавливающее связь между возможными значениями случайных величин и соответствующими этим значениям вероятностями или частостями.

Дискретные (прерывные) случайные величины Х могут принимать только ряд отдельных значений х₁, х₂,..х_n, каждому из которых соответствует некоторое значение вероятности Р₁,Р₂,…,Р_n.

Рассматривая появление любого из перечисленных значений прерывной случайной величины как события, заметим, что эти события образуют полную группу несовместных случайных событий, а следовательно, сумма вероятностей всех возможных значений прерывистой случайной величины равна единице:

Р₁ + Р₂ + + Р_n = 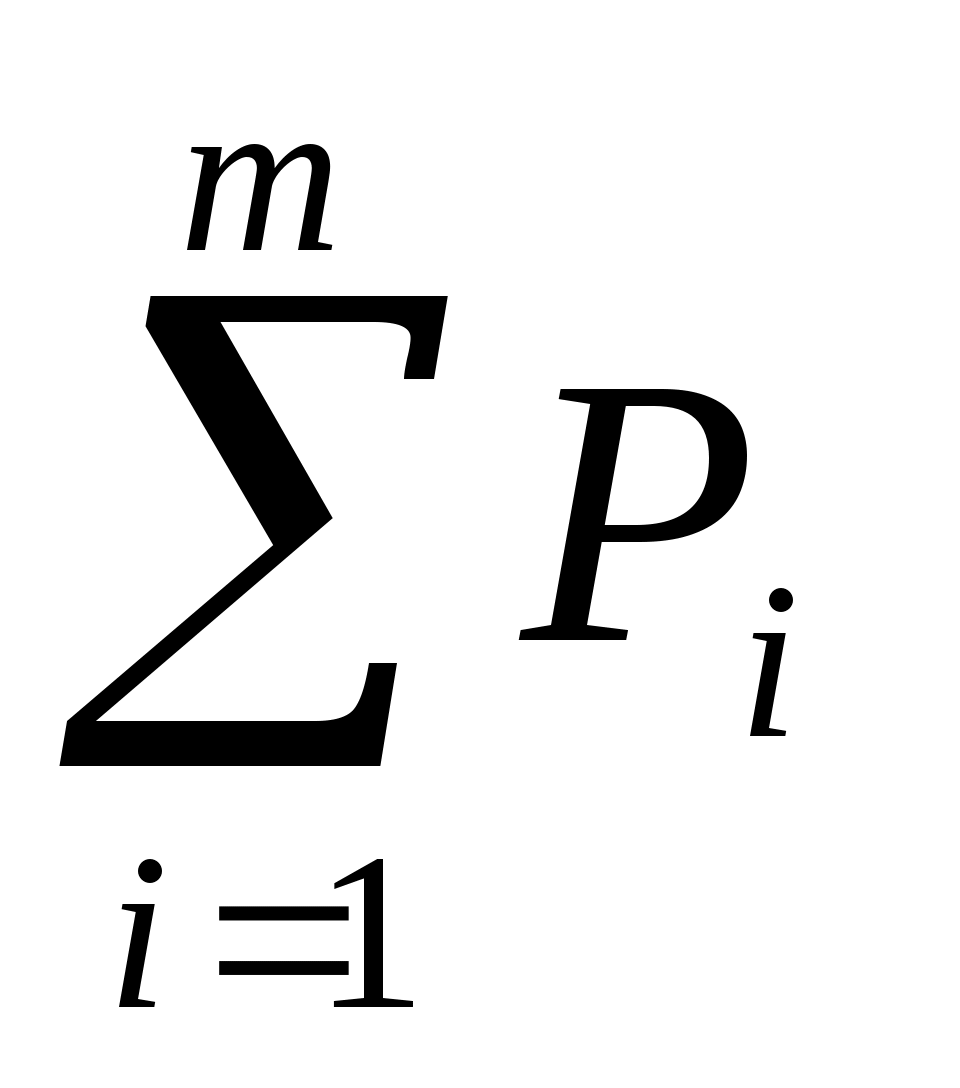= 1 (25)

Распределение прерывной случайной величины может быть представлено в виде таблицы, называемой рядом распределения (таблица 1) или графически многоугольником распределения (рисунок 1).

Таблица 1. Ряд распределения случайной величины

Значения случайной величины Х	х1	х2	…	хn
Вероятность Р (Х = хi ) = Р	Р1	Р2	…	Рn

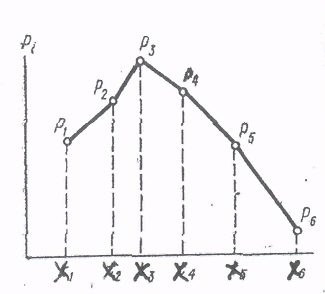Рисунок 1.Многоугольник распределения прерывной случайной величины
При графическом представлении (см. рисунок 1) по оси абсцисс откладывают значения случайной величины х_i , а по оси ординат – вероятность Р_i, соответствующие этим значениям.

Ряд распределения и многоугольник удобны только для дискретных случайных величин. В случае непрерывной случайной величины, которая имеет бесчисленное множество значений, такая форма непригодна. В этом случае используется не вероятность события P(X=x_i), а вероятность события P(Xx_i), т.е. вероятность, что случайная величина примет значение меньше какого-либо наперед выбранного значения -.

Площадь элементарного прямоугольника, равную произведению f(x)dx, называют элементом вероятности (рисунок 2). Для определения вероятности событий Р(Х < х) необходимо вычислить площадь, заключенную между кривой и осью Х в интервале от ∞ до х, т.е.сложить все элементы вероятностей в интервале от ∞ до х.

F(x) 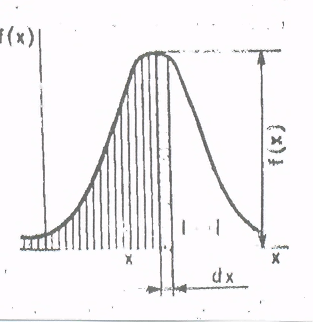(26)


Рисунок 2. График функции f(x) для непрерывной случайной величины
Функция (интегральный закон) распределения случайной величины - наиболее универсальная характеристика как дискретных (прерывных), так и непрерывных случайных величин.

Если Х – случайная величина, а х - некоторое действительное число, то вероятность того, что Х < х:

F( x ) = P ( X < x ), (27)

где F(x) - функция распределения.

Функцию распределения можно представить в виде графика, если по оси абсцисс откладывать значение x_i , а по оси ординат – значения F(x).

Для дискретной случайной величины график функции распределения будет иметь вид ступенчатой кривой (рисунок 3).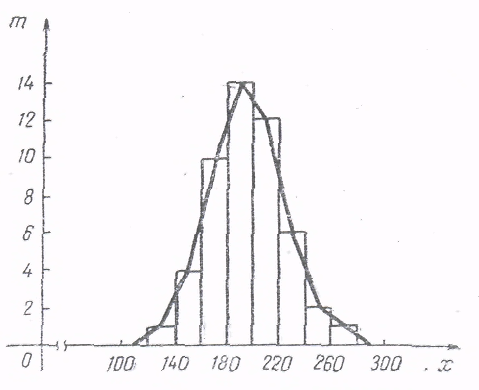



Рисунок 3. Полигон и гистограмма
Функцию распределения непрерывной случайной величины изображают плавной кривой. При любом значении х 0 < F(x) < 1.

В эмпирических распределениях возможные значения случайных величин оцениваются частотами или частостями, полученными в результате испытаний или опытов.

На практике при изучении непрерывных случайных величин их полученные значения делят на интервалы или разряды. После этого подсчитывают частоты по разрядам.

В таблице эмпирического распределения случайной величины указывают интервалы значений x_i, частоту m_i и чаcтость W_i = m_i/ N.

Эмпирическое распределение может быть изображено в виде ступенчатого графика, называемого гистограммой, или в виде ломаной линии, называемой полигоном.

О характере распределения непрерывной случайной величины в окрестностях различных точек можно судить на основании особой функции, называемой плотностью распределения.

Плотность распределения непрерывной случайной величины – это производная от функции распределения непрерывной случайной величины:

f(x) = (28)

Для дискретной величины функция плотности распределения не существует.

Графически плотность распределения представляет собой кривую распределения случайных величин.

Плотность распределения характеризуется следующими основными свойствами.

1. Она неотрицательная функция от х вследствие того, что F(х) –неубывающая функция.

2. Площадь, ограниченная кривой f(x) и осью абсцисс (интеграл от плотности распределения в бесконечных пределах), равна единице, т.е.

f(x) dx = 1 (29)

При изучении случайных величин часто достаточно знать числовые характеристики распределения случайной величины.
5.3 Характеристики распределения случайной величины.

Числовые характеристики, полученные по результатам опытов, называются статистическими характеристиками случайной величины.

Теоретические характеристики, определенные по теоретическому закону распределения, называются параметрами распределения:

Основными статистическими характеристиками случайных величин, изучаемых в теории надежности, служат среднее арифметическое и среднее квадратическое отклонение.

1) Среднее арифметическое - это частное от деления суммы измеренных значений на число слагаемых этой суммы, т.е. на число испытаний (опытов).

= = (30)

Средняя взвешенная величина определяется по формуле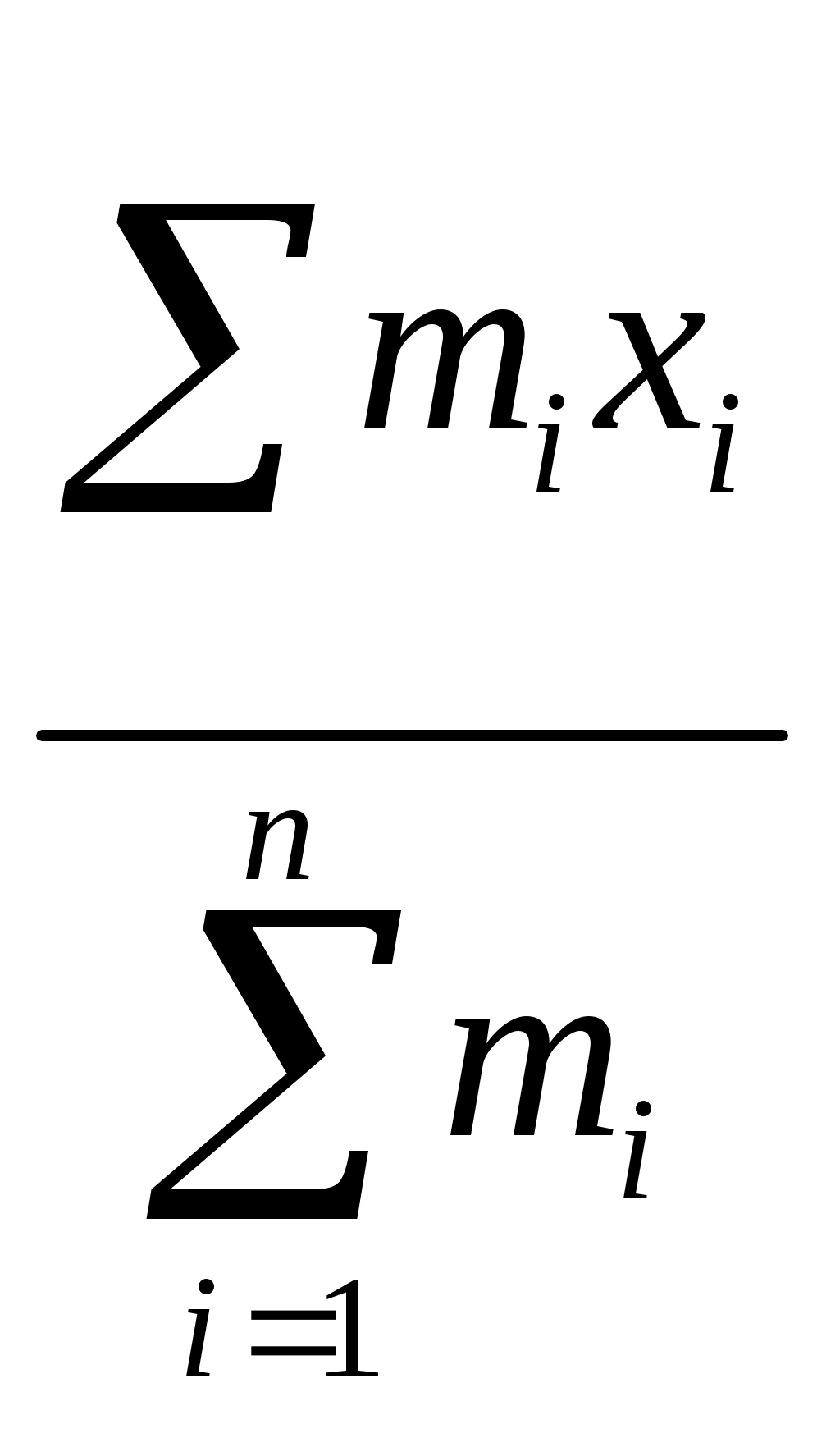

= = , (31)

где m_i –частота; = N –число всех зафиксированных значений x_i.

Средняя взвешенная подсчитывается также сумма произведений значений случайной величины x _i на соответствующие им частости m_i / N , т.е.

= W ₁x ₁+W ₂x ₂+ + W _nx_n = (32)

При достаточно большом числе испытаний N частости приближенно равны соответствующей вероятности

W₁ ≈ P₁ ; W₂ ≈P₂ ; W_n ≈ P_n; (33)

Заменив в формуле относительные частоты соответствующими вероятностями, получим для дискретной случайной величины равенство для определения математического ожидания:

MX ≈ P₁ x₁+ P₂ x₂ + + P_n x_n= ∑P_i x_i (34)

2) Размах R распределения (диапазон распределения) в эмпирической совокупности – разность между максимальным и минимальным из значений случайной величины x_i ,полученных в результате испытаний.

Им пользуются в эмпирических распределениях как мерой рассеивания при малом числе испытаний(N < 10).

Рассеивание случайной величины наиболее часто измеряют дисперсией(рассеиванием) и средним квадратическим отклонением.

3) Эмпирическая дисперсия S² - величина рассеивания зафиксированных значений вокруг их среднего значения. При малом числе наблюдений т.е. при N < 25, S² = (35)

При N > 25 S² = 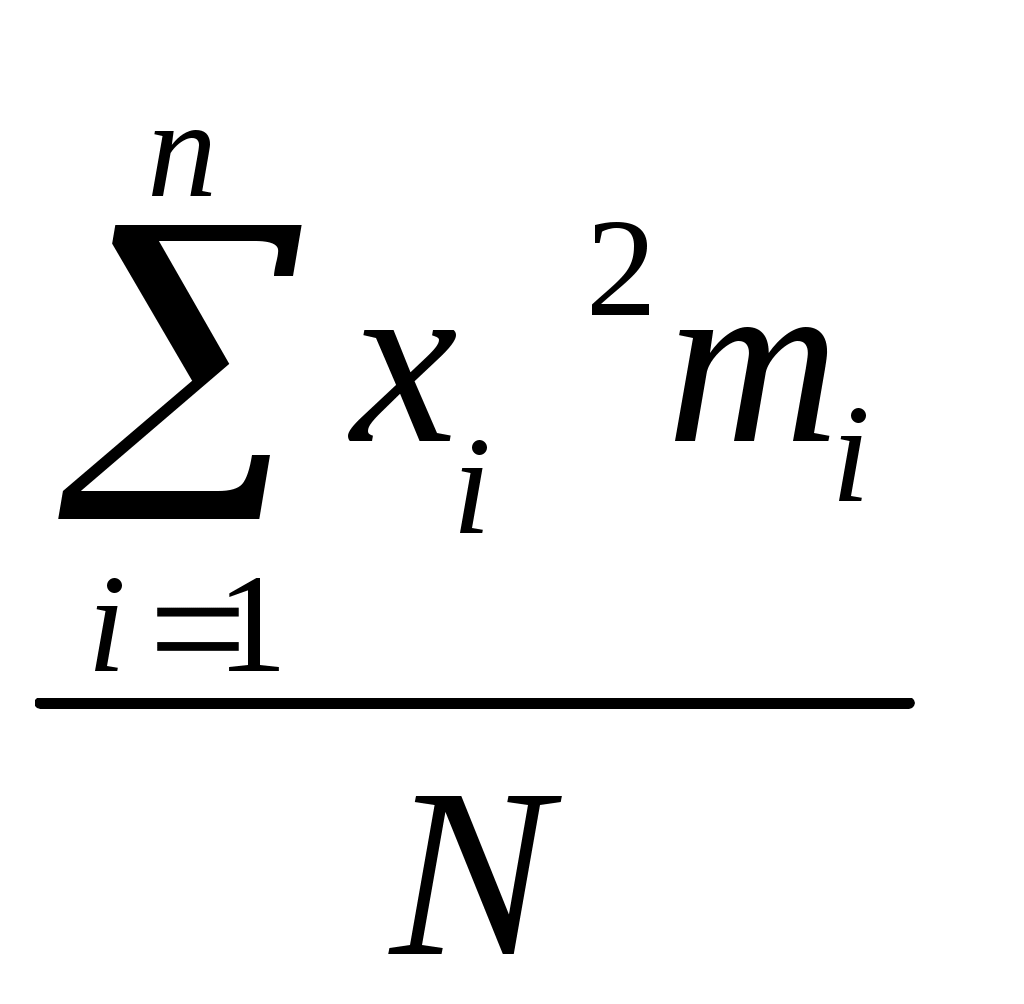= a₂ - , (36)

где а₂ = (37)

Эмпирическое среднее квадратическое отклонение и среднее квадратическое отклонение (стандарт) будут соответственно равны корням квадратным из дисперсии S² и из DX.

Размерности S и σ совпадают с размерностью самой случайной величины х.

σ = и определяет ширину кривой распределения.

4) Мода М₀ эмпирической совокупности - это значение непрерывной случайной величины х_i , соответствующее наибольшей ординате полигона распределения (рисунок 4а). За моду прерывной случайной величины принимают значение, имеющее наибольшую вероятность.

5) Мода М₀₀ теоретического распределения случайной величины – это такое значение x_i, которое соответствует максимальному значению плотности распределения f(x) (рисунок 4б).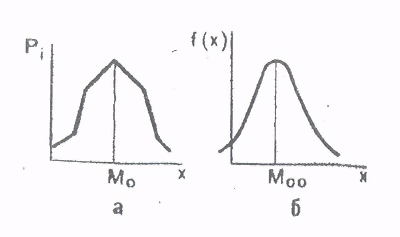



Рисунок 4. Мода случайных величин:

а – дискретной (прерывной); б - непрерывной

6) Медиана Мео теоретического распределения – это такое значение x_i, при котором вероятность больших или меньших его значений одинакова, т.е. это ордината кривой распределения, которая делит площадь под ней на две равные части (рисунок 5).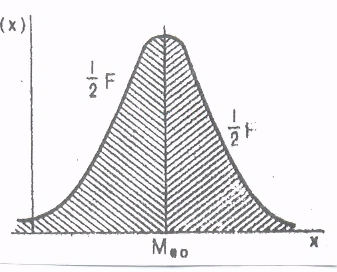



Рисунок 5. Медиана непрерывной случайной величины
Разброс случайной величины относительно центра распределения (среднеарифметической, математического ожидания, моды или медианы) характеризуется мерами рассеивания.

К мерам рассеивания относятся: размах, дисперсия (рассеивание), среднее квадратическое отклонение (стандарт) и коэффициент вариации.

7) Эмпирическое среднее квадратическое отклонение и среднее квадратическое отклонение (стандарт) будут соответственно равны корням квадратным из дисперсии S² и из DX, взятых с положительным знаком.

При малом числе наблюдений, т.е.при N < 25

S = (38)

При N > 25

S = (39)

Размерности S и σ совпадают с размерностью самой случайной величины х. Если при вычислениях исходят не из отклонений от среднего арифметического, а из непосредственно измеренных величин, то

S = (40)

σ = и определяет ширину кривой распределения.

Дисперсия суммы (разности) взаимно независимых случайных величин равна сумме (разности) их дисперсий.

σ² ₌σ ₁² + σ + + σ = (41)

Среднее квадратическое отклонение суммы конечного числа взаимно независимых величин равно корню квадратному из суммы квадратов средних квадратических отклонений этих величин.

Среднее квадратическое отклонение величины среднего арифметического значения (cредняя ошибка) составляет 1/N от и вычисляется как: σ _X= (42)

Cовокупность не содержит грубых погрешностей согласно критерию Райта в том случае, если | x_i | ≤ 3σ (43)

где | x_i | - максимальное по абсолютной величине отклонение, равное |x_max - |.

При обработке результатов испытаний может возникнуть необходимость сравнить различные распределения, а также рассеивание разнородных величин. В качестве отвлеченной меры рассеивания, не зависящей от единиц измерения сравниваемых величин, принимается коэффициент вариации или изменчивости ν_x.

8) Для сравнения рассеивания разнородных величин дисперсия и стандарт не могут быть использованы. Для этого применяется коэффициент вариации υ_x.

Для эмпирического распределения υ_x=S/X – он показывает насколько велико рассеивание по сравнению со средним значением случайной величины.

Для теоретического распределения υ_x=/МХ (МХ – математическое ожидание).

Коэффициент вариации может быть выражен в процентах: υ_x=S/ 100%.
5.4 Статистическая оценка надежности. Законы распределения случайной величины, характеризующие надежность.

Сбор, обработка и анализ информации о надежности связаны с необходимостью исследования случайных событий.

Статистическая совокупность – это такая совокупность, которая состоит из однородных объектов, обладающих качественной общностью.

Генеральная или общая совокупность – это совокупность объектов, содержащая все исследуемые объекты.

Выборка или выборочная совокупность – определенное число объектов, отобранных из исследуемой совокупности для получения сведений о генеральной совокупности.

Выборка должна быть представительной, т.е. такой, чтобы каждый объект был отобран случайно и все они имели одинаковую вероятность попасть в выборку

Объем выборки – число объектов наблюдений, составляющих выборку.

Чаще всего встречаются со следующими распределениями (законами распределения): нормальным и его разновидностями (усеченным нормальным, логарифмически нормальным); экспоненциальным (показательным); Релея; Вейбулла – Гнеденко; гамма-распределением; Пуассона; биноминальным.

Закон нормального распределенияполучил наибольшее распространение в технических приложениях(нормальный закон Гаусса). Он играет важную роль в теории вероятности и теории надежности. Этому закону подчиняются многие случайные величины массовых явлений, на которые оказывает большое число факторов, равнозначных по своим значениям (напр. износы, измерения большого числа деталей микрометрическими методами).

Плотность нормального распределения непрерывной случайной величины выглядит так: f(x) = exp(- ), (44)

где среднее квадратическое отклонение случайной величины х ;

е – основание натурального логарифма, равное 2,7183;

х - случайная величина (- ∞< х < +∞);

- среднее арифметическое значение(математическое ожидание) случайной величины х.

Дифференциальная кривая, соответствующая ЗНР, симметрична относительно ординаты в точке х = 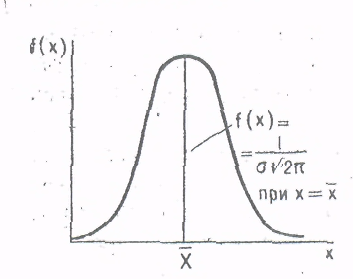, называемой центром распределения, и имеет колоколообразный вид (рисунок 6).


Рисунок 6. Нормальный закон распределения случайных величин.
Случайная величина, подчиняющаяся закону нормального распределения, имеет три следующих свойства; одинаковые положительные и отрицательные отклонения от средней арифметической равновозможны; меньшие отклонения более вероятные, чем большие; весьма большие отклонения от маловероятны. Для подсчета вероятности того, что случайная величина находится в тех или иных пределах, пользуются интегралом Ф(t), значения которого приводятся в таблицах, имеющихся в литературе по математической статистике.

Интегральная функция закона нормального распределения записывается следующим образом:

F(x) = = (45)

Для подсчета того, что случайная величина находится в тех или иных пределах, пользуются интегралом Ф(t), значения которого приводятся в таблицах, имеющихся в литературе по математической статистике и учебниках по надежности машин.

Табличный интеграл Ф(t) соответствует площади под кривой, заключенной между осью симметрии кривой и ординатой, соответствующей значению t, и непосредственно дает вероятность того, что значение случайной величины находится в пределах от 0 до t.

Так, например, для х = 3 (t = 3) из таблиц находим Ф(t) = 0,49865, т.е. для 2Ф(3) = 0,9973 ≈ 1.Таким образом, характерной особенностью нормального распределения является то, что вероятность или частость значений х , заключенных в пределах от -3σ до +3σ, составляет 0,9973б, то есть близка к единице.

Кривые распределения, подчиняющиеся ЗНР, могут характеризоваться также асимметрией А (рисунок 7а) и эксцессом Е (рисунок 7б).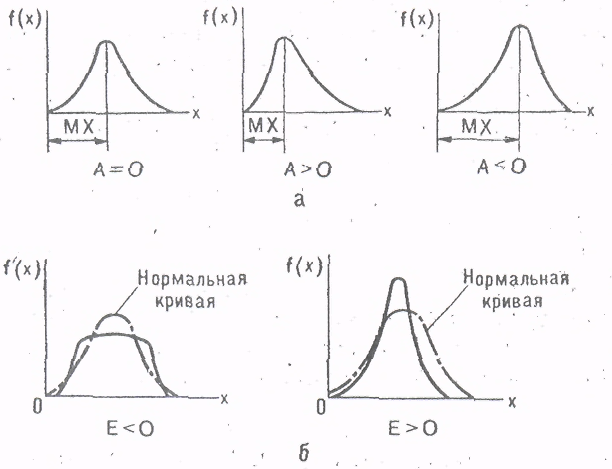


Рисунок 7. Кривые распределения (а – с асимметрией; б – с эксцессом)
При А = 0, кривая симметрична; при А>0 кривая имеет положительную асимметрию; при А<0 – отрицательную.

Эксцесс характеризует крутизну кривой. При Е<0 наблюдается отрицательный эксцесс; при Е>0 – положительный при Е=0 эксцесс отсуствует (нормальная кривая).

Для закона усеченного нормального распределения – случайная величина х с двух сторон ограничена определенными значениями.

Логарифмическое нормальное распределение – это когда десятичный логарифм случайной величины х распределяется по нормальному закону.

Экспоненциальное распределение (показательное).

Дифференциальная функция экспоненциального закона распределения случайных величин (рисунок 8а) при x ≥ 1 имеет вид:

f(x) = λe^-λx = λ exp ( λx ) (46)

где λ - постоянная величина (коэффициент).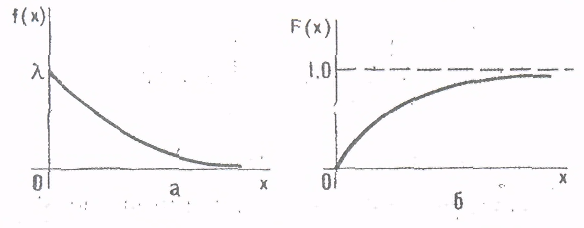



Рисунок 8. Экспоненциальный закон распределения случайных величин:

а – плотность распределения; б – функция распределения.
Интегральная функция (рисунок 8б)

F(x) = = = 1 – e^-λx = 1 – exp(-λ x) (47)

Математическое ожидание случайной величины х, имеющей показательное распределение, - это величина, обратная коэффициенту λ.

У показательного распределения математическое ожидание и среднеквадратичное отклонение равны.

Распределение Релея - распределение положительной случайной величины происходит с плотностью распределения вида:

f(x) = exp (- ) (48)

Функцию распределения Релея находят по уравнению:

F(x) = 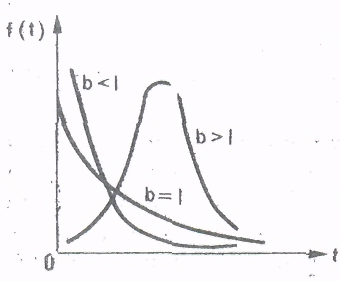1 – exp(- ) (49)



Рисунок 9. Распределение Вейбулла-Гнеденко

Распределение Вейбулла-Гнеденко (рисунок 9)имеет следующую плотность распределения:

f(x) = ( )^b-1 exp (- )^b (50)

где b и a - параметры распределения.

При b = 1 распределение Вейбулла-Гнеденко совпадает с экспоненциальным распределением, а при b = 2 – с распределением Релея.

Интегральная функция распределения: F(t) = 1 – exp [ - ( )^b] (51)

Распределение Пуассона.. Распределение дискретных случайных величин по закону распределения Пуассона. Например, если в начальный период эксплуатации изделия (период приработки) поток отказов нестационарный, то после окончания процесса приработки поток отказов становится стационарным и, следовательно, простейшим (пуассоновским).

Вероятность частот событий находят по формуле:

Р_m = = e^—a (52)

где m – частота данного события, mi – m – факториал, n –число испытаний, Р – вероятность события при одном испытании, а=nP – математическое ожидание случайных величин. Для распределения Пуассона дисперсия равна математическому ожиданию.
5.5 Критерии согласия.

При обработке эмпирических данных, чтобы иметь полное представление об изменениях случайной величины, надо знать закон ее распределения. Поэтому на основании экспериментальных данных выдвигают гипотезу о законе распределения случайной величины. Делают это обычно по величине коэффициента вариации υ. Если υ0,33 предлагают ЗНР, если υ0,50 – ЗРВ.

Смысл проверки «согласия» заключается в определении степени расхождения опытной и теоретической вероятности. Мерой совпадения или расхождения служат критерии согласия. Критерии согласия являются случайными величинами и, следовательно, подчиняются определенному закону распределения. Поэтому по величине критерия согласия и определяют вероятность совпадения опытной и теоретической функций. В качестве примера согласия в теории надежности пользуются двумя:

- Критерий Колмогорова -  определяю: = Dmax , (53)

где D_max – наибольшая абсолютная разность между накопленными эмпирическими и теоретическими частостями

D_max = , (54)

N – число наблюдений опытов.

По вычисленному  определяют вероятность Р() подчинения его закону распределения. В практических расчетах считается, что если  ≤ 1, то считают, что согласие между эмпирическим и теоретическим законами распределения хорошее. Более точно оценка согласия выполняется по функции вероятности Р(λ).

- Критерий Пирсона. При большом числе наблюдений сводит ошибки к минимуму. Он определяется из выражения: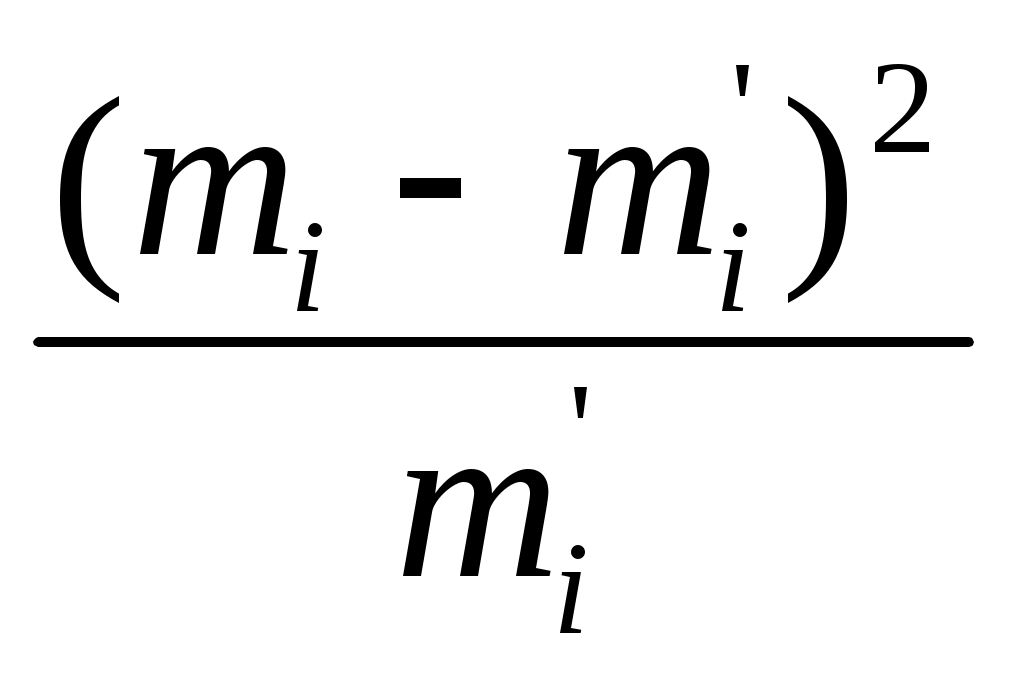

= ∑ (55)

m_i – опытная частота (количество случаев) в i-м интервале статистического ряда; n_i – принятое количество интервалов; =N[F(t_i+1) – F(t_i)] – теоретическая частота.

Частоты, значение которых менее 5, следует объединить.

После нахождения определяем число степеней свободы:

K = n₁ – r – 1, (56)

где k – число степеней свободы; n_{1 –} число сравниваемых частот;

r – число параметров теоретической функции распределения.

5.6 Доверительная вероятность оценки точности определения математического ожидания и дисперсии.

Основные параметры теоретических распределений –математическое ожидание MX и дисперсия DX. Вычисленные по эмпирическому распределению среднее значение и дисперсия S² являются точечными оценками для теоретических значений MX и DX, и при достаточно большом числе опытов можно считать , что = MX , а S² = DX.. В связи с тем, что объем выборки , как правило, невелик, необходимо пользоваться интервальными оценками, которые определяются двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надежность оценок, т.е. позволяют найти к каким ошибкам может привести замена значения теоретического параметра m статистической характеристикой m^*. Известно, что m^* тем точнее определяет параметр m, чем меньше абсолютная величина разности | m –m^* |, то есть δ> 0 и | m –m^* | <δ, чем меньше δ, тем оценка точнее. Таким образом ,положительное число δ характеризует точность оценки.

Однако статистические методы не позволяют категорически утверждать, что оценка m^* удовлетворяет неравенству | m –m^* | <δ, можно лишь говорить о вероятности α, при которой это неравенство справедливо.

Доверительной вероятностью (надежностью) оценки m по m^* называют вероятность α при которой выполняется неравенство | m –m^* | <α.

Обычно надежность оценки задается наперед, в качестве α берут число, близкое к единице. Пусть вероятность того, что |m –m^*| <δ, равняется α;

P [| m –m^* | <δ ] = α, (57)

где δ заданная точность; α -достоверность оценки.

Отсюда: P [m^* - δ < m < m^* + δ] = α (58)

Это соотношение следует понимать так : вероятность того, что интервал (m^*-δ , m^*+ δ) заключает в себе(покрывает) неизвестный параметр m, равна α.

Доверительным интервалом I_α(Рисунок 10)называют интервал (m^*- δ, m^* + δ ) , который покрывает неизвестный параметр с заданной надежностью α.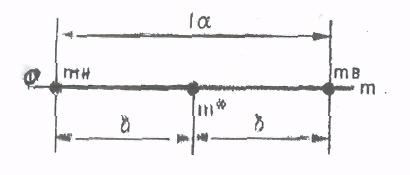



Рисунок 10. Доверительный интервал и доверительные границы.
Из рисунка 10 видно, что I_α = 2δ и характеризует точность оценки.

Интервал имеет случайные концы, которые называют доверительными границами. Доверительные границы сами являются случайными величинами, и зависят от величины выборки.

Доверительные интервалы для оценки математического ожидания нормального распределения могут определяться при известном и неизвестном среднеквадратическом отклонении σ. Если известна величина оценки m^* при известном σ, то верхнюю и нижнюю доверительные границы определяют по следующим уравнениям:

m_н = m^* - t (59)

m_в = m^* + t (60)

где t – число, которое определяется из равенства 2Ф(t) = α.

Из формулы δ = t σ/ следует, что при возрастании объема выборки n число δ убывает и, следовательно, точность оценки увеличивается.

Увеличение надежности оценки α приводит к увеличению t, а следовательно к возрастанию δ, т.е. увеличение надежности α влечет за собой уменьшение ее точности. Минимальный объем выборки, необходимый для оценки математического ожидания с заданной точностью δ и надежностью α находят по формуле:

n = (61)

Когда значение среднего квадратического отклонения неизвестно, вместо величины δ = t определяют величину

δ = t_у (62)

где t _у – табличный коэффициент, определяемый для заданной доверительной вероятности α и числу степеней свободы k = n - 1; S – выборочная характеристика, определяемая по уравнению

S = (63)
Список рекомендуемой литературы

1.Д.Н.Решетов, А.С. Иванов Надежность машины М, Высшая школа, 1988.

2.В.И. Прейсман. Основы надежности техники. Киев «Вица школа», 1979.

3.Ермолов Л.С., Кряжков В.М., Черкун В.Е., - Основы надежности сельскохозяйственной техники. М.: Колос, 1982
Контрольные вопросы:

1.Какие законы распределения наиболее часто используются в теории надежности?

2. Что такое гистограмма и полигон распределения случайной величины?

3. По каким формулам определяются среднее арифметическое и среднее взвешенное?

4. Что такое медиана и мода?

5. Как определяется эмпирическое среднее квадратическое отклонение?

6. На основании какого параметра выдвигается гипотеза о законе распределения?

7. Что такое доверительный интервал и доверительные границы?