Лекции по курсу МС. 4 курс_2010. Лекции по курсу "моделирование систем " Кафедра иу3, 4й курс, 8й семестр. Автор Боевкин Виктор Иванович
 Скачать 306.36 Kb. Скачать 306.36 Kb.
|
1.4. Фильтрующие свойства разложенийВ некоторых приложениях достаточно хорошо известен класс обрабатываемых функций. Например, при экспериментальном определении частотных характеристик входные и выходные сигналы являются гармоническими функциями, или близкие к ним. Отличие от гармонических функций определяется присутствием в экспериментальных данных случайных помех, уровень которых может быть достаточно высоким. Обрабатываемый сигнал f(j) в таких случаях можно представить: f(j) = S0(j) + ah(j); S0(j) = 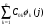 ; j = 1…N (1.21) ; j = 1…N (1.21) Здесь S0(j) – идеальный (незашумленный) сигнал; фk(j), k = 1…n , - известные функции, составляющие идеальный сигнал; h(j) – случайный сигнал с известным законом распределения; а – коэффициент при случайном сигнале, с который условно назовем амплитудой помехи. В качестве базиса для разложения f(j) примем функции фk(j), входящие в идеальный сигнал (21). Целью разложения в этом случае является как можно более точное определение параметров C0k незашумленного сигнала, то – есть фильтрация помех. В результате разложения получим S(j) = 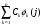 (1.22) (1.22)где коэффициенты разложения Ck вычислены по соотношениям (17) и (20). На Рис. 3 представлено функциональное пространство H (для N = 3), плоскость Sn (для n = 2), а также все величины, входящие в (21) и (22). Вектор aSh(j) является проекцией вектора помехи ah(j) на плоскость Sn, то – есть разложением помехи по базису фk(j). Из треугольника а1а2а3 (рис.3) получим соотношение: aSh(j) + d(j) = ah(j). (1.23) Поскольку вектор ошибки d (отрезок a1a2)ортогонален плоскости Sn , то треугольник a1a2a3 является прямоугольным, поэтому, по аналогу теоремы Пифагора, из уравнения (23) можно получить: a2ESh + Ed = a2Eh (1.24) Здесь a2Eh– энергия помехи ah(j), a2ESh - энергия разложения aSh помехи ah(j), Ed – энергия ошибки разложения d(j) = f(j) – S(j). Фильтрующие свойства разложения можно характеризовать коэффициентом фильтрации Кф, отражающим уменьшение модуля помехи при проектировании ее на базисную гиперплоскость: Кф = 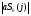 / /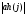 = = 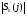 / /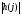 . (1.25) . (1.25)Из прямоугольного треугольника а1а2а3 (Рис.3) и (25) можно получить соотношение: Кф = 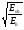 , (1.26) , (1.26)где Eh – энергия случайного сигнала h(j), ESh – энергия разложения Sh(j) этого сигнала. При достаточно больших N эти величины обладают статистической устойчивостью и, согласно [4], их осредненные значения могут быть оценены теоретически. По определению, энергия случайного сигнала h(j) Eh = 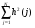 Осредним эту величину по ансамблю реализаций h(j): Eh = M{ 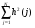 } = } = 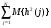 = = 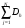 = NDh = N(Gh)2 (1.27) = NDh = N(Gh)2 (1.27)Здесь Dhи Gh - дисперсия и среднеквадратическое отклонение случайной величины h(j) соответственно. При известном (или предполагаемом) законе распределения эти величины известны. Так, для равномерного закона распределения с единичным диапазоном Dh = 1/12 = 0.083; Gh = 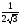 = 0.289 (1.28) = 0.289 (1.28)Разложение случайного сигнала h(j) представим: Sh(j) = 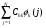 (1.29) (1.29)Энергия этого разложения, согласно (12), имеет вид: Esh = 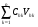 (1.30) (1.30)Величины Chk и Vhk связаны соотношениями (9) и (17). Введем матрицу Q, обратную U из (17), тогда Q = U-1 = 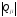 ; j = 1…n , i = 1…n . (1.31) ; j = 1…n , i = 1…n . (1.31)Решение уравнений (9) теперь можно записать: Chk = 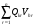 Подставив это в (30), получим: Esh = 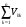 * * 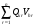 = =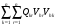 (1.32) (1.32)Осредним (32) по ансамблю реализаций: Esh = M[Esh] = 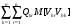 (1.33) (1.33)В соответствии с (20) вычислим M[Vhr Vhk] = M[ 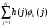 * *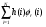 ] = ] == 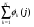 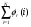 M[h(j)h(i)] (1.34) M[h(j)h(i)] (1.34)Если случайные величины h(j) и h(i) независимы, то M[h(j)h(i)]= 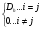 (1.35) (1.35) Подставив (35) в (34) с учетом (20), получим: M[Vhr Vhk] = Dh 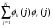 = Dh Urk (1.36) = Dh Urk (1.36)Подставим (36) в (33): Esh = Dh 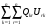 (1.37) (1.37)Внутренняя сумма в (37) является элементом произведения матриц Q и U, которые, согласно (31), взаимно обратны, поэтому 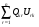 = Qkk Ukk = 1 (1.38) = Qkk Ukk = 1 (1.38)Используя (38) , из (37) получим: Esh = Dhn (1.39) Подставив в выражение (26) для коэффициента фильтрации осредненные значения (27) и (39), получим: Кф = 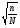 (1.40) (1.40) |
