Лекции по курсу МС. 4 курс_2010. Лекции по курсу "моделирование систем " Кафедра иу3, 4й курс, 8й семестр. Автор Боевкин Виктор Иванович

• Название: Лекции по курсу "моделирование систем " Кафедра иу3, 4й курс, 8й семестр. Автор Боевкин Виктор Иванович
• Анкор: Лекции по курсу МС. 4 курс_2010.docx
• Дата: 01.10.2018
• Размер: 306.36 Kb.
• Имя файла: Лекции по курсу МС. 4 курс_2010.docx
• Тип: Лекции; #25307
• страница: 6 из 7

2.2. Погрешности аналогового моделирования

2.2.1. Особенности аналоговой вычислительной техники

В аналоговых вычислительных машинах (АВМ) каждая переменная величина из решаемой системы дифференциальных уравнений представляется (моделируется) напряжением на соотвтствующем блоке [2.7]. Каждый блок –это решающее устройство, выполняющее свою математическую операцию одновременно с другими блоками, то-есть параллельно во времени. Основой решающего блока является операционный усилитель постоянного тока с большим коэффициентом усиления и глубокой отрицательной обратной связью. Основными решающими блоками являются сумматор и интегратор. Отрицательная обратная связь сумматора осуществляется через активное сопротивление, интегратора – через конденсатор. Стабильность коэффициентов передачи решающих блоков, а вместе с тем и точность выполнения математических операций, зависит от качества используемых сопротивлений и конденсаторов, и не может быть высокой. Изучение влияния погрешностей выполнения операций суммирования и интегрирования на точность решения дифференциальных уравнений рассмотрим на примере уравнения n – ного порядка:
xⁿ + a_n-1x^n-1 + a_n-2x^n-2 +…+ a₁x^ + a₀x = f(t) (2.2.1)

2.2.2. Взаимосвязь приращений корней и коэффициентов характеристического уравнения

Динамические свойства системы, описываемой уравнением (1), в большой степени определяются корнями характеристического уравнения:
P(p,a_k) = pⁿ + a_n-1p^n-1 + a_n-2p^n-2 +…+ a₁p + a₀ = 0 (2.2.2)
При решении уравнения (1) на аналоговой модели погрешности коэффициентов передачи решающих блоков формируют погрешности выставки коэффициентов уравнения (1), а вместе с тем и погрешности в коэффициентах характеристического уравнения (2). Это, в свою очередь, приводит к изменению корней характеристического уравнения, то – есть к изменению динамических свойств моделируемой системы. Для выяснения влияния погрешности выставки параметров аналоговой модели на изменение динамических свойств найдем зависимость малых приращений корней от малых приращений коэффициентов [2.8]. При известных корнях, характеристическое уравнение (2) можно представить ввиде произведения:

P(p,p_j) = (p-p₁)(p-p₂)…(p-p_n) = 0 (2.2.3)
Приравняв коэффициенты при одинаковых степенях p в (2) и (3), получим формулы Виета, выражающие коэффициенты характеристического уравнения через его корни :
a_n-1 = -(p₁+p₂…+p_n)
a_n-2 = (p₁p₂+p₁p₃+…p_n-1p_n) (2.2.4)

……………………………

a₀ = (-1)ⁿp₁p₂…p_n
Обратных прямых выражений корней через коэффициенты в общем случае не существует, однако для малых приращений они могут быть получены. Для этого возьмем полные дифференциалы по параметрам a_k и p_j от выражений (2) и (3) соответственно:

dP(p,a_k) ===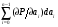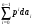

= da₀+pda₁+…+p^n-1 da_n-1 (2.2.5)

dP(p,p_j) =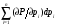= - 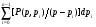(2.2.6)
Для обеспечения равенства полиномов (5) и (6) при любых p
dP(p,a_k) = dP(p,p_j) (2.2.7)
необходимо и достаточно, чтобы оно выполнялось при n различных значений p. В качестве этих значений удобно выбрать p = p_k , k = 1…n. Подставив эти значения в выражение (7) с учетом (5) и (6) получим :
dp_k= - (da₀+da₁ p_k+…+p_k^n-1 da_n-1 )/(p_k-p₁)_…

(p_k-p_k-1)(p_k-p_k+1)…(p_k-p_n), k =1,2,…n. (2.2.8)

Таким образом, по формулам Виета (4) можно выразить коэффициенты характеристического уравнения через его корни, а с помощью соотношений (8) - приращения корней через приращения коэффициентов. Последнее позволяет проверить пригодность АВМ для решения определенной задачи.

2.2.3. Влияние аналогового интегратора на корни характеристического уравнения

Структурная схема аналогового интегратора представлена на рис.1.
Примерные значения параметров схемы [2.9]: коэффициент усиления операционного усилителя К = 10⁸, входное сопротивление R = 1 Мом, емкость конденсатора С = 1мф, сопротивление утечки конденсатора R_k = 10000 Мом. Передаточную функцию W_a(p) схемы можно привести к следующему виду:
W_a(p) = K_a /(p + a) ; K_a = RC = 1сек ; a = 10^-4 1/сек
С учетом инерционных свойств операционного усилителя, передаточную функцию W_a(p) аналогового интегратора примем:

W_a(p) = 1 /(p + a)(1+Tp) ; T = 10^-4 сек (2.2.9)
Структурная схема моделирования уравнения (1) представлена на рис.2.

Напряжения U_k , k = 0…n моделируют производные x^(k) . При идеальных интеграторах с передаточной фикцией
W_и(p) = 1/p (2.2.10)
передаточная функция структурной схемы рис.5.2 имеет вид
W(p) = 1/( pⁿ + a_n-1p^n-1 + a_n-2p^n-2 +…+ a₁p + a₀) , (2.2.11)
что соответствует уравнению (1).

Характеристическое уравнение имеет форму (2), а при известных корнях – форму (3). При наличии в уравнении (3) m вещественных корней и (n-m)/2 комплексных корней, его можно привести к виду:
P(p) = П_к=1^(n-m)/2 (p²+2g_kp+d_k²)П_i=1^m(p+q_i) = 0 (2.2.12)
Определение корней уравнения (12) сводится к приравниванию нулю каждого из сомножителей. Апериодическим составляющим переходного процесса соответствуют сомножители (моды) с вещественными корнями:
(p+q_i) = 0 , p_i = - q_i , i = 1…m (2.2.13)
Колебательным составляющим переходного процесса соответствуют сомножители (моды) с комплексными корнями:
(p²+2g_kp+d_k²) = 0 , p_1k,2k = -g_k,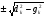

k = 1…(n – m)/2 (2.2.14)
Рассмотрим теперь работу схемы на рис.2. при аналоговых интеграторах с передаточной функцией (9), которую представим в следующем виде:
W_a(p) = 1/D(p), D(p) = (p+a)(Tp+1) (2.2.15)
Здесь D(p) – оператор аналогового интегратора.

Сравнивая передаточные функции идеального (10) и аналогового (15) интеграторов, можно видеть, что передаточную функцию схемы моделирования рис.2.2. при аналоговых интеграторах можно получить, подставив в (11) вместо оператора p из (10) оператор D из (15):
W(p) = 1/( Dⁿ + a_n-1D^n-1 + a_n-2D^n-2 +…+ a₁D + a₀)

(2.2.16)
Характеристическое уравнение (12), соотношения (13) и (14) для аналоговых интеграторов также формируются путем замены p на D. Для вещественных корней, из (13)
(D + q_i) = (p + a )(Tp + 1) + q_i = 0 (2.2.17)
Отсюда, при малых a и T, получим:
p_i1 = - q_i – a = p_i – a ; p_i2 = - 1/T + q_i ; i = 1…m (2.2.18)
Из выражения (18) видно, что каждому вещественному корню р_i характеристического уравнения (2) исходного уравнения соответствуют два корня схемы моделирования (рис.2.2) с аналоговыми интеграторами. Один из них – p_i1 – смещенный на малую величину а корень p_i . Второй, дополнительный, корень p_i2 – располагается вблизи большой по модулю величины – 1/T .

Для комплексных корней (14), используя (15), получим уравнение четвертой степени:
(D²+2g_kD+d_k²) = p⁴ + 2p³T(1+aT) + p² (1+ 4aT+a²T²+2g_kT) + 2p(1+aT)(a+g_k) + (d_k² + 2g_ka + a²) = 0 (2.2.19)
Проектируем приближенное (для малых a и T) решение уравнения (19) ввиде:
(p² + 2g_kp + d_k²)(T²p² + 2Tz_kp +1) = 0 (2.2.20)
Приравняв коэффициенты при одинаковых степенях p в уравнениях (19) и (20), можно получить приближенные соотношения:
g_k ²= g_k² + 2d_ka ; d_k = d_k +(a – g_k²T)

z_k = 1 – T(d_k +a) (2.2.21)
Из выражений (20) и (21) можно видеть, что аналоговые интеграторы приводят к смещению основных комплексных корней (параметры g_k и d_k ) , и к появлению пары дополнительных комплексных корней с вещественной частью, близкой к –1/T и затуханием z_k ,близким к единице.

Итак, применение аналоговых интеграторов для решения дифференциальных уравнений приводит к смещениию корней характеристического уравнения и появлению дополнительных корней.

Мерой пригодности аналоговых интеграторов для решения конкретной задачи является малость смещения основных корней и достаточно большая удаленность дополнительных корней от мнимой оси комплексной плоскости в сторону отрицательных значений. Для определенного типа аналоговой модели (с известными a и T) класс решаемых задач задается ограничениями на корни характеристического уравнения:

1/T>>[Re(p_k)] >>a ; 1/T>>[Im(p_k)] >>a