Лекции по курсу МС. 4 курс_2010. Лекции по курсу "моделирование систем " Кафедра иу3, 4й курс, 8й семестр. Автор Боевкин Виктор Иванович
 Скачать 306.36 Kb. Скачать 306.36 Kb.
|
     Московский Государственный Технический Университет им. Баумана (МГТУ им. Баумана) Факультет Информатика и системы управления Кафедра Информационные системы и коммуникации (ИУ-3) ЛЕКЦИИ по курсу “МОДЕЛИРОВАНИЕ СИСТЕМ ” Кафедра ИУ-3, 4-й курс, 8-й семестр.    Автор: Боевкин Виктор Иванович   Москва 2009 Оглавление Введение Раздел 1. Фильтрация помех при моделировании 1.1 Алгоритм разложения сигнала по неортогональному базису 1.2. О сходимости разложений 1.3. Разложение дискретных функций1.4. Фильтрующие свойства разложений1.5. Оценка уровня помех в обрабатываемой реализации1.6. Оценка погрешностей разложения1.7. Численная оптимизация по параметрам базиса1.8 Оценка погрешностей разложения методом статистического моделированияРаздел 2. Моделирование непрерывных систем 2.1. Цифровое моделирование непрерывных динамических систем2.1.1 Методы цифрового моделирования2.1.2. Численное решение линейных дифференциальных уравнений методом разложения в ряд Тейлора2.1.3. Выражение ошибки численного решения через изменения коэффициентов дифференциального уравнения2.1.4. Выражение ошибки численного решения через изменение корней характеристического уравнения2.1.5. Устойчивость численного решения2.1.6. Повышение точности численного решения методом коррекции уравнений движения2.2. Погрешности аналогового моделирования2.2.1. Особенности аналоговой вычислительной техники2.2.2. Взаимосвязь приращений корней и коэффициентов характеристического уравнения2.2.3. Влияние аналогового интегратора на корни характеристического уравнения2.3. Погрешности полунатурного моделированияУпражненияЛитератураВведение Термин « моделирование » имеет очень широкое применение и означает абстрактное воспроизведение интересующих нас свойств некоторого устройства или процесса с целью их изучения. Необходимо, чтобы «модель» достаточно точно совпадала с объектом именно в изучаемой области свойств. Несовпадение других свойств не имеет значения. Во многих областях техники используются геометрические модели, воспроизводящие в натуральную величину или в масштабе внешний вид и (или) внутреннее устройство архитектурных сооружений, автомобилей, кораблей, самолетов, кинематических схем механизмов и т. д. По таким моделям изучается и корректируется внешний вид, функционирование кинематических схем. При известных критериях подобия по геометрическим моделям изучаются гидро- и аэро-динамические свойства объектов. Наиболее абстрактным является математическое моделирование динамических процессов. В этом случае термины «модель», «математическая модель» применяется к математическому описанию процесса ввиде,например, системы дифференциальных уравнений. Эти же термины относятся и к вычислительной аппаратуре, решающей эти уравнения: некоторый набор аналоговых и (или) цифровых вычислительных машин вместе со структурной схемой их соединений. Важным элементом проектирования сложных динамических систем является полунатурное моделирование. В этом случае одна часть системы представляется математической моделью (например - объект управления), а друга часть представлена реальной аппаратурой (например – аппаратурой автопилота). Необходимыми элементами полунатурного моделирования являются преобразующие устройства, согласующие взаимодействие математической и реальной частей. В особо ответственных случаях применяется параллельное моделирование, когда одновременно с реальным процессом функционирует модель этого процесса, что позволяет выявлять и ликвидировать внештатные и аварийные ситуации. Для определения статистических характеристик сложных систем, находящихся под воздействием случайных воздействий, применяется статистическое моделирование. В этом случае моделирование проводится многократно, при различных реализациях случайных воздействий, что позволяет получить статистические характеристики изучаемой системы. При проведении моделирования главным вопросом является его достоверность, что связано с оценкой погрешностей моделирования и их минимизацией. Проведение экспериментов при моделировании связано с большим количеством измерений. Выбор измерительных приборов и анализ влияния их погрешностей на результаты моделирования – необходимый этап работы. В процессе проведения экспериментов возникают помехи или шумы, чаще всего электрического характера. Оценка уровня помех и их влияния на погрешности моделирования, фильтрация помех с целью минимизации их влияния – также необходимы. При математическом моделировании сложной динамической системы необходимо правильно выбрать математическое описание этой системы. Дело в том, что математическое описание любого реального объекта может быть сколь угодно сложным. Если учитывать, например, распределенные параметры всех узлов объекта, таких, как вращающиеся валы – потребуется описание ввиде систем уравнений в частных производных. Реализация таких моделей с помощью обычных вычислительных средств становится затруднительной или даже невозможной. Слишком простое математическое описание может привести к ошибкам не только количественного, но и качественного характера, например – неправильной оценке факта устойчивости. Таким образом, математическое описание моделируемой системы должно быть адекватным решаемой задаче. При выбранном математическом описании необходимо правильно выбрать вычислительные средства и программы, обеспечивающие достаточно точное решение. Для этого необходимо уметь правильно оценивать погрешности при решении конкретной задачи. При проведении полунатурного моделирования необходимо оценивать и минимизировать погрешности решения, вызванные неидеальностью преобразующих устройств. Раздел 1. Фильтрация помех при моделировании 1.1 Алгоритм разложения сигнала по неортогональному базису При обработке экспериментальных функций времени может возникнуть необходимость представления этих функций в виде аналитических выражений. Непрерывный процесс f(t), определенный на интервале T, можно разложить по заранее выбранной системе базисных функций ф1(t)…фn(t), гдеn – число базисных функций. Разложение S(t) имеет вид: S(t) = 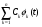 ; f(t) = S(t) + d(t) (1.1) Здесь d(t) = f(t) – S(t) (1.2) ; f(t) = S(t) + d(t) (1.1) Здесь d(t) = f(t) – S(t) (1.2)-ошибка разложения Введем понятие энергии Ey функции (сигнала) y(t): Ey = 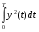 (1.3) (1.3)В качестве критерия, характеризующего удаление S(t) от f(t) на интервале T, то-есть характеризующего качество разложения, примем энергию ошибки Ed = 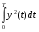 (1.4)При заданных f(t) , T и фi(t) энергия ошибки является функцией от коэффициентов Ci разложения. Коэффициенты разложения будем выбирать из условия минимума энергии ошибки, для чего приравняем нулю частные производные (1.4)При заданных f(t) , T и фi(t) энергия ошибки является функцией от коэффициентов Ci разложения. Коэффициенты разложения будем выбирать из условия минимума энергии ошибки, для чего приравняем нулю частные производные 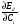 = 0 ; i = 1…n . (1.5) = 0 ; i = 1…n . (1.5)Из (4) и (2) можно получить: Ed = 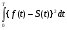 = Ef – A + Es ; (1.6) = Ef – A + Es ; (1.6)Ef = 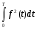 , A = -2 , A = -2 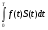 , Es = , Es = 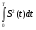 С учетом (6) уравнения (5) станут: 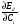 = = 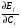 - - 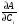 + + 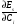 = 0; i = 1…n (1.7) = 0; i = 1…n (1.7)Используя (1) и (6) , выпишем частные производные: 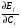 = 0; = 0; 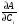 = 2 = 2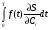 (1.8) (1.8)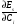 = 2 = 2 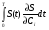 ; ; 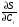 = фi (t) = фi (t)Подставив (8) в (7), получим: 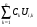 = Vi; i = 1…n . (1.9) = Vi; i = 1…n . (1.9)Здесь введены обозначения: Ui,k = 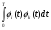 ; Vi = ; Vi = 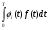 . (1.10) . (1.10)Линейная алгебраическая неоднородная система уравнений (9) вместе с обозначениями (10) определяет значения коэффициентов разложения Ci , при которых энергия Ed ошибки разложения минимальна. Используя обозначения (10), энергию ошибки (4) при произвольных значениях коэффициентов Ci можно представить: Ed = Ef – 2 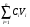 + + 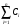 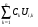 . (1.11) . (1.11)При оптимальных значениях коэффициентов, вычисленных из (9), энергия ошибки (11) имеет вид: Ed = Ef - 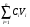 = Ef –Es . (1.12) = Ef –Es . (1.12)Приведенные выше результаты имеют достаточно прозрачное геометрическое представление. Введем в рассмотрение пространство H (бесконечномерное), элементами которого являются функции, определенные на интервале T, и удовлетворяющие условиям Дирихле, то – есть ограниченные и имеющие конечное число экстремумов и разрывов первого рода. Любая такая функция представляется в пространстве H точкой или, что эквивалентно, вектором. Определим скалярное произведение двух векторов в пространстве H следующим образом: 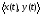 = =  (1.13) (1.13)Пространства, в которых определена операция скалярного произведения, называются Гильбертовыми. Они обладают геометрическими аналогиями, вследствие которых суждения, полученные из геометрического рассмотрения, имеют силу доказательств. Квадрат модуля любого сигнала y(t) в пространстве H равен энергии этого сигнала, что видно из определений энергии (3) и cкалярного произведения (13): 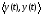 = = 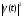 = = 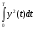 = Ey (1.14) = Ey (1.14)Векторы y(t) и x(t) ортогональны, если их скалярное произведение равно нулю: 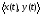 = =  = 0 (1.15) = 0 (1.15)Базисные функции фi(t) изображаются в пространстве H векторами, которые формируют гиперплоскость Sn размерностью n, то есть набор функций фi (t) является неортогональным базисом гиперплоскости Sn. Разложение S из (1) всегда лежит в гиперплоскости Sn а коэффициенты Ci являются координатами S в неортогональном базисе гиперплоскости Sn. Разлагаемая функция f(t), в общем случае, не лежит в гиперплоскости Sn. Ошибка разложения d(t) изображается в пространстве H вектором, соединяющим концы векторов f(t) и S(t). Квадрат длины вектора ошибки, согласно (14), равен энергии ошибки, т.е. принятому критерию близости (4). Из геометрических соображений ясно, что длина 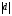 вектора ошибки (а вместе с ней и энергия ошибки) будет минимальной, если вектор ошибки d(t) ортогонален гиперплоскости Sn. Последнее выполняется, когда вектор ошибки d(t) ортогонален ко всем базисным функциям фi(t), формирующим гиперплоскость Sn. Принимая во внимание определение скалярного произведения (13) и условие ортогональности (15), можно записать: вектора ошибки (а вместе с ней и энергия ошибки) будет минимальной, если вектор ошибки d(t) ортогонален гиперплоскости Sn. Последнее выполняется, когда вектор ошибки d(t) ортогонален ко всем базисным функциям фi(t), формирующим гиперплоскость Sn. Принимая во внимание определение скалярного произведения (13) и условие ортогональности (15), можно записать: 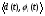 = = 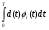 = 0 = 0 Легко видеть, что подставив сюда d(t) = f(t) – S(t) из (2) и используя обозначения (10), получим систему уравнений (9). Величины (10) при этом являются скалярными произведениями: Ui,k = 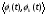 = = 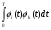 ; (1.16) ; (1.16)Vi = 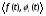 = = 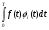 . .Матричная запись системы уравнений (9) имеет вид: U*C = V (1.17) Здесь U – квадратная матрица размерностью n*n с элементами Ui,k , V – вектор правых частей размерностью n*1 с элементами Vi , C– вектор неизвестных размерностью n*1 с элементами Ck.. |
