Лекции по курсу МС. 4 курс_2010. Лекции по курсу "моделирование систем " Кафедра иу3, 4й курс, 8й семестр. Автор Боевкин Виктор Иванович

• Название: Лекции по курсу "моделирование систем " Кафедра иу3, 4й курс, 8й семестр. Автор Боевкин Виктор Иванович
• Анкор: Лекции по курсу МС. 4 курс_2010.docx
• Дата: 01.10.2018
• Размер: 306.36 Kb.
• Имя файла: Лекции по курсу МС. 4 курс_2010.docx
• Тип: Лекции; #25307
• страница: 5 из 7

1.8 Оценка погрешностей разложения методом статистического моделирования

Погрешности оценок (55) параметров q_0i и C_0k незашумленного сигнала S₀(j) (50) можно произвести с помощью статистического моделирования. Задав значения параметров q_0i и C_0k и амплитуду шума а, сформируем ансамбль зашумленных реализаций, отличающихся одна от другой реализациями шума h(j). Разложение каждой реализации из ансамбля даст свою оценку (55) параметров q_0i и C_0k , что позволяет вычислить погрешности всех параметров для данной реализации:

dq_i = q_0i – q_i ^опт, i = 1…m, dC_k = C_0k – C_k^опт, k = 1..n (1.56)

Разложение ансамбля зашумленных реализаций позволяет сформировать статистики ошибок по всем параметрам, откуда можно получить оценки законов распределения ошибок и их моменты для заданной амплитуды помехи. При обработке единичной (уникальной) экспериментальной реализации амплитуда помехи определяется по (41), а статистическое моделирование, упомянутое выше, производится вокруг разложения S(j) этой экспериментальной реализации. Это позволяет получить статистические характеристики погрешностей параметров сигнала, представленного единичной реализацией.

Раздел 2. Моделирование непрерывных систем

2.1. Цифровое моделирование непрерывных динамических систем

2.1.1 Методы цифрового моделирования

При решении дифференциальных уравнений на ЦВМ каждая переменная представляется отсчетами, задаваемыми или вычисляемыми в дискретные моменты времени [2.1]. Значения отсчетов также имеют дискретную структуру, определяемую конечностью разрядной сетки машины.

Отсчеты различных переменных появляются на входных и выходных регистрах машины в определенной последовательности, задаваемой программой.

В универсальных ЦВМ все математические операции производятся последовательно в одном арифметическом устройстве, поэтому время решения задачи зависит от ее сложности. За счет увеличения времени решения можно практически неограниченно повышать точность решения. В некоторых случаях определяющее значение имеет возможность решения задачи в реальном масштабе времени.

Для получения значений всех переменных в момент времени

t_m+1 = t_m + h, где h – шаг дискретизации, необходимо провести ряд математических операций над значениями переменных в предыдущие моменты времени, на что затрачивается машинное время dt. Для решения задачи в реальном масштабе времени необходимо, чтобы dt < h . Выполнение этого условия заставляет искать компромисс между скоростью и точностью решения с учетом, разумеется, допустимых для данной задачи погрешностей.

Рассмотрим подробнее погрешности, возникающие при численном решении на ЦВМ системы дифференциальных уравнений с заданными начальными условиями .

Погрешности решения определяются двумя факторами: дискретизацией переменных по величине и по времени [2.2]. Ошибки первого типа обычно называют ошибками округления, а второго - ошибками дискретизации по времени, ошибками усечения (имеется в виду усечение ряда Тейлора).

Ошибки округления зависят от разрядной сетки машины, способа округления чисел и количества вычислительных операций. В частности, с ростом количества временных шагов решения ошибки округления могут накапливаться. Ошибки дискретизации связаны с пошаговым численным решением системы дифференциальных уравнений. В машине тем или иным способом генерируется последовательность временных точек t_m с шагом h. В каждой точке t_m точное решение x(t_m) аппроксимируется величинами x(t_m), которые вычисляется по предыдущим значениям.

Ошибки численных решений подразделяют на локальные и глобальные. Под локальными понимает ошибки, возникающие в процессе вычислений на одном временном шаге, считая что предыдущие значения известны точно.

Глобальная ошибка - отличие точного решения (обычно неизвестного) от вычисленного на произвольном шаге интегрирования.

Численные методы решения дифференциальных уравнений принято делить на одношаговые и многошаговые. В одношаговых методах для вычисления решения в точке t_m+1 необходимо знать решение только в точке t_m , и задача Коши решается с первого же шага. В многошаговых методах для вычисления решения в точке t_m+1 необходимо знать значения переменных в нескольких предыдущих точках.

2.1.2. Численное решение линейных дифференциальных уравнений методом разложения в ряд Тейлора

Рассмотрим матричное однородное линейное дифференциальное уравнение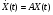

(2.1.1)
Одним из методов численного решения дифференциальных уравнений является разложение решения на шаге h в ряд Тейлора [2.4] относительно предыдущего момента времени t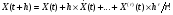
(2.1.2)
Значения входящих в ряд Тейлора производных определим из уравнения (1):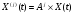

, j = 1…r
Подставив эти значения в (2), получим:
X(t+h) = [I+Ah+A²h²/2…(Ah)^r/r! …]X(t) (2.1.3)

e^Ah = [I+Ah+A²h²/2(Ah)^r/r! …]
Матричный ряд в квадратной скобке представляет собой матричнуюэкспоненту:
(2.1.4)
Таким образом, точное решение уравнения (1) на шаге можно представить в виде:

X(t+h) = e^AhX(t) (2.1.5)
При численном решении ряды в соотношениях (2), (3) и (4) усекаются. Порядком r метода численного решения называется максимальная степень шага h , оставляемая в разложении. Представим матричный экспоненциальный ряд в виде суммы:
e^Ah = e^Ah + de^Ah , e^Ah = I+Ah+A²h²…(Ah)^r/r! ,

(2.1.6)

de^Ah = (Ah)^r+1/(r+1)! +…
где e^Ah - усеченная экспонента, de^Ah - отбрасываемая часть экспоненциального ряда (4).

Результат X(t+h) приближенного численного решения уравнения (1) на шаге h методом r -го порядка можно представить в следующем виде:
X(t+h) = [I+Ah+A²h²…(Ah)^r/r!]X(t) = e^AhX(t) (2.1.7)
Умножая матрицы (6) справа на X(t) с учетом (7), получим
X(t+h) = e^AhX(t) = e^AhX(t) + de^AhX(t) = X(t+h) + dX(t+h) ,

(2.1.8)
где ошибка численного решения на шаге h или локальная ошибка метода

r -того порядка равна:
dX(t+h) = de^AhX(t) = [(Ah)^r+1/(r+1)! +…]X(t) (2.1.9)
Для приближенной оценки локальной ошибки можно использовать соотношение

dX(t+h)[ (Ah)^r+1/(r+1)! ]X(t)

2.1.3. Выражение ошибки численного решения через изменения коэффициентов дифференциального уравнения

Сравнивая точное решение (5) с приближенным численным решением (7) можно видеть, что процедура вычисления на шаге h для них одинакова: предыдущее значение X(t) умножается слева на некоторую матрицу. Однако в точном решении X(t) умножается на матрицу полной экспоненты e^Ah , а в приближенном - на матрицу усеченной экспоненты е^Ah.

Зададимся вопросом: для какого, измененного по отношению к (1), уравнения приближенное численное решение X(t+h) из(7) является точным?

Измененное уравнение (1) запишем следующим образом: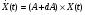
(2.1.10)

Его точное решение на шаге h
X(t+h) = e^(A+dA)hX(t) (2.1.11)
Приравняв выражения (2) и (11), можно получить :

e^(A+dA)h = e^Ah (2.1.12)
Это уравнение определяет матрицу dA из уравнения (10).

Матричную экспоненту (12) представим в виде:
e^(A+dA)h = e^Ahe^dAh
Отсюда и из (6) можно получить:
e^dAh – I = - e^-Ah de^Ah (2.1.13)
Представив матрицы в виде степенных разложений и оставляя только главные члены, получим приближенное соотношение :

dAh- (Ah)^r+1 /(r+1)! (2.1.14)
Соотношения (13) и (14) позволяют вычислить матрицу dA, входящую в измененное уравнение (10). Точное решение этого уравнения совпадает с приближенным численным решением уравнения (1) методом r-того порядка. Таким образом, матрицу dA можно использовать в качестве характеристики погрешностей численного решения через изменение коэффициентов дифференциального уравнения (1).

Используя (14) можно выразить локальную ошибку численного решения (9) через dA:
dX(t+h) = - dAhX(t)
Если по условиям решаемой задачи можно сформулировать допустимые изменения коэффициентов dA, то соотношения (13) и (14) позволят осуществить предварительный выбор порядка метода r и шага дискретизации h.

2.1.4. Выражение ошибки численного решения через изменение корней характеристического уравнения

Приведем матрицу A к диагональному виду [2.6]:

A = S L S^-1 (2.1.15)
Здесь L –диагональная матрица, составленная из собственных значений Z_k матрицы А, являющихся корнями характеристического уравнения
det(IZ – A ) = 0 , (2.1.16)
S - диагонализирующая матрица, составленная из собственных векторов матрицы А.

Известно, что диагонализирующая матрица S сохраняет свой вид для любой степени А и для любого матричного полинома по степеням А, включая сходящиеся степенные ряды. Диагонализируя матричную экспоненту (4) и умножая ее слева на S^-1 и справа на S, получим:
e^Lh = I + Lh + (Lh)²/2 + …+ (Lh)^r/r! + (Lh)^r+1 /(r+1)! +…

(2.1.17)
Здесь e^Lh – диагональная матрица со скалярными экспонентами

e^Zkh по диагонали.

Диагонализируя соотношения (6) и умножая их слева на S^-1 и справа на S, получим:

e^Lh = e^Lh + de^Lh , e^Lh = I+Lh+L²h²…(Lh)^r/r! ,

(2.1.18)

de^Lh = (Lh)^r+1)/(r+1)! + …

Все матрицы в (18) диагональные.

Диагонализируем соотношение (12):
e^(L+dL)h = e^Lh (2.1.19)

Напомним, что матрица dA в (12) характеризует ошибку численного решения в области коэффициентов решаемого уравнения (1).

Аналогично, диагональная матрица dL из (19) характеризует ошибку численного решения в области корней характеристического уравнения (16). Точное решение (19) относительно dL имеет вид:
dL = ln(e^Lh )/h – L (2.1.20)

Диагонализируя (13), получим другю форму точного решения (19):
e^dLh – I = - e^-Lh de^Lh (2.1.21)
В (20) и (21) все матрицы диагональные, поэтому эти соотношения верны для любой строки, то-есть для любого корня характеристического уравнения (16). Учитывая вышесказанное и разлагая входящие в (21) экспоненты в степенные ряды, можно получить приближенные скалярные выражения разной степени точности:

dZ_k h- (Z_kh)^r+1 [1 – Z_kh(r+1)/(r+2) +…]/(r+1) dZ_k h- (Z_kh)^r+1 /(r+1)! (2.1.22)
Как видно из выражений (20) - (22), смещение dZ_k зависит только от

k -того корня Z_k и не зависит от других корней характеристического уравнения.

Таким образом, численное решение системы дифференциальных уравнений (1) с корнями характеристического уравнения

Z₁ , ..., Z_n эквивалентно точному решению другой системы уравнений со смещенными корнями Z_k + dZ_k , k = 1,…n, где смещения корней определяется соотношениями (2.1.20)…(2.1.22).

Если по условиям решаемой задачи можно сформулировать

допустимые изменения корней dZ_k характеристического уравнения, то соотношения (2.1.20) …(2.1.22) позволят осуществить предварительный выбор порядка метода r и шага дискретизации h.

2.1.5. Устойчивость численного решения

Выше было показано, что численное решение системы дифференциальных уравнений (1) с матрицей L собственных значений эквивалентно точному решению системы уравнений со смещенной матрицей собственных значений L+dL, определяемой выражением (19). Так как входящие в него матрицы диагональны, то легко написать соответствующие скалярные соотношения:
e^Zkh = e^(Zk+dZk)h = e^bkh , b_k = Z_k+dZ_k , k=1…n (2.1.23)
где b_k – смещенные собственные значения.

Устойчивость исходной системы уравнений (1) или, что то же самое, ее точного решения, определяется следующими условиями:
Re(Z_k) < 0 , k = 1…n.
При численном решении дифференциального уравнения корни смещаются на dZ_k . Это может привести к тому, что какой-то смещенный корень b_k переместится в правую полуплоскость, что будет соответствовать неустойчивости численного решения.

Условием устойчивости численного решения является, очевидно, соотношение:

Re(b_kh) = Re[(Z_k +dZ_k)h] < 0 , k=1…n. (2.1.24)
Из (23) с учетом (18) найдем значение смещенного корня:
b_kh = ln(e^Zkh) = ln[1+Z_kh+…+(Z_kh)^r/r!] (2.1.25)
Представим e^Zkh в виде комплексного числа:
e^Zkh = u + iv = Ne^iф , (2.1.26)

N =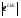=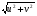, ф= arctg(v/u)
Учитывая (25) и (26) , условия устойчивости численного решения (24) можно записать:
Re(b_k ) = ln 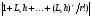< 0 (2.1.27)
В координатах u и v из (26) областью устойчивости является круг единичного радиуса с центром в начале координат:
u² + v² < 1 (2.1.28)
Соотношения (27) и (28) позволяют избежать грубых ошибок при выборе шага дискретизации h и порядка

метода r.

2.1.6. Повышение точности численного решения методом коррекции уравнений движения

Приближенное численное решение X(t+h) = e^Ah X(t) дифференциального уравнения (1) эквивалентно точному решению Х(t+h) = e^(A+dA)h X(t) измененного уравнения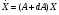
,
где dA определяется из соотношения
e^Ah = e^(A+dA)h
Это позволяет поставить задачу о предварительной коррекции исходного уравнения таким образом, чтобы численное решение скорректированного уравнения стало равным точному решению исходного уравнения. Исходное уравнение (1) имеет точное решение на шаге:

X(t+h) = e^Ah X(t) (2.1.29)
Введем скорректированное уравнение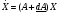
(2.1.30)
Численное решение уравнения (30) на шаге можно записать так:
X(t+h) = e^(A+dA)h X(t) (2.1.31)
Здесь

e^(A+dA)h = [I + (A+dA)h + …(A+dA)^rh^r /r! ] (2.1.32)
- усеченная экспонента матрицы (A+dA) .

Приравнивая решения (29) и (31), можно получить соотношения:
e^Ah = e^(A+dA)h ; e^(A+dA)h – e^Ah = de^Ah (2.1.33)
Отсюда, используя соотношения (6) и (32)и пренебрегая старшими степенями dA , получим :
dAh [I + Ah + …+ (Ah)^(r-1) /(r-1)! ] = de^Ah (2.1.34)
В первом приближении оценку dA получим из (5.34) с учетом (6):
dAh(Ah)^(r+1) /(r+1)! ( 2.1.35)
Сравнивая (35) с (14) можно видеть, что в первом приближении
dA-dA
Уравнения (5.33)…(5.35) с разной степенью точности определяют корректирующую матрицу dA , которую нужно прибавить к матрице исходного уравнения (5.1), чтобы численное решение скорректированного уравнения (5.30) совпало с точным решением на шаге исходного уравнения (1). Диагонализируя соотношения (33)…(35), получим:
e^Lh = e^(L+dL)h ; e^(L+dL)h – e^Lh = de^Lh
dLh [I + Lh + …+ (Lh)^(r-1) /(r-1)! ] = de^Lh (2.1.36)
dLh = (Lh)^(r+1) /(r+1)!
Все выражения в (36) являются диагональными матрицами, поэтому могут быть переписаны в скалярном виде:
e^Zkh = e^(Zk+dZk)h ; e^(Zk+dZk)h – e^Zkh = de^Zkh
dZ_kh [I + Z_kh + …+ (Z_kh)^(r-1) /(r-1)! ] = de^Zkh (2.1.37)
dZ_kh = (Z_kh)^(r+1) /(r+1)! k= 1…n
Уравнения (37) с разной степенью точности определяют

приращения dZ_k , на которые нужно скорректировать

собственные значений Z_k матрицы А, чтобы численное решение измененного таким образом уравнения совпало с точным решением на шаге исходного уравнения (1).

Приведенные в разделе 2.1 результаты получены для решения линейных однородных дифференциальных уравнений методом разложения в ряд Тейлора. Однако, во многоих случаях, полученные оценки могут быть распростронены на:

- неоднородные уравнения [2.5]

- линеаризуемые уравнения

- другие одношаговые методы решения дифференциальных уравнений, основанные на приближении локальной ошибки к ошибке разложения в ряд Тейлора.