Лекции по курсу МС. 4 курс_2010. Лекции по курсу "моделирование систем " Кафедра иу3, 4й курс, 8й семестр. Автор Боевкин Виктор Иванович
 Скачать 306.36 Kb. Скачать 306.36 Kb.
|
2.3. Погрешности полунатурного моделированияПри полунатурном моделировании система управления замыкается через преобразующее устройство ,как показано на рис .2.3, где обозначено: Wo(p) – передаточная функция разомкнутой системы управления (вместе с объектом управления), Wp(p) – передаточная функция преобразующего устройства [Л5.1].? Пусть Wo(p) = B(p)/A(p), Wp(p) = (1+G(p))/(1+Q(p)) B(p) = 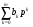 , A(p) = , A(p) =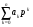 , an = 1 (2.3.1) , an = 1 (2.3.1) G(p) = 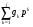 , Q(p) = , Q(p) =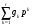 , ,При идеальном преобразующем устройстве , когда Wp(p) = 1, передаточная функция замкнутой системы имеет вид: WI(p) = B(p)/[A(p) + B(p)] , а характеристическое уравнение RI(p) = A(p) +B(p) =0 . (2.3.2) Корни характеристического уравнения (23) будем считать известными и обозначим pI1 , pI2 , …pIn (2.3.3) Характеристическое уравнение передаточной функции преобразующего устройства, и его корни, в соответствии с (22), запишем: Rp(p) = 1 + Q(p) = 0 , pp1 , pp2…ppr (2.3.4) Коэффициенты полинома Q(p) будем считать малыми, так, что модули корней (25) много больше модулей корней (24).В пределе, при Q(p) => 0, limQ=>0 [pIj] = 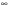 Передаточная функция замкнутой системы (см.рис. 2.3.) с учетом преобразующего устройства и ее характеристическое уравнение имеют вид: W(p) = B(p)(1 + Q(p))/[A(p)(1+Q(p))+B(p)(1+G(p))] R(p) = [A(p)(1+Q(p))+B(p)(1+G(p))] = 0 (2.3.5) Характеристическое уравнение (5) имеет n + r корней: p1 , p2 …pn ,pn+1 …pn+r Представляется очевидным, что при Q(p) 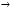 0 и G(p) 0 и G(p)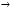 0 первые n корней уравнения (5) стремятся к корням уравнения (2), а последние r корней стремятся в бесконечность по отрицательной полуоси, как и корни уравнения (4). 0 первые n корней уравнения (5) стремятся к корням уравнения (2), а последние r корней стремятся в бесконечность по отрицательной полуоси, как и корни уравнения (4).Это позволяет предположить, что характеристический полином R(p) (5) при малых Q(p) и G(p) незначительно отличается от произведения: R1(p) = RI(p)Rp(p) (2.3.6) Введем мало измененные полиномы R, входящие в (6): RI(p) = RI(p) + d RI(p), Rp(p) = Rp(p) + d Rp(p), (2.3.7) R1(p) = RI(p)Rp(p), dRI(p) = dA(p) + dB(p), dRp(p) = dQ(p) Здесь dA(p) = 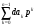 , dB(p) = , dB(p) =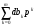 , , dQ(p) = 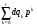 . (2.3.8) . (2.3.8)Величины dak …dqk являются малыми приращениями соответствующих коэффициентов. Приравняем теперь характеристический полином (5) измененному полиному (6): R(p) = RI(p) , (2.3.9) Подставив сюда выражения (7) для приращений полиномов, сокращая одинаковые слагаемые и пренебрегая произведениями малых приращений, получим: dA +dB + QdB + AdQ +BdQ = - B(Q – G) (2.3.10) Левая и правая части этого уравнения являются полиномами по p с наибольшей степенью pn+r . Для выполнения равенства (10) при любых p нужно приравнять коэффициенты при одинаковых степенях p в левой и правой частях уравнения, что даст n+r соотношений между приращениями dak , dbk , dqk . Количество этих приращений, в соответствии с выражениями (8), равно n+r+m+1. Следовательно, для выполнения равенства (10) можно задать произвольно m+1 приращение, что позволяет принять dB = 0. Тогда соотношение (10) приобретет следующий вид: (1 + Q)dA + (A + B)dQ = - B(Q – G) (2.3.11) Система алгебраических уравнений , эквивалентная полиномиальному уравнению (11), - линейная и, в общем случае, неоднородная. Однако, при выполнении условий Q(p) = G(p) , (2.3.12) она станет однородной, т.е. будет иметь тривиальное нулевое решение dA(p) = 0, dQ(p) = 0. Этот результат становится очевидным, если вспомнить, что при выполнении условий (12) передаточная функция преобразующего устройства Wp(p) = 1, что видно из (1). Другой способ решения уравнения (11) исходит из того, что для обеспечения равенства двух полиномов степени (n+r) достаточно обеспечить их равенство в (n+r) точках по аргументу p. Для p , равных корням (3) уравнения(2), соотношение (11) приобретает вид: dA(pIj)(1 + Q(pIj)) = -B(pIj)(Q(pIj) – G(pIj)); j = 1…n (2.3.13) С учетом обозначений (7), систему уравнений (13) можно записать: da0 + da1pIj +…dan-1pIjn-1 = (2.3.14) = -{ B(pIj)(Q(pIj) – G(pIj))}/ (1 + Q(pIj)); j = 1…n Решение системы уравнений (14) дает приращения коэффициентов полинома A(p) и , в силу соотношения dB = 0, приращения коэффициентов полинома RI(p) = 0 (2). Зная приращения коэффициентов полинома (2), можно вычислить приращения его корней по соотношениям (2.2.8). Сравнивая (2.2.8) с (14) можно видеть, что в них входят одинаковые комбинации приращений коэффициентов, поэтому не нужно решать (14) относительно dak , а можно сразу вычислять приращения основных корней системы по формуле dpIj = {B(pIj)(Q(pIj) – G(pIj))}/ (1 + Q(pIj))(pIj - pI1)* *(pIj - pI2)… (pIj - pIn) , j = 1…n (2.3.15) Подставив в (11) корни (4), получим: dQ(ppj)[A(ppj) + B(ppj)] = -B(ppj)(Q(ppj) – G(ppj)); j = 1…r (2.3.16) Проведя аналогичные предыдущим рассуждения и выкладки, получим приращения остальных корней: dppj = B(ppj)(Q(ppj) – G(ppj))/ [A(ppj) + B(ppj)]* *(ppj – pp1) … (pIj - pIn); j = 1…r (2.3.17) Итак, включение в моделирующий комплекс динамического преобразующего устройства приводит к тому, что характеристическое уравнение модели имеет две группы корней: основные - мало измененные корни уравнений идеальной системы, и дополнительные - мало измененные корни характеристического уравнения преобразующего устройства. Задавая допустимое смещение основных корней, а также допустимое сближение основной и дополнительной групп, можно предъявить требования к быстродействию преобразующего устройства. УпражненияКолебательное звено без затухания описывается дифференциальным уравнением: 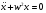 (3.1) (3.1) При идеальном выполнении математических операций такое звено совершает незатухающие гармонические колебания с частотой w. Использование вычислительной техники для моделирования такого звена может привести к затухающим или раскачивающимся колебаниям с измененной частотой. Изменение частоты и декремент затухания (раскачки) при моделировании могут являться мерой погрешности выполнения математических операций. Определить теоретически погрешность по частоте и декремент затухания (раскачки) в зависимости от шага интегрирования для первых четырех порядков метода рядов Тейлора. Решить уравнение (3.1) методами Рунге – Кутта первых четырех порядков. Определить фактическую частоту и декремент затухания (раскачки), сравнить с результатами п.1). Произвести предварительную коррекцию уравнения (3.1), определить теоретические значения частоты и затухания (раскачки). Решить скорректированное уравнение (3.1) методами Рунге – Кутта первых четырех порядков, сравнить с результатами п.3). Вычислить смещение корней уравнения (3.1) при аналоговом моделировании с передаточной функцией интегратора (2.2.15). Найти границу по моделируемой частоте w , отделяющую затухание от раскачки. Промоделировать уравнение (3.1) на аналоговой модели, сравить с результатами п.5). Включить в схему моделирования уравнения (3.1) преобразующее устройство с передаточной функцией W(p) = 1/(1+Tp) Вычислить изменение частоты и декремент раскачки. Предъявить требования к допустимому значению T в зависимости от w. ЛитератураЛ5.1. Боевкин В.И. Оценка точности математического моделирования динамических систем. – М.: Изд. МГТУ, 1990. – 54 с. Л5.2. Калиткин Н.Н. Численные методы. – М.: Наука, 1978. – 512 с. Л5.3. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений. - М .: Мир, 1980. – 279 с. Л5.4. Беки Дж., Карплюс У. Теория и применение гибридных вычислительных систем. – М.: Мир, 1970. – 483 с. Л5.5 Боевкин В.И., Багдамян О. Н. Оценка точности решения задачи Коши по смещению корней характеристического уравнения. – Труды №474. – М.: МВТУ, 1987. – 82 с. Л5.6 Стренг Г. Линейная алгебра и ее применения. – М. : Мир, 1980. - 454 с. Л5.7. Анисимов В.В., Голубкин В. Н. Аналоговые вычислительные машины. – М.: Высш. школа, 1971. – 447 с. Л5.8. Боевкин В.И., Айнутдинова И. Н., Кучминская А.И. Чувствительность динамических свойств линейной системы к изменению ее параметров. – Труды № 284 . – М.: МВТУ, 1979. – 170 с. Л5.9. Боевкин В.И. Моделирование при испытаниях автоматических информационных устройств. – М.: МВТУ, 1985. – 72 с. |
