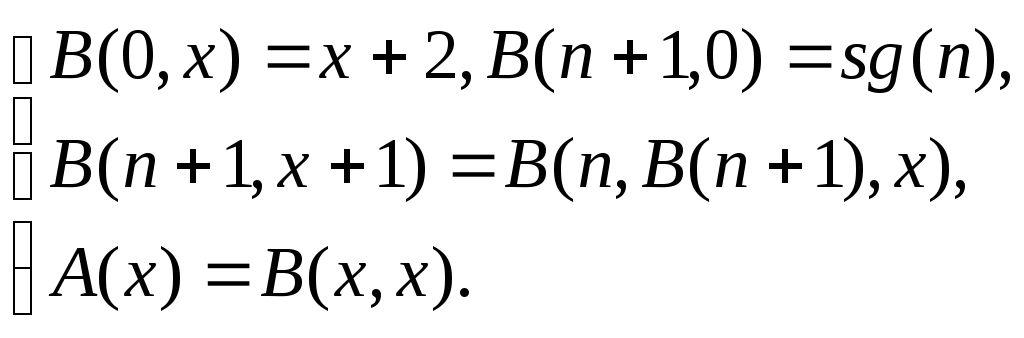Лекции по теории алгоритмов. Лекция Интуитивное представление об алгоритме Интуитивное определение алгоритма. Примеры алгоритмов

• Название: Лекция Интуитивное представление об алгоритме Интуитивное определение алгоритма. Примеры алгоритмов
• Анкор: Лекции по теории алгоритмов
• Дата: 05.05.2022
• Размер: 2.84 Mb.
• Имя файла: Лекции по теории алгоритмов.doc
• Тип: Лекция; #513398
• страница: 4 из 7

Лекция № 4. Рекурсивные функции
1. Примитивно-рекурсивные функции

2. Частично-рекурсивные и общерекурсивные функции
1. Примитивно-рекурсивные функции

С.К.Клини

Формализация понятия алгоритма в терминах рекурсивных функций предложена в 1936 году в работах А.Черча (общерекурсивные функции) и работах С.К.Клини (частично рекурсивные функции, 1938).

А.Черч

Функция непосредственно следующее натуральное число, обозначаемая штрихом, позволяет по числу 0 построить любой начальный отрезок множества натуральных чисел. Обозначения при этом таковы: 0, 0^/=1, 0^//=1^/,=2, …

Функции выбора аргумента определяются равенствами:

W_k(x₁,x₂, x_k,…, x_n)=x_k (1kn).

Функция непосредственно следующее натуральное число, и функции выбора аргумента образуюттак называемое множество базисных функций. Функции, входящие в это множество всюду определены на множестве натуральных чисел.

Говорят, что функция может быть построена при применении оператора суперпозиции к функциям нескольких переменных, если она может быть определена в результате следующих действий:

1) подстановки функции в функцию;

2) переименовывания переменных;

3) отождествления переменных;

4) исключения переменных замещением их константами.

Пример 4.1.1. Даны функции g(y₁,y₂), w(x₁, x₂, x₃). Говорят, что функция f(x₁, y₁, y₂, x₃)=w(x₁, g(y₁,y₂), x₃) построена путем подстановки функции g(y₁,y₂) в функцию w(x₁, x₂, x₃).

Пример 4.1.2. Даны функции g(t), w(x₁, x₂, x₃). Говорят, что функция f(x₁,t,x₃)=w(x₁, g(t), x₃) построена путем переименовывания переменных.

Пример 4.1.3. Даны функции g₁(t), g₂(t), w(x₁, x₂, x₃). Говорят, что функция f(x₁,t)=w(x₁, g₁(t), g₂(t)) построена путем отождествления переменных.

Пример 4.1.4. Дана функция w(x₁, x₂, x₃). Говорят, что функция f(x₁,x₃)= w(x₁, m, x₃) построена путем исключения переменных замещением их константами.

Оператор примитивной рекурсии применяется к двум функциям n-1 и n+1 переменных для построения функции n переменных.

Определяющие соотношения оператора примитивной рекурсии записываются так.

1. При n=1 по натуральному числу m и функции двух переменных h(u,v) строится функция одной переменной f(y):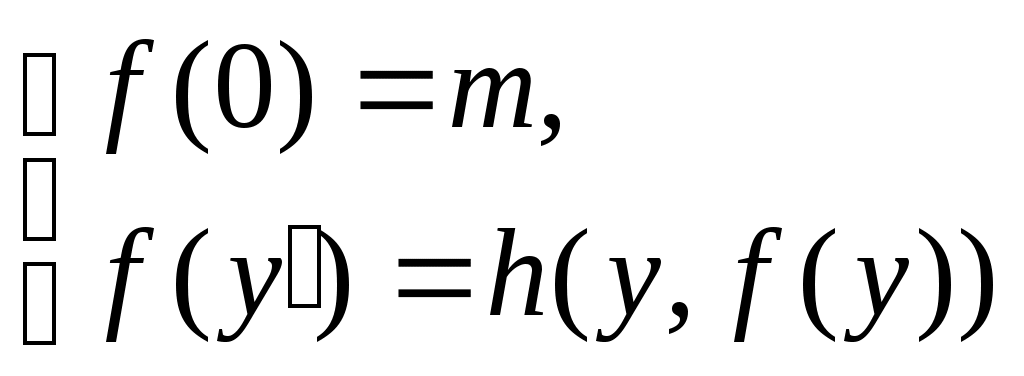

.

2. При n>1 по заданным функциям q(x₁, x₂, …, x_n-1) и h(x₁, x₂, …, x_n+1) строитсяфункцияnпеременных f(x₁, x₂, , x_n–1, x_n):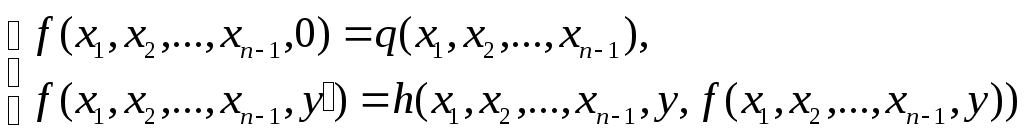

.

Определение 4.1.1. Функция называется примитивно рекурсивной, если она есть базисная функция или может быть построена исходя из базисных функций конечным числом применений операторов суперпозиции и примитивной рекурсии.

Пример 4.1.5. Функция g(x)=x – базисная. Функция h(x₁, x₂, x₃)=x₃ ^/может быть получена применением оператора суперпозиции двух базисных функций x₃ ^/ и w(x₁, x₂, x₃)=x₃. Исходяиз функций g(x)=x, h(x₁, x₂, x₃) построим функцию двух переменных f(x,y) с применением оператора примитивной рекурсии: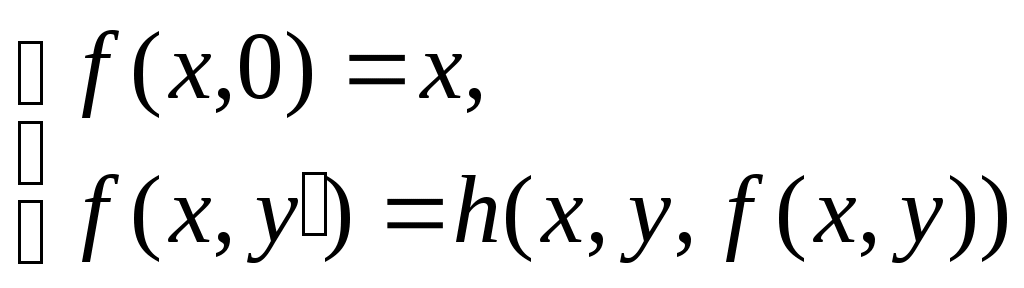



Таким образом, согласно определению эта функция является примитивно рекурсивной. В то же время, исходя из определения функции h(x₁,x₂,x₃) запись функции f(x,y) можно сделать более наглядной:



Или совсем простой – f(x,y)=x+y.

Последнее утверждение проверяется просто:

f(x,0)=x+0=x, f(x,y+1)=x+(y+1)=(x+y)+1= f(x,y)+1=(f(x,y))^/.

Фактически в примере 5 мы доказали примитивную рекурсивность функции f(x,y)=x+y.

Аналогично доказывается примитивная рекурсивность функций: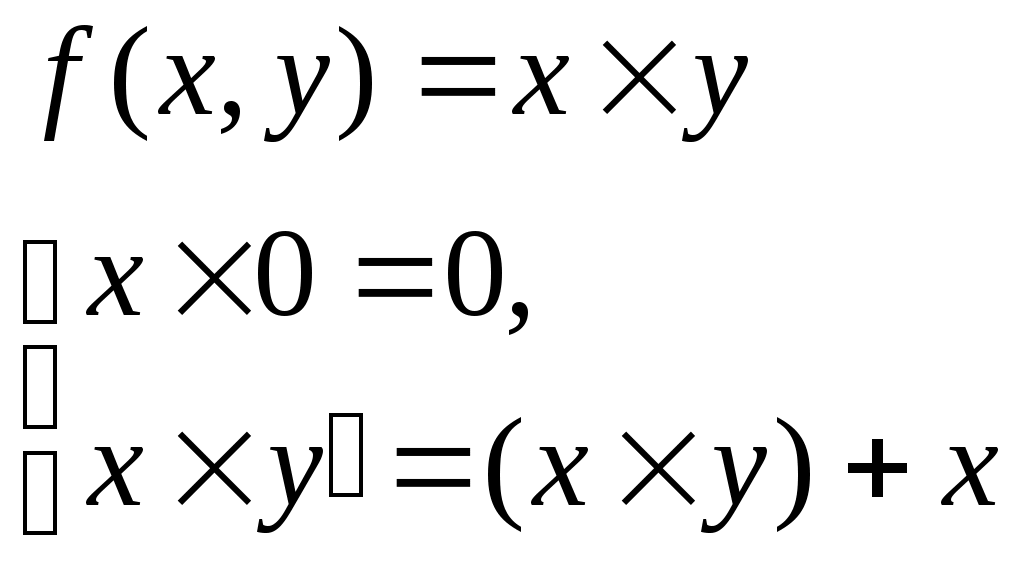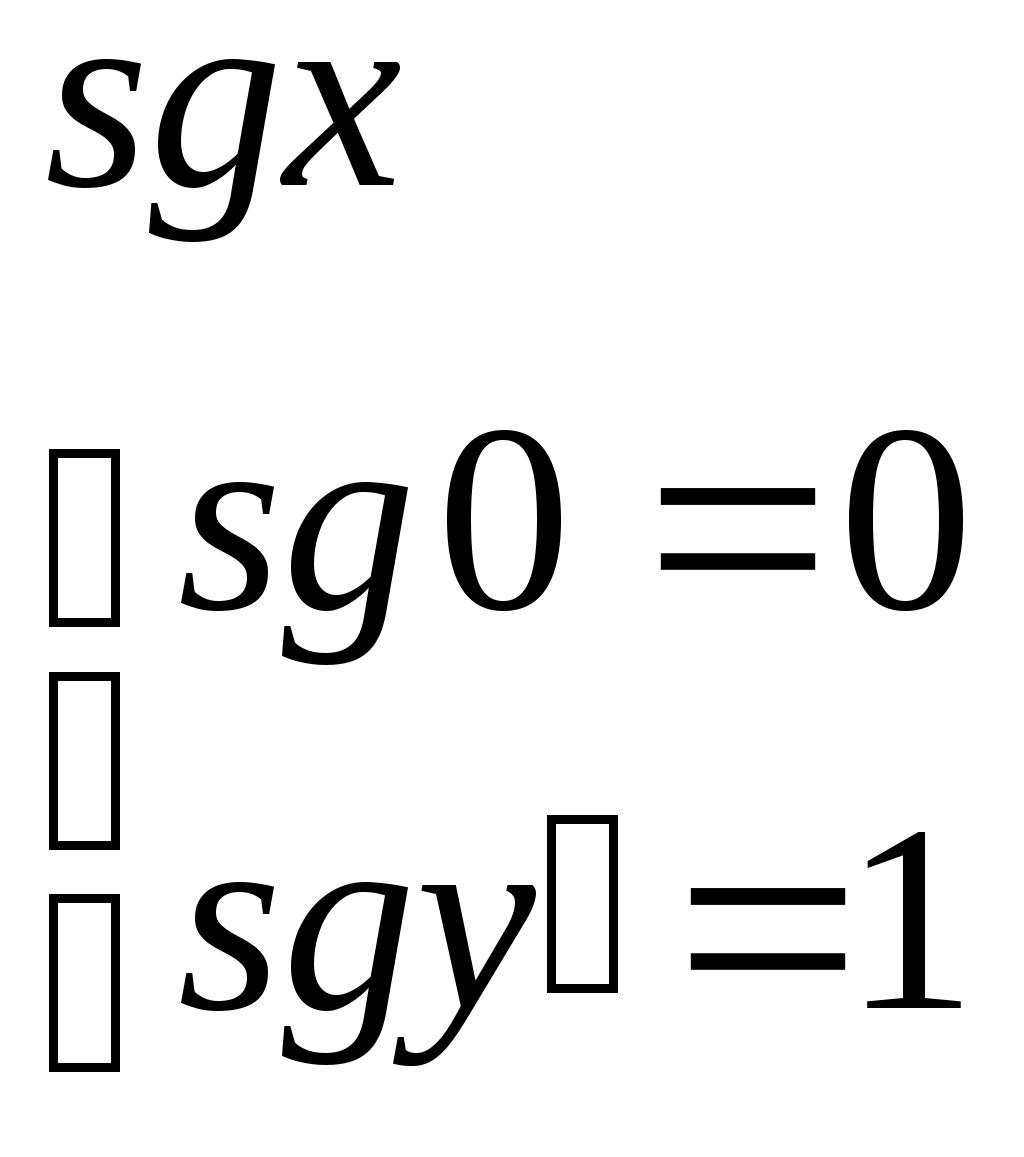

,

А также функций f(x,y)=x^y, f(x)=x!.

Определение 4.1.2. Транзитивное замыкание множества базисных функций относительно операторов суперпозиции функций и примитивной рекурсии называется классом примитивно рекурсивных функций.

Определение 4.1.3. Говорят, что функция f(x₁,x,₂,…x_n) получена из функций g(x₁,x,₂,…x_n, z) и (x₁,x,₂,…x_n) с помощью ограниченного оператора минимизации (ограниченного -оператора) и обозначают:

f(x₁,x,₂,…x_n)= z[g(x₁,x,₂,…x_n, z)=0],

если f(x₁,x,₂,…x_n)= z(x₁,x,₂,…x_n)

тогда и только тогда, когда:

g(x₁,x,₂,…x_n, k)0 при k=0, 1, 2, … z–1, и g(x₁,x,₂,…x_n, z)=0.

Теорема 4.1.3. Применение ограниченного -оператора не выводит из класса примитивно рекурсивных функций.
2. Частично-рекурсивные и общерекурсивные функции
Определение 4.2.1. Говорят, что функция f(x₁,x,₂,…x_n) получена из функции g(x₁,x,₂,…x_n, z) с помощью оператора минимизации (-оператора), и обозначают f(x₁,x,₂,…x_n)= z[g(x₁,x,₂,…x_n, z)=0],

если f(x₁,x,₂,…x_n)=zтогда и только тогда, когда g(x₁,x,₂,…x_n, k)0 при k=0, 1, 2, … z–1, и g(x₁,x,₂,…x_n, z)=0.

Оператор минимизации – удобное средство для построения обратных функций. Функция g(x)= y[f(y)=x] – («наименьший yтакой, что, f(y)=x»)является обратной для функции f(x).

Определение 4.2.2. Функция называется частично рекурсивной, если она базисная функция или может быть построена из базисных функций конечным числом применения операторов суперпозиции функций, примитивной рекурсии и -оператора.

Определение 4.2.3. Класс частично рекурсивных функций есть транзитивное замыкание множества базисных функций относительно операторов суперпозиции функций, примитивной рекурсии и -оператора.

Определение 4.2.4. Всюду определенная частичная рекурсивная функция называется общерекурсивной.

Как следует из приведенных определений, любая примитивно рекурсивная функция является общерекурсивной. Обратное неверно.

Первый пример общерекурсивной, но не примитивно рекурсивной функции был построен немецким математиком В.Аккерманом:

В.Аккерман

Доказано, что диагональная функция Аккермана растет быстрее любой примитивно рекурсивной функции.

В то же время, частично рекурсивные (в том числе и общерекурсивные) функции допускают достаточно простое стандартное выражение через примитивно рекурсивные функции (см. следующую теорему).

Теорема 4.2.1 (Клини). Существует такая примитивно рекурсивная функция g(x), что какова бы ни была частично рекурсивная функция F(x₁, …, x_n), найдетсяпримитивно рекурсивная функция f_F(x₁, …, x_n,z) для которой имеет место равенство:

F(x₁, …, x_n)=g(z[f_F(x₁, …, x_n,z)=0].

В то же время, функция f(x)=y[x+1+y=0] – пример частично рекурсивной нигде не определенной функции.

Таким образом, иерархия классов рекурсивных функций может быть описана следующим образом:

– класс общерекурсивных функций строго содержит класс частично рекурсивных функций;

– класс частично рекурсивных функций строго содержит класс общерекурсивных функций.

Лекция № 5. Алгоритмическая теория множеств
1. Перечислимые и разрешимые множества.

2. Перечислимость и вычислимость.
1. Перечислимые и разрешимые множества
При использовании далее терминов «алгоритм», «вычислимая функция» имеется в виду любая возможная их формализация в терминах машин Тьюринга, нормальных алгорифмов или рекурсивных функций. Все рассматриваемые множества – суть подмножества натурального ряда. Дополнением множества MN является множество N\M.

Определение 5.1.1. Множество MN называется разрешимым, если существует алгоритм, позволяющий для каждого nN определить, принадлежит ли это число множеству M или нет. Такой алгоритм называется разрешающим для множества M.

В иной терминологии это определение формулируется так.

Определение 5.1.1*. Множество MN называется разрешимым, если его характеристическая функция: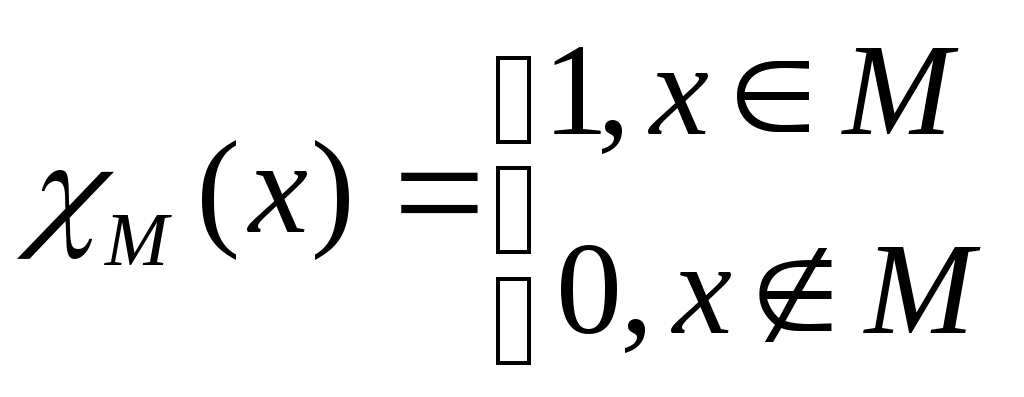



является общерекурсивной.

Теорема 5.1.1. Если множества А и В разрешимы, то разрешимы множества N\А, АВ, АВ.

Доказательство. Если характеристические функции 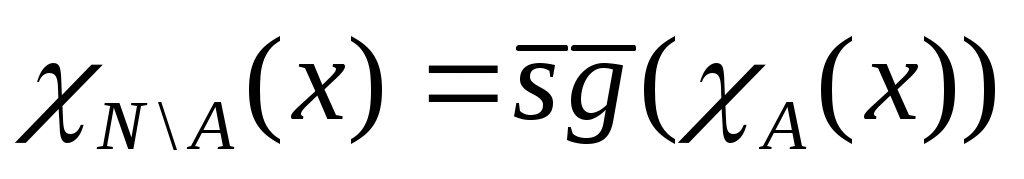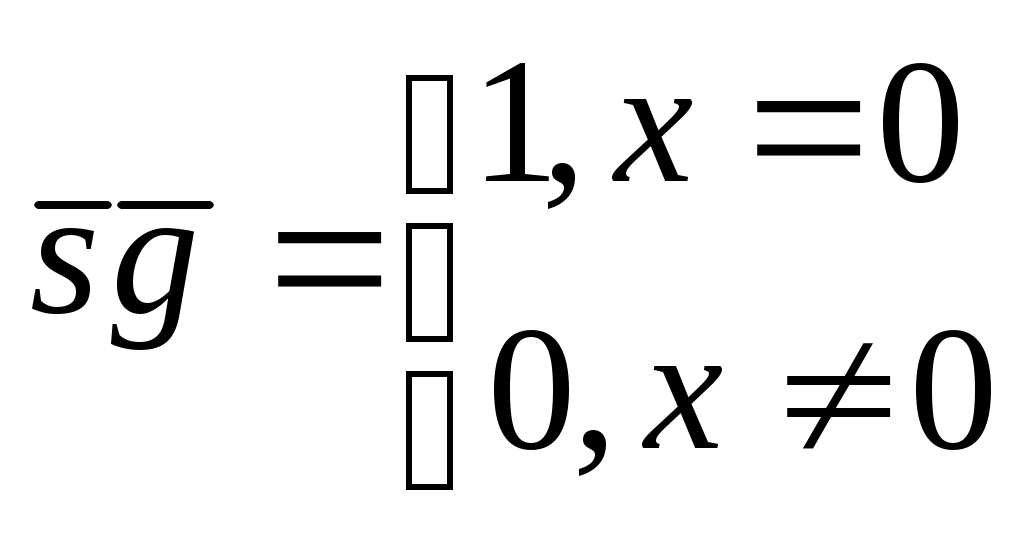и – общерекурсивны, то и характеристические функции множеств N\А, АВ, АВ:

,



.

также являются общерекурсивными функциями.

Теорема 5.1.2. Любое конечное множество MN – разрешимо.

Определение 5.1.2. Непустое множество MN перечислимо, если существует алгоритм, перечисляющий (порождающий) его элементы. Этот алгоритм называют порождающим алгоритмом для множества M.

Пустое множество считается перечислимым по определению.

В терминологии рекурсивных функций приведенное определение формулируется так.

Определение 5.1.2*. Непустое множество MN перечислимо, если существует общерекурсивная функция _M(x) такая, что: M={y: y=_M(x), xN}.

Теорема 5.1.3. Если множества А и В перечислимы, то перечислимо множество АВ.

Доказательство. Положим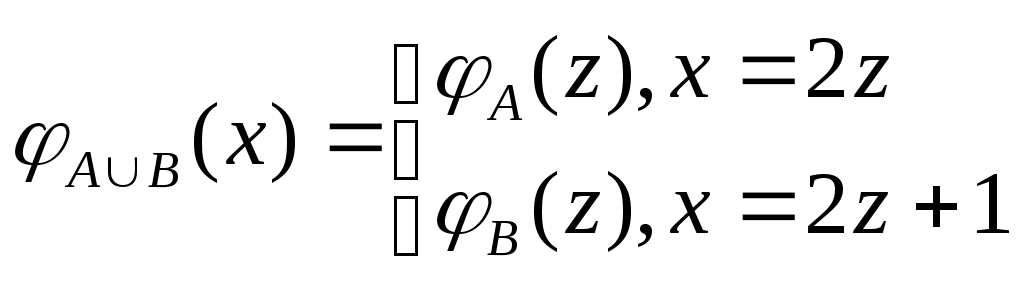



Так как функция rest(x, 2) нахождения остатка от деления xна 2 является общерекурсивной (доказательство этого факта остается за читателем), то общерекурсивной будет и функция: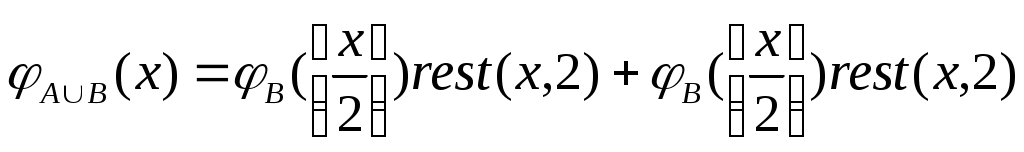

, где – целая часть числа .

В этом случае множество

АВ={y: , xN}

по определению будет перечислимым.

Теорема доказана.

Теорема 5.1.4. Если множества А и В перечислимы, то перечислимо множество АВ.

Доказательство. Введем в рассмотрение следующие функции:

1) функцию ограниченного вычитания: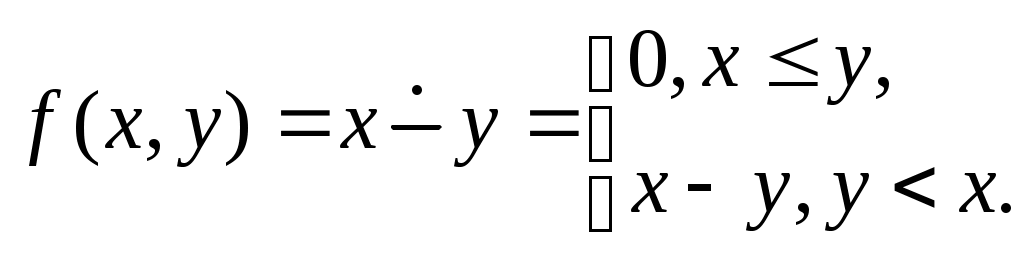





2) функции большого размаха: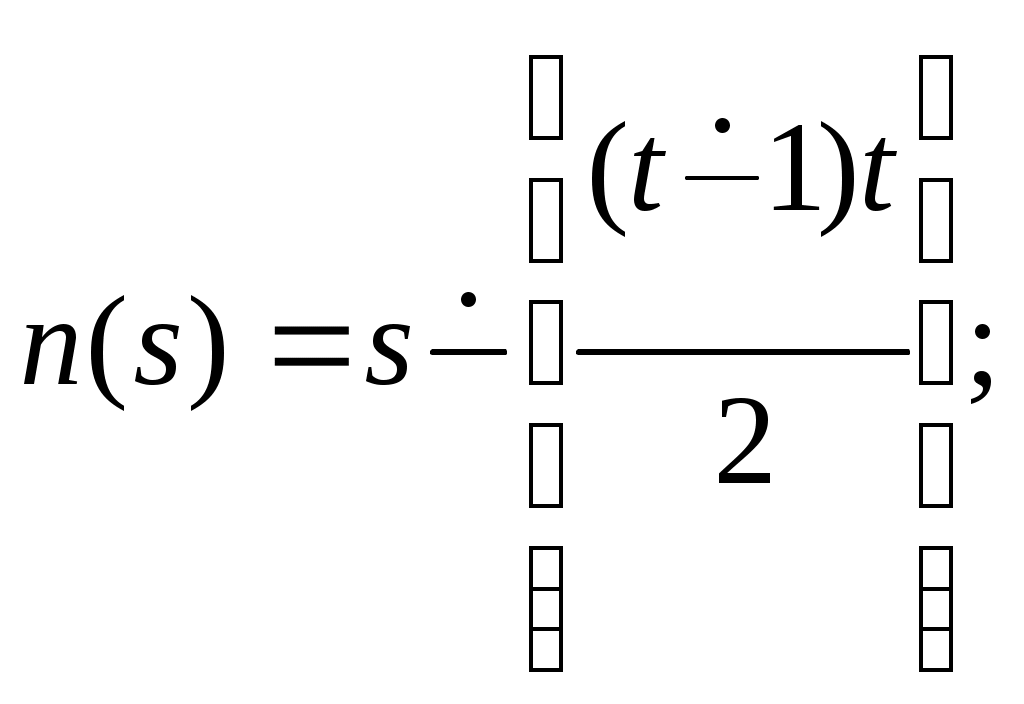



где .

3) где:

_A(x) – общерекурсивная функция, порождающая множество A;

_B(x) – общерекурсивная функция, порождающая множество B;



Все перечисленные функции являются общерекурсивными, и потому общерекурсивной функцией будет функция _AB(x)=_A(n(s(x))), порождающая множество AB.

Теорема доказана.

Теорема 5.1.5. Непустое разрешимое множество MN перечислимо.

Доказательство. Пусть – характеристическая функция множества MN, . Тогда функция



является общерекурсивной и порождающей множество М.

Если М={m₀, m₁,m₂, …, m_n, ..} и m₀,<m₁<m₂ <…<m_n, то график функции 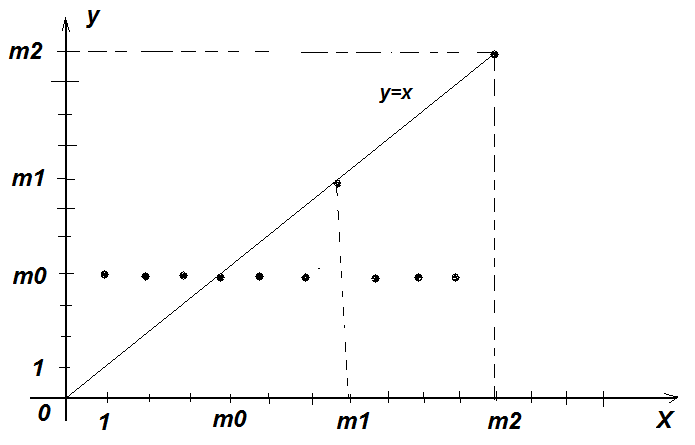имеет вид:



Теорема 5.1.6. Множество MN разрешимо тогда и только тогда, когда M и N\М перечислимы.

Доказательство. Если множество M разрешимо, то по теореме 5.1 разрешимо его дополнение N\М. По теореме 5.4 перечислимы оба множества. В одну сторону теорема доказана.

Пусть далее M и N\М перечислимы, что означает существование общерекурсивных функций _М, _N\М.

Определим общерекурсивную функцию (x), значением которой является наименьшее число z, при котором либо _М(z)=x, либо_N\М(z)=x, следующим образом: .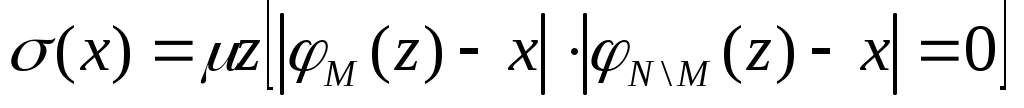

Тогда характеристическая функция множества М может быть записана так: . Так как: общерекурсивная функция, то теорема доказана.

Следствие. Если множество M перечислимо, но неразрешимо, то множество N\М не перечислимо.

Теорема 5.1.7. Множество записей машин Тьюринга является перечислимым множеством.

Теорема 5.1.8. Множество записей самоприменимых машин Тьюринга перечислимо, но не разрешимо.

Следствие. Дополнение множества записей самоприменимых машин Тьюринга неперечислимо.