Лекции по теории алгоритмов. Лекция Интуитивное представление об алгоритме Интуитивное определение алгоритма. Примеры алгоритмов

• Название: Лекция Интуитивное представление об алгоритме Интуитивное определение алгоритма. Примеры алгоритмов
• Анкор: Лекции по теории алгоритмов
• Дата: 05.05.2022
• Размер: 2.84 Mb.
• Имя файла: Лекции по теории алгоритмов.doc
• Тип: Лекция; #513398
• страница: 5 из 7

2. Перечислимость и вычислимость

Определение 5.2.1. График функции y=f(x) – множество

F(x,y)={(x,y): y=f(x), x, yN}

перечислим, если существует алгоритм, перечисляющий входящие в него пары, то есть существуют такие общерекурсивные функции (s), (s), что: F(x,y)={(x,y): x=(s), y=(s), sN}.

Теорема 5.2.1. Функция y=f(x) с непустойобластьюопределения вычислима тогда и только тогда, когда ее график F(x,y)={(x,y): y=f(x), x, yN} является перечислимым множеством.

Доказательство. Пусть график F(x,y) некоторой функции y=f(x) является перечислимым множеством. Тогда перечислимым множеством является P – область определения функции y=f(x): P={x: x=(s), sN}.

Для вычисления f(n) в данной точке nP необходимо.

1. Вычисляя последовательно (0), (1) … , найти первое по порядку число sN такое, что (s)=n. Так какnP, то такое число sобязательно найдется и будет равно

2. Вычислить значение m=(s) и положить f(n)=m.

Таким образом, если график F(x,y) – перечислимое множество, то y=f(x) – вычислимая функция, которая определяется так:



Заметим, что вычисление значения функции в точке, не принадлежащей области определения, приводит к бесконечным вычислениям последовательности (0), (1) … .

Предположим теперь, что функция y=f(x) – вычислима. В этом случае найдется машина Тьюринга T, такая что T(x)=f(x). Тогда в точках, принадлежащих области определения функции, она будет останавливаться и давать точки, принадлежащие графику F(x,y). В точках, не принадлежащих области определения функции, эта машина Тьюринга будет работать бесконечно. Так что график будет перечислимым множеством.

Теорема доказана.

Лекция № 6. Универсальные функции и множества
1. Универсальные функции и множества

2. Главные универсальные функции и множества
1. Универсальные функции и множества
Определение 6.1.1. Функция U двух натуральных аргументов называется универсальной для класса вычислимых функций¹ одного аргумента, если для каждого n функция:

,

является вычислимой функцией, и каждая вычислимая функция одного аргумента встречается среди .

Теорема 6.1.1. Существует вычислимая функция двух аргументов, являющаяся универсальной функцией для класса вычислимых функций одного аргумента.

Доказательство. Пусть p₀, p₁, …p_i,...– последовательность программ², вычисляющих функции одного аргумента. Положим U(i, x) равным результату работы i-ой программы на входе x. ТогдаU(i, x) – универсальнаяфункция.

Теорема доказана.

Определение 6.1.2. Множество называют универсальным для некоторого класса множеств натуральных чисел, если все множества

W_n={x: (n, x)W}

принадлежат этому классу, и других множеств в этом классе нет.

Теорема 6.1.2. Существует перечислимое множество пар натуральных чисел, универсальное для класса всех перечислимых множеств натуральных чисел.

Доказательство. Область определения универсальной функции – универсальное перечислимое множество, так как каждое перечислимое множество есть область определения некоторой вычислимой функции.

Теорема доказана.
Теорема 6.1.3. Не существует вычислимой всюду определенной функции двух аргументов, универсальной для класса всех вычислимых всюду определенных функций одного аргумента.

Доказательство. Пусть U – произвольная вычислимая всюду определенная функция двух аргументов. Положим u(n)=U(n, n), d(n)=u(n)+1. Всюду определенная функция d(n) отличается от всех , а потому U – не является универсальной.

Теорема доказана.

Теорема 6.1.4. Существует вычислимая функция d(n), от которой никакая функция не может отличаться всюду (для любой вычислимой функции найдется nN такое, что f(n)=d(n) (равенство понимается в том смысле, либо оба значения f(n) и d(n) не определены, либо оба определены и равны)).

Доказательство. d(n)=U(n, n), где U(n, х) универсальнаяфункция двух аргументов для класса вычислимых функций одного аргумента.

Теорема доказана.

Теорема 6.1.5. Существует вычислимая функция, не имеющая всюду определенного вычислимого продолжения.

Доказательство. Пусть d(n)=U(n, n), где U(n, х) универсальнаяфункция двух аргументов для класса вычислимых функций одного аргумента. Положим g(n)=d(n)+1. Тогда при тех значениях n, гдефункция d(n) определена g(n)d(n) и любое ее продолжение отличается от d. В этом случае предположение о вычислимости всюду определенного продолжения g(n) придет в противоречие с предыдущей теоремой, гласящей об отсутствии вычислимой функции, всюду отличающейся от d(n).

Теорема доказана.

Теорема 6.1.6. Существуетперечислимое неразрешимое множество.

Доказательство. Область определения F вычислимой функции f(x), не имеющей всюду определенного вычислимого продолжения – перечислимое неразрешимое множество. С одной стороны F – перечислимо.С другой стороны, если бы множество Fбыло бы разрешимо, то функция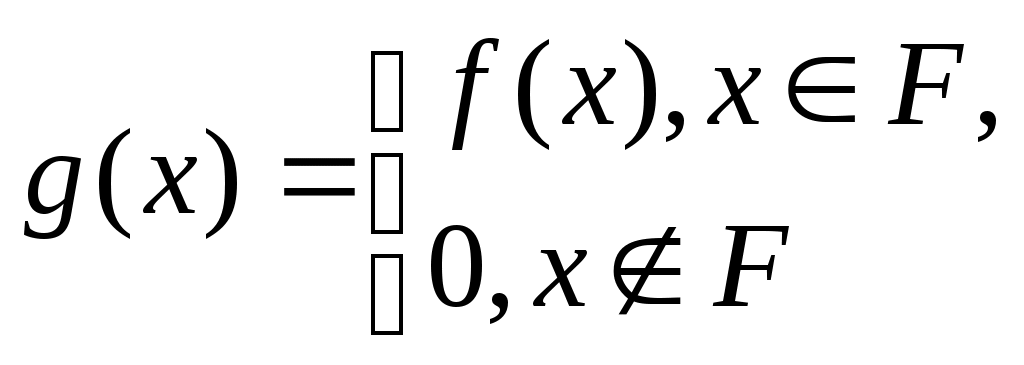



была бы всюду определенным продолжением f(x).

Теорема доказана.

2. Главные универсальные функции и множества
Определение 6.2.1. Универсальная функция U двух натуральных аргументов называется главной универсальной функцией, если для любой вычислимой функции V существует всюду определенная вычислимая функция s(m), для которой V(m, x)=U(s(m), x) при всех mиx(значения VиUлибообане определены, либо определены и равны).

Теорема 6.2.1. Существует главная универсальная функция.

Доказательство. Зафиксируем некоторое взаимнооднозначное соответствие , обозначая номер пары (u, v) через [u, v] ((u, v)[u, v]).

Пусть далее R(x,y) – вычислимая универсальная функция для вычислимых функций одной переменной. Положим T(n, u, v)=R(n, [u, v]).

Если V(u, v) – произвольная вычислимая функция двух аргументов, то функция f([u, v])=V(u, v) – вычислимая функция одного аргумента, и поскольку R(x,y) – универсальна, то найдется число n, для которого R(n, x)=f(x) длялюбыхx. Для этого nвыполнены равенства

T(n, u, v)=R(n, [u, v])=f([u, v])=V(u, v).

Определим U([n, u], v)=T(n, u, v). Тогда согласно предыдущим рассуждениям для произвольной вычислимой функции двух аргументов V(u, v) можнонайти число n, для которого V(u, v)=T(n, u, v)=U([n, u], v) длявсех uиv. Полагая s(u)=[n,u], имеем V(u, v)=U(s(u), v)).

Теорема доказана.

Теорема 6.2.2. Пусть U(u, v) – главная универсальная функция для класса вычислимых функций одного аргумента. Тогда существует всюду определенная функция c(p, q) такая, что U(c(p, q), x)=U(p, U(q, x)) для всех p, qиx.

Доказательство. Положим V([p, q], x)=U(p, U(q, x)). По определению главной универсальной функции найдется такая всюду определенная вычислимая функция одного аргумента s(m), что V(m, x)=U(s(m), x)) для всех m иx.

Тогда функция c(p, q)= s([p, q]) будет искомой.

Теорема доказана.

Теорема 6.2.3. Пусть U(u, v) – универсальная функция для класса вычислимых функций одного аргумента. Если существует всюду определенная функция c(p, q) такая, что U(c(p, q), x)=U(p, U(q, x)) для всех p, qиx, тофункция U(u, v) являетсяглавной универсальной функцией.

Определение 6.2.2. Перечислимое множество называется главным универсальным перечислимым множеством (для класса всех перечислимых подмножеств N), если для любого другого перечислимого множества найдется такая всюду определенная функция s: NN, что для всех n, x

(n, x)V  (s(n), x) W.

Теорема 6.2.3. Существует главное универсальное перечислимое множество .

Доказательство. Пусть U(u, v) – главная универсальная функция для класса вычислимых функций одного аргумента, W – ее областьопределения. Пусть далее – произвольное перечислимое множество. Тогда найдется вычислимая функция G(u, v) с областью определения V. Так как функция U(u, v) – главная универсальная функция, то найдется такая всюду определенная вычислимая функция s(n): NN, что G(n,x)=U(s(n), v) длявсех n, x. Это означает,что (n, x)V (s(n), x) W.

Таким образом, можно утверждать, что область определения главной универсальной функции для класса вычислимых функций одного аргумента является главным универсальным перечислимым множеством для класса перечислимых подмножеств N.

Теорема доказана.

Теорема 6.2.4. Пусть – главное универсальное перечислимое множество, W_n={x: (n, x)W}. Тогда существует такая вычислимая, всюду определенная функция s(m, n), что W_{s(m, n)}=W_mW_n.

Для доказательства теоремы необходимо определить множество V={([m, n], x): xW_mW_n, [m, n] – номер пары}, а затем воспользоваться определением главного универсального множества.

Лекция № 7. Нумерации и их свойства
1. Нумерации.

2. Теорема о неподвижной точке
1. Нумерации
Определение 7.1.1. Всюду определенное отображение : NFобласть значения, которого есть все множество F, называют нумерацией (натуральной нумерацией) множества F. При этом, если (n)=f, то n – номер объекта fF.

Пример 7.1.1. Всякая универсальная функция двух аргументов для класса вычислимых функций одного аргумента задает нумерацию этого класса.

Определение 7.1.2. Нумерации, соответствующие главным универсальным функциям, называют главными или геделевыми.

Теорема 7.1.1. Пусть U – главная универсальная функция. Тогда множество тех n, при которых U_nявляется нигде не определенной, неразрешимо.

Доказательство. Пусть K – перечислимое неразрешимое множество. Рассмотрим вычислимую функцию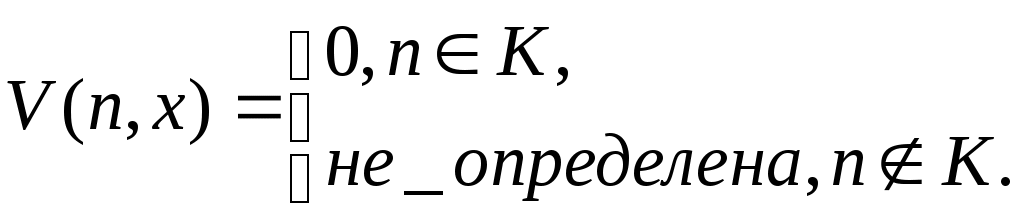



Так как U – главная универсальная функция, то существует вычислимая всюду определенная функция s(n), значениемкоторой при nKявляется U-номер нигде не определенной функции.

Предположим теперь, что множество U-номеров нигде не определенной функции разрешимо. В этом случае разрешимым оказывается и множество K, что приводит к противоречию.

Следствие. Нигде не определенная функция в любой главной нумерации имеет бесконечно много номеров.

Следствие. Множество номеров нигде не определенной функции не только не разрешимо, но и не перечислимо.

Пример 7.1.2 ( вычислимой универсальной функции, не являющейся главной)

Пусть U(n, x) – произвольнаявычислимаяуниверсальная функция, D – множество U-номеров всех функций с непустой областью определения. Пусть d – всюду определенная вычислимая функция, перечисляющая множество D(то есть D={d(0), d(1), …}). Рассмотрим функцию V(i, x), для которой V(0, x) не определена при всех x, аV(i+1, x)=U(d(i), x). Функция V(i, x) вычислима, она универсальна по построению, и единственным V – номером нигде не определенной функции является число 0.

Существуют и другие нумерации. Например, можно построить универсальную вычислимую функцию, для которой каждая вычислимая функция будет иметь ровно один номер (теорема Фридберга). Соответствующие нумерации называют однозначными. Главными эти нумерации быть, очевидно, не могут.

Теорема 7.1.2. (Успенского-Райса). Пусть F – класс вычислимых функций одного аргумента, AF (A, AF). U – главная универсальная функция для F. Тогда множество {n: U_nA} – неразрешимо.

Доказательство. Пусть K – перечислимое неразрешимое множество. Без ограничения общности можно считать, что нигде не определенная функция A. Обозначимчерезпроизвольнуюфункцию, не принадлежащую A (A)¹.

Положим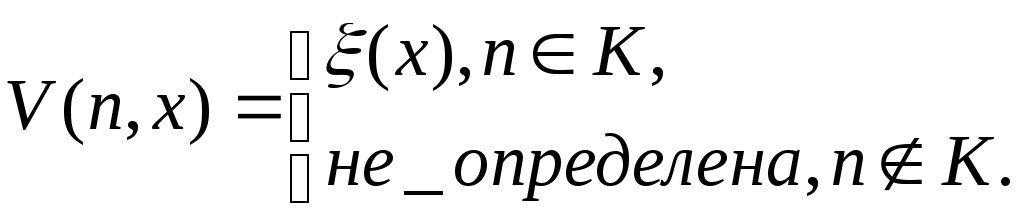



Вычислимая функция V(n, x) при nKсовпадает с  . При nK – с функцией . При этом предположение о разрешимости множества {n: U_nA} влечет за собой утверждение о том, что множество К разрешимо. Полученное противоречие доказывает теорему.

Теорема доказана.

Согласно иной интерпретации теоремы Успенского-Райса можно говорить о том, что по U-номеру вычислимой функции fв главной нумерации нельзя определить обладает ли эта функция некоторым нетривиальным свойством A².

По теореме Успенского-Райса в любой главной нумерации множество номеров любой конкретной функции неразрешимо и потому бесконечно. Справедливо и более сильное утверждение – по номеру любой функции в главной нумерации можно алгоритмически получить бесконечное число других номеров той же функции. Справедлива следующая теорема.

Теорема 7.1.3. Пусть U – главная универсальная функция. Тогда существует такая всюду определенная функция g(i, x), что для любого iчислаg(i, 0), g(i, 1),… образуютпоследовательность различных U-номеров функции U_i.

Теорема 7.1.4. (об изоморфизме главных нумераций). Пусть U₁, U₂ – главные универсальные функции для класса вычислимых функций одного аргумента. Тогда существуют две всюду определенные взаимно обратные вычислимые функции s₁₂, s₂₁ для которых

U₁(n, x)=U₂(s₁₂(n), x) и U₂(n, x)=U₁(s₂₁(n), x).

Доказательство. Укажемалгоритм построения биекции между числами a_i и b_i, считая, что для каждого i числа a_i и b_i,– номера одной и той же функции (a_iв U₁, b_iв U₂).

На каждом шаге построения к соответствиям вида a₁b₁, a₂b₂, …, a_k-1b_k-1 добавляем пару a_kb_k следующим образом.

На четном шаге выбирается наименьшее натуральное число u, не встречающееся в {a₁, a₂, …, a_k-1}. В нумерации U₁ числоu – номер некоторой функции f. Так как нумерация U₂ главная, то, согласно предыдущей теореме отыщется число v{b₁, b₂, …, b_k-1}, которое будет номером функции fв нумерации U₂. Тогда, полагая a_k=u, b_k=v, получимследующую парунашего соответствия.

На нечетном шаге выбирается наименьшее натуральное число v{b₁, b₂, …, b_k-1}, по которому определяется функция g, имеющая в нумерации U₂ номер v. Далеепо функции gотыскивается ее номер u в нумерации U₁,не встречающийсяв {a₁, a₂, …, a_k-1}. Полагая a_k=u, b_k=v, получим следующую парунашего соответствия.

При реализации этого алгоритма с обеих сторон будут включены все натуральные числа, причем построенное соответствие будет вычислимым.

Теорема доказана.

Определение 7.1.3. Функция с натуральными аргументами и значениями, имеющая конечную область определения, называется образцом.

Если t – некоторый образец, то через (t) обозначим множество всех вычислимых функций, являющихся продолжениями t. Пусть далее Т – произвольное множество образцов, (Т) – множество всех вычислимых функций, которые продолжают хотя бы один образец из Т ( ).

Теорема 7.1.5. Пусть Т – произвольное перечислимое множество образцов, U – вычислимая универсальная функция для класса вычислимых функций одного аргумента. Тогда множество всех U-номеров всех функций из (Т) перечислимо.

Теорема 7.1.6. Пусть U – главная универсальная функция для класса вычислимых функций одного аргумента. Пусть G – некоторое подмножество этого класса. Если множество {n: U_nG} перечислимо, то G=(Т) для некоторого перечислимого множества образцов Т.
2. Теорема о неподвижной точке
Теорема 7.2.1. Пусть U – главная вычислимая универсальная функция для класса вычислимых функций одного аргумента, h(x) – произвольная всюду определенная вычислимая функция одного аргумента. Тогда существует такое число n, U_n=U_h(n), то есть n и h(n) – номера одной функции.

Приведенная теорема называется теоремой Клини о неподвижной точке или теоремой о рекурсии.

Классическим следствием теоремы о рекурсии выступает утверждение о том, что существует программа, печатающая на любом входе свой собственный текст. Это следствие формулируется в виде следующей теоремы.

Теорема 7.2.2. Пусть U(n, x) – главнаявычислимаяуниверсальная функция для класса всех вычислимых функций одного аргумента. Тогда существует такое числоp, что U(p, x)=pдля любогоx.

Теорема 7.2.3. Если W – главное универсальное перечислимое множество, то всякая вычислимая всюду определенная функция h имеет неподвижную точку n, для которой W_n=W_h(n).

Определение 7.2.1. Два множества U₁и U₂ вычислимо изоморфны, если существует биекция (вычислимая перестановка) f: NNтакая, что (x, y)U₁(f(x), f(y))U₂.

Теорема 7.2.4. Любые два главных универсальных множества для класса перечислимых подмножеств натурального ряда вычислимо изоморфны.

Лекция № 8. Тезисы теории алгоритмов
Понятие алгоритма используется в математике давно, но до начала 1920 гг. оно встречалось примерно в таком контексте – для решения такой-то задачи необходимо совершить такие-то действия, чтобы получить искомый результат. В двадцатые годы прошлого столетия математики столкнулись с дачами, для которых они, как ни старались, не могли найти алгоритмы их решения. В математическом сообществе появилась идея, что таких алгоритмов вовсе не существует. Но тут же возникла другая проблема – отсутствие чего следует доказывать. Определение понятия «алгоритм», пригодное для решения многих разнообразных математических задач, в то время отсутствовало. В середине 30-х годов XX века и позднее были предприняты попытки формализации понятия алгоритма – определения универсальной формы записи информации и ограниченного, четко определенного набора элементарных действий по ее переработке, необходимых и достаточных для реализации любого содержательно описанного алгоритма.

Обобщенным результатов этих поисков можно считать следующее утверждение, имеющее естественно-научный характер:

«Тезис формализации. Любой содержательно описанный алгоритм может быть формализован в рамках используемых в теории алгоритмов строгих математических определений понятия алгоритма» [].

Подчеркнем, этот тезис, равно как и другие, которые будут перечислены ниже, не является теоремой, поскольку, с одной стороны, имеются строго определенные математические объекты, а с другой – интуитивные представления о том, что есть алгоритм.

Это обстоятельство становится особенно ясным, если определить понятие интуитивно вычислимой функции примерно следующим образом:

«функция f(x) – интуитивно вычислима, если для вычисления ее значений существует алгоритм».

В этом контексте Тезис Черча-Клини о том, что класс интуитивно вычислимых функций» совпадает с классом «частично рекурсивных функций», есть ни что иное, как предположение о том, что:

– если мы хоть как-то можем вычислить некоторую функцию f(x), то она либо базисная, либо может быть построена из базисных функций конечным числом применения операторов суперпозиции функций, примитивной рекурсии и -оператора (т.е. путем конечного применения ограниченного набора операций);

– если функция f(x) – не является частично-рекурсивной (а такие функции существуют), то она не является интуитивно вычислимой, а потому ее вычисление является алгоритмически неразрешимой проблемой.

Этот тезис называют основной гипотезой теории алгоритмов. В ее пользу приводят множество доводов, важнейшим из которых выступает то обстоятельство среди множества интуитивно вычислимых функций, накопившихся за годы развития математики, не нашлось ни одной, о которой можно было бы сказать, что она не принадлежит к классу частично рекурсивных функций.

Существуют и другие тезисы теории алгоритмов. Вот некоторые из них.

Тезис Тьюринга. Любой вербальный алгоритм в алфавите M может быть реализован некоторой машиной Тьюринга, работающей над алфавитом M.

Тезис Маркова – принцип нормализации. Любой вербальный алгоритм в алфавите M может быть реализован некоторым нормальным алгорифмом над алфавитом M.

О том, что эти два тезиса справедливы (или не справедливы) одновременно, гласит следующая теорема.

Теорема 8.1. Для любой машины Тьюринга (Т) в алфавите М существует нормальный алгорифм (N) над алфавитом М такой, что для всех М^*, N()=Т(). Для любого нормального алгорифма (N) в алфавите М существует машина Тьюринга (Т) над алфавитом М такая, что для всех М^*, Т()=N().

Еще один тезис теории алгоритмов звучит так.

Тезис Черча-Тьюринга. Всякая интуитивно вычислимая функция является вычислимой по Тьюрингу.

Соответственно, справедлива следующая теорема.

Теорема 8.2. Функция f(x₁, …, x_n) частичнорекурсивна тогда и только тогда, когда она вычислима по Тьюрингу.

Иными словами, рассмотренные подходы к формализации понятия алгоритм (в терминах рекурсивных функций, машины Тьюринга, алгорифмов Маркова), согласно приведенным теоремам, в принципе эквивалентны.

Более того, следует сказать, что в рамках теории алгоритмов были разработаны различные способы уточнения понятия «вычислимость» с использованием аппарата:

1) -определимых функций (А.Черч, С.К.Клини, 1933–1936 гг.);

2) общерекурсивных функций (Ж.Эрбан, К.Гедель, С.К.Клини, 1934–1936 гг.);

3) -рекурсивных и частично рекурсивных функций (К.Гедель, С.К.Клини, 1934–1936 гг.);

4) машин Тьюринга (А.Тьюринг, 1936 г.);

5) машины Поста (Э.Пост, 1943 г.);

6) нормальных алгорифмов Маркова (А.А.Марков, 1950);

7) МНР-вычислимых функций (Дж.Шепердсон, Х.Стерджис, 1963).

Однако, несмотря на значительные различия в подходах при описании вычислимости, каждое из перечисленных уточнений понятия «вычислимость» приводит к одному и тому же классу вычислимых функций. Заметим, что этот результат рассматривается в теории алгоритмов как серьезное подтверждение справедливости тезисов этой теории. С прагматической точки зрения данный результат означает ровно одно. Если функция не вычислима в соответствии с каким-то из указанных подходов, то она не может быть вычислена в рамках иной другой из указанных формализаций.

Помимо этого, приведенные формализации понятия «алгоритм» позволяют говорить о существовании алгоритмически неразрешимых проблем.