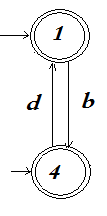Лекции по теории алгоритмов. Лекция Интуитивное представление об алгоритме Интуитивное определение алгоритма. Примеры алгоритмов

• Название: Лекция Интуитивное представление об алгоритме Интуитивное определение алгоритма. Примеры алгоритмов
• Анкор: Лекции по теории алгоритмов
• Дата: 05.05.2022
• Размер: 2.84 Mb.
• Имя файла: Лекции по теории алгоритмов.doc
• Тип: Лекция; #513398
• страница: 7 из 7

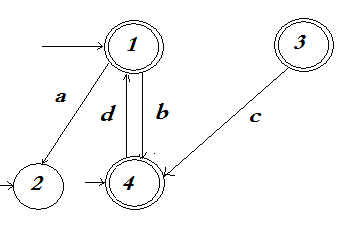
Лекция № 10. Праволинейные языки и конечные автоматы
1. Конечные автоматы

2. Характеризация праволинейных языков
1. Конечные автоматы
Наиболее распространенными способами конечного задания формального языка являются грамматики и автоматы. Здесь рассматриваются конечные автоматы, соответствующие в иерархии Хомского праволинейным грамматикам.

Определение 10.1.1. Конечный автомат – это пятерка

M=<Q, A, D, I, F>, где:

а) Q – конечное множество, именуемое множеством состояний, элементы которого называются состояниями и, как правило, либо нумеруются, либо просто обозначаются числами;

б) A – конечный входной алфавит (или просто алфавит);

в) D – конечное подмножество декартового произведения:

DQA^*Q,

причем элемент множества Dвида <p, x, q> – называется переходом из состояния p в состояние q, а слово x – меткой этого перехода;

г) I – конечное множество начальных состояний (IQ);

д) F – конечное множество заключительных (допускающих) состояний (FQ).

Пример 10.1.1. Пусть Q={1, 2, 3, 4}, A={a, b}, I={1}, F={4}, D={<1,a,2>, <1,b,3>, <2,a,2>, <2,b,2>, <3,a,3>, <3,b,3>, <2,b,4>, <3,a,4>}. Тогда M₁=<Q, A, D, I, F> – конечный автомат.

Конечные автоматы допускают описание в виде диаграмм состояний (диаграмм переходов). Каждое состояние обозначается кружком, причем начальное состояние распознается по ведущей в него короткой стрелке, а заключительное состояние отмечается двойным кружком. Переходы на диаграмме обозначаются стрелками. Стрелка из состояния p в состояние q, помеченная словом x, фиксирует наличие перехода <p, x, q>.

Например, диаграммаконечного автоматаM₁ имеет следующий вид: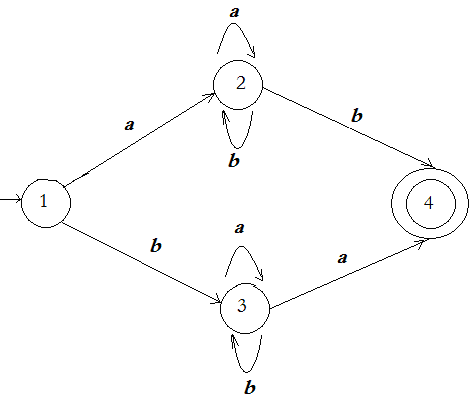



Рис. 10.1.1. Диаграмма переходов конечного автомата М₁

Определение 10.1.2. Путь конечного автомата – это кортеж вида <q₀, <q₀, w₁, q₁>, q₁, <q₁, w₂, q₂>, q₂…, q_i-1, <q_i-1, w_i, q_i>, q_i,…q_n>, где n0 идля всехi<q_i-1, w_i, q_i>D, q_iQ, w_iA^*. При этом:

а) q₀ – начало пути; б) q_n– конец пути;

в) n – длина пути; г) w₁w₂,…, w_i, … w_n– метка пути.

Путь называется успешным, если q₀I, а q_nF.

Пример 10.1.2. Рассмотрим конечный автомат М₁ из примера 10.1.1. Путь <1, <1, a, 2>, 2, <2, b, 2>, 2, <2, b, 4>, 4> – успешный.

Меткой этого пути будет слово abb, длина пути равна 3.

Определение 10.1.3. Слово w допускается конечным автоматом М, если оно является меткой некоторого успешного пути.

Пример 10.1.3. Рассмотрим конечный автомат М₁ из примера 10.1.1. Слова abb, abbabbabb, baba, ba – допускаютсяавтоматом М₁, а слова aba, abbabbaba, bab, bbb – недопускаютсяавтоматом М₁.

Определение 10.1.4. Множество всех слов, допускаемых конечным автоматом, называется языком, распознаваемым конечным автоматом М. Обозначается этот язык L(M). Также говорят, что автомат М распознает язык L(M).

Пример 10.1.4. Конечный автомат М₁ из примера 10.1.1 распознаетязык L(M₁)={awb: wA^*}{bwa: wA^*} (заметим, что L(M₁) – представляет собоймножествослов, у которых первая и последняя буквы не совпадают).

Пример 10.1.5. ПустьМ₂=<Q, A, D, I, F>, где Q={1, 2}, I={1}, A={a, b}, F={1, 2}, D={<1, a, 2>, <2, b, 1>}. Диаграмма переходов конечного автомата М₂ имеет вид: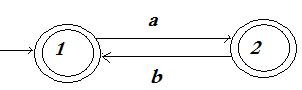



Рис. 10.1.2. Диаграмма переходов конечного автомата М₂

Тогда L(M₂)={(ab)ⁿ: n0}{(ab)ⁿa: n0 }.

Определение 10.1.5. Два конечных автомата эквивалентны, если они распознают один и тот же язык.

Пример 10.1.6. Конечныеавтоматы, представленные следующими диаграммами (рис. 10.1.3), эквивалентны.

Рис. 10.1.3. Диаграммы переходов эквивалентных конечных автоматов

Определение 10.1.6. ЯзыкLназывается автоматным, еслисуществует конечный автомат, распознающий этот язык.

Определение 10.1.7. Состояниеq достижимо изсостояния p, если существует путь, началом которого является p, а концом – q.

Теорема 10.1.1. Каждый автоматный язык распознается некоторым конечным автоматом, в котором каждое состояние достижимо из некоторого начального состояния и из каждого состояния достижимо хотя бы одно заключительное состояние.

Иными словами, каждый конечный автомат может быть преобразован в эквивалентный автомат, в котором каждое состояние достижимо из некоторого начального состояния и из каждого состояния достижимо хотя бы одно заключительное состояние. Пример подобного преобразования приведен на рис. 10.1.3.

Теорема 10.1.2. Каждый автоматный язык распознается некоторым конечным автоматом, не содержащим переходов с метками длины больше единицы и имеющим ровно одно начальное состояние и ровно одно заключительное состояние.

Теорема 10.1.3. Каждый автоматный язык распознается некоторым конечным автоматом, содержащим только переходы с метками длины единица и имеющим ровно одно начальное состояние.

Определение 10.1.8. Конечныйавтомат M=<Q, A, D, I, F> называется детерминированным, если:

1) множество начальных состояний I содержит ровно один элемент;

2) длина метки каждого перехода равна единице;

3) для любого символа aA и для любого состояния pQсуществует не более одного состояния qQсо свойством <p, a, q>D.

Примером детерминированного конечного автомата может служить автомат М₂ из примера 10.1.5. Примером недетерминированного конечного автомата может служить автомат М₁ из примера 10.1.1.

Определение 10.1.9. Детерминированный конечныйавтомат M=<Q, A, D, I, F> называется полным, если для каждого состояния pQи для любого символа aAнайдется такое состояниеqQ, что<p, a, q>D.

Теорема 10.1.4. Каждый автоматный язык распознается некоторым полным детерминированным конечным автоматом.

Иными словами, каждому конечному автомату можно сопоставить эквивалентный ему полный детерминированный конечный автомат.

Пример 10.1.7. Диаграмма полного детерминированного конечного автомата, эквивалентного автомату М₁ из примера 10.1.1, выглядит следующим образом: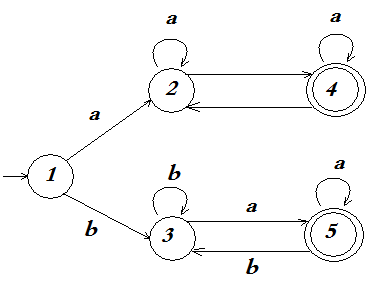



Рис. 10.1.4. Диаграмма полного детерминированного конечного автомата,

эквивалентного автомату М₁

Пример 10.1.8. Диаграмма полного детерминированного конечного автомата, эквивалентного автомату М₂ из примера 10.1.5, выглядит следующим образом: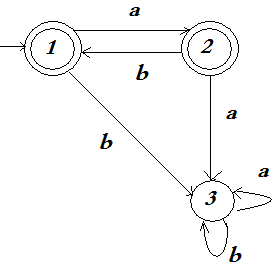



Рис. 10.1.5. Диаграмма полного детерминированного конечного автомата,

эквивалентного автомату М₂
2. Характеризация праволинейных языков
Теорема 10.2.1. Каждый автоматный язык является праволинейным.

Доказательство. Пусть автоматный язык L(M) определяется конечным автоматом М=<Q, A, D, I, F>, где QA=, и I={q₀}. Положим N=Q, S=q₀, P={pxq: <p, x, q>D}{p:pF}. Тогда G=<N, A, P, S> – праволинейная грамматика (грамматика типа 3), порождающая язык L(M).

Теорема доказана.

Теорема 10.2.2. Каждый праволинейный язык является автоматным.

Доказательство. Без ограничения общности можно считать, что праволинейный язык L задан праволинейной грамматикой, не содержащей правил вида Tu, где uA⁺. Положим:

Q=N, I={S}, F={TN: (T)P}, D={<T, u, B> : (TuB)P}.

Тогда конечный автомат М=<Q, A, D, I, F> порождает такой язык L(M), что L=L(M).

Теорема доказана.

Пример 10.2.1. Праволинейный язык

L={w{a, b}^*: w_amod 2=0, w_bmod 2=0}

порождается грамматикой G=<N, A, P, S>, где N={S, T, E, F}, A={a, b}, P={SaT, SbE, S, TaS, TbF, EaF, EbS, FaE, FbD}.

Диаграмма переходов конечного автомата M₃, порождающего этот же язык имеет вид: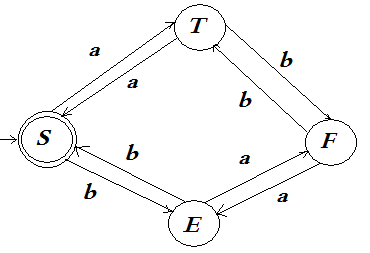


Рис. 10.2.1. Диаграмма конечного автомата М₃

Определение 10.2.1. Праволинейная грамматика, в которой каждое правило имеет вид T, Ta, TaU, где T, UN, aA, называется праволинейной грамматикой в нормальной форме (автоматной грамматикой, регулярной грамматикой).

Теорема 10.2.3. Каждая праволинейная грамматика эквивалентна некоторой праволинейной грамматике в нормальной форме.

Теорема 10.2.4. Классправолинейныхязыков замкнутотносительно итерации, конкатенации и объединения.

Теорема 10.2.5. Классправолинейныхязыков замкнутотносительно дополнения и пересечения.

Теорема 10.2.6. Пусть L – праволинейный язык над алфавитом А. Тогда найдется такое натуральное p>0, что для любого слова wL wpможноподобрать слова x, y, zA^*, длякоторых справедливы соотношения:y, xyp, xyz=w, xyⁱzL(для всех i0).

Пример 10.2.2. ПустьязыкL={abⁿaⁿ: n0} задан над алфавитом A={a, b}.

Пустьp – произвольноенатуральное число. Положимw=ab^pa^p_.

Если положить x=, то возможны следующие варианты:

y	Z	w	xyyz
a	bpap	xyz	aabpapL
abk(0	bp-kap	xyz	abkabpapL
abp	ap	xyz	abpabpapL
abpak(0p)	ap-k	xyz	abpak+1bpapL

Как видно из приведенной таблицы, при любом натуральном pиx=словоxyyzL. С помощью аналогичных выкладок можно придти к выводу о том, что при любом натуральном pи при x=aсловоxyyzL. Этотже вывод оказываетсяверен и приx=ab^k, x=ab^pa^k. В свою очередь, это означает, что условие теоремы 10.2.6 не выполняется, а потому язык L не является автоматным.
Лекция № 11. Контекстно-свободные языки

1 Степанов А.Н. Информатика: Учебник для вузов. 4-е изд. – СПб.: Питер, 2005. – С. 41.

1 Этой теории будут посвящены следующие лекции.

1 В теории нормальных алгорифмов пустое слово обозначается символом .

2  – подслово слова .

1 В ряде источников, например в [], стандартным считается то положение, при котором головка «обозревает» ячейку, в которой записана первая буква слова, т.е. крайне левую ячейку.

1 Здесь и далее в соответствии с тезисами теории алгоритмов под вычислимыми функциями подразумеваются частично рекурсивные функции. Соответственно под всюду определенными вычислимыми функциями – общерекурсивные функции.

2 Эти программы могут, например, располагаться в порядке возрастания их длины.

1 Если в классе А отсутствует нигде не определенная функция, то можно взять произвольную функцию из класса А, а нигде не определенную функцию из его дополнения.

2 Не тривиальным в том плане, что класс всех вычислимых функций разбивается на два непустых подкласса функций, обладающих и не обладающих этим свойством.