Лекция 1 Приближённые методы решения слау
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
В) Модификации метода Эйлера. 1ый усовершенствованный метод Эйлера. Сначала вычисляют промежуточные значения: 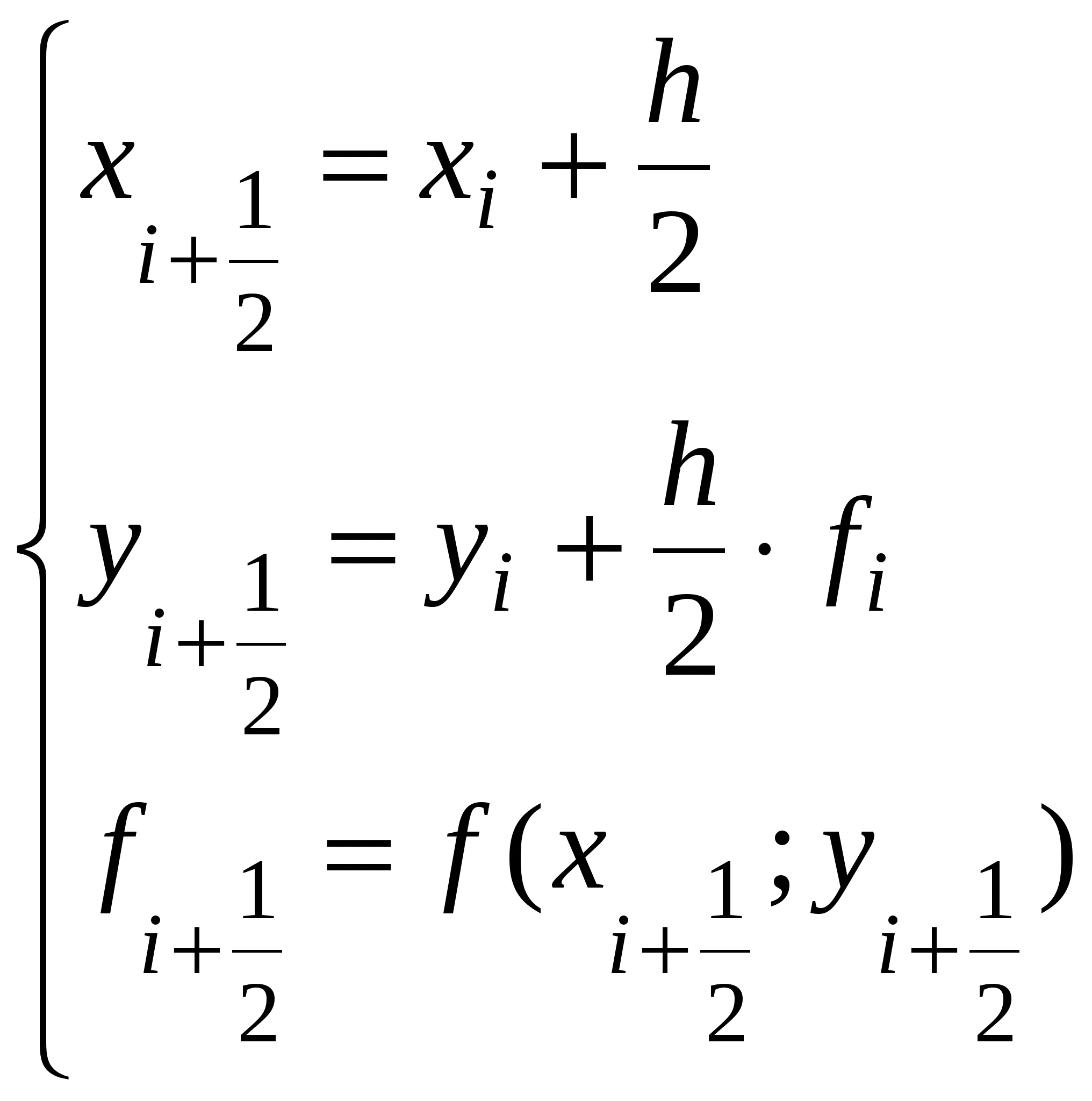 (9) (9)А затем полагают: 2oй усовершенствованный метод Эйлера. Сначала определяют «грубые приближения»: 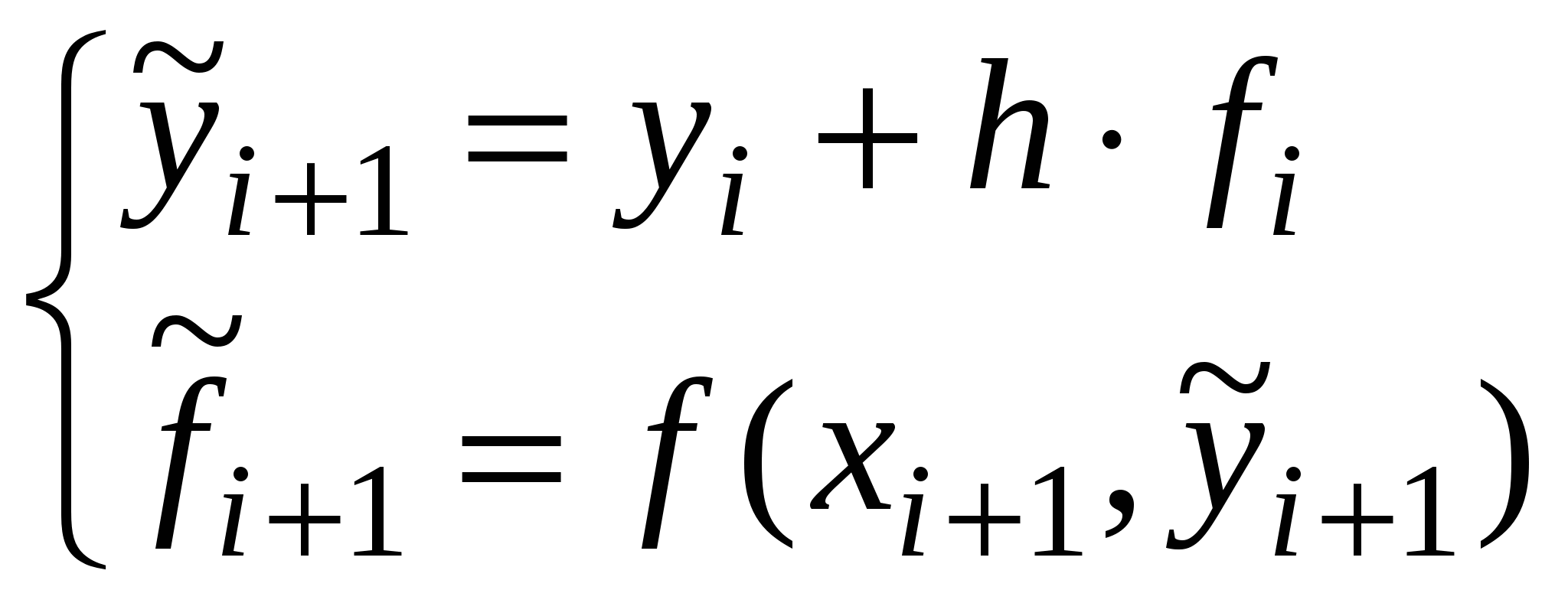 (11) (11)И приближённо полагают: Локальная погрешность на i-ом шаге: С.) Метод Рунге-Кутта. (4го порядка) Наиболее знаменитым из методов Рунге-Кутта является классический метод 4го порядка Грубая оценка погрешности (двойной просчёт): Где у(хi) – точное решение, у*i – приближённое решение с шагом h/2, yi – … с шагом h . Для оценки правильности выбора шага h используют равенство: 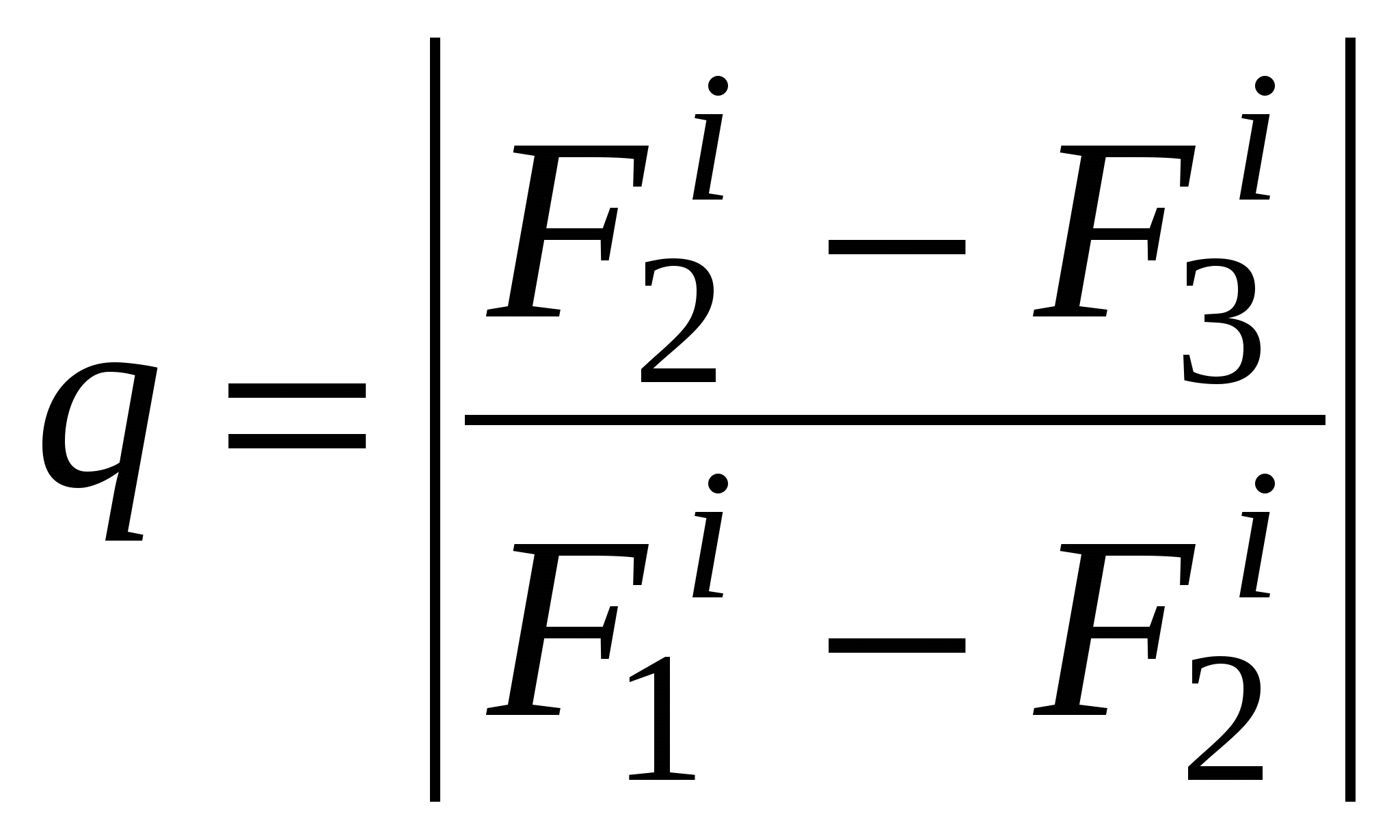 (17) (17)q должно равняться нескольким сотым, иначе h уменьшается. D). Метод Рунге–Кутта 3-го порядка Многошаговые методы. (используют информацию о нескольких предыдущих точках) Д ) Алгоритм Адамса. Пусть дано дифференциальное уравнение: у′ = f(x, y) (1) с начальными условиями: у(х0) = у0 (1*) Требуется найти решение уравнения (1) на отрезке [a,b]. Разобьём отрезок [a,b] на n равных частей точками хi = х0 + ih (i =0, 1, …, n). 1ый этап: стартовая процедура. Используют какой-либо одношаговый метод того же порядка точности до тех пор, пока не будет получено достаточно значений для работы многошагового метода. Следовательно, определены: у1, у2, …, уk-1 в точках: х0 + h, …, x0 + h(k-1). 2ойэтап: рекурсивной процедуры. Определение: уk, yk+1,…, yn основано на интегрировании интерполяционного многочлена Ньютона. Рабочие формулы явных методов Адамса (2-го, 3-го, 4-го порядков). Формулы (2)-(4) называются экстраполяционными и на практике используются в качестве прогноза. Для улучшения точности или коррекции результата применяют неявные методы (используют ещё ненайденные значения: уk+1, yk+2,…). Формулы (5)-(7) называются интерполяционными. Для грубой оценки точности (двойной просчёт): |
