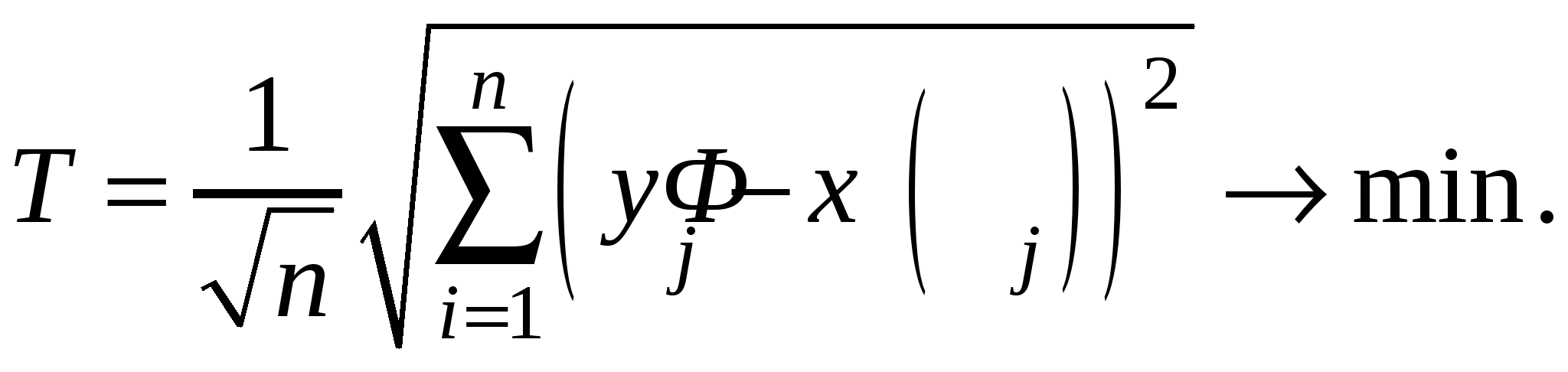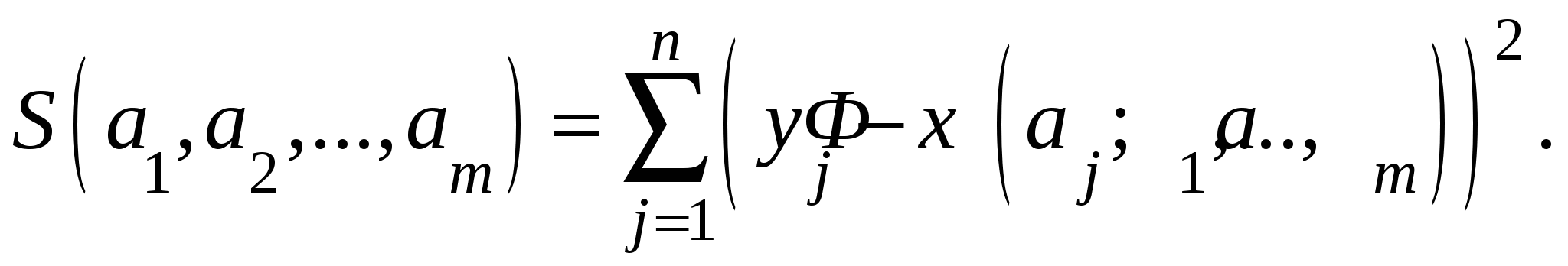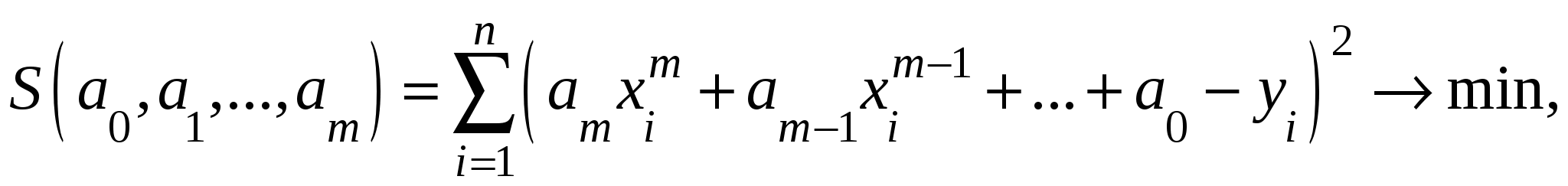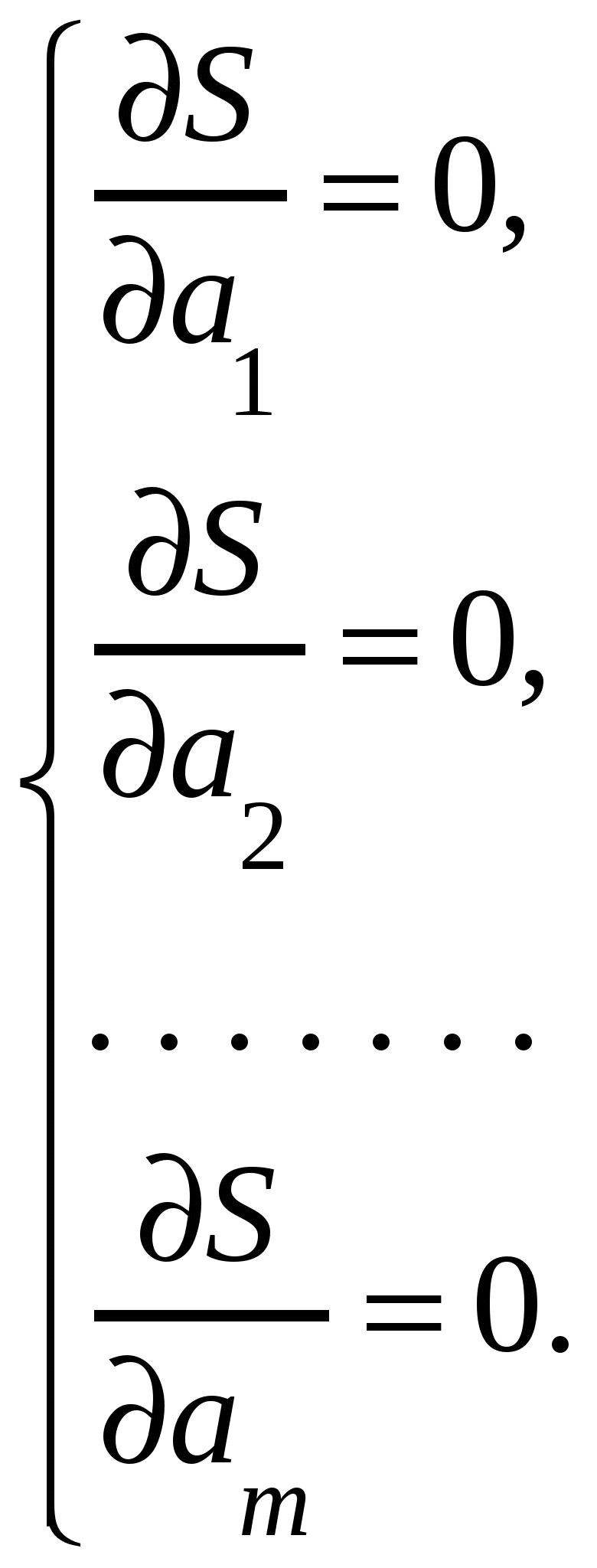Лекция 1 Приближённые методы решения слау
 Скачать 0.74 Mb.
|
|
Оценка погрешности:  ; -n ≤ t ≤ 0; x є [x0;xn], μ=max│f(n+1)(x)│С.) «МЕТОД НАИМЕНЬШИХ КВАДРАТОВ» Перечислим особенности, на которые надо обратить внимание при выполнении задания по этой теме. Предполагается, что функция  задана в виде таблицы конечного числа точек
например, получена экспериментально, где xi, yi (i=1,…,n) – произвольные числа. При этом все числа xi различны. Пусть также имеется некоторая функция  , определенная для всех значений xi (i=1,…,n).Определение 3. Число Т, где
называется среднеквадратичным (или среднеквадратическим) уклонением функции  от заданной  .Наряду с числом Т вводят также вспомогательную величину
Функцию стараются подобрать, чтобы число Т получилось достаточно малым. Можно предложить следующие способы выбора функции .Способ 1.  , (9)т.е. - многочлен степ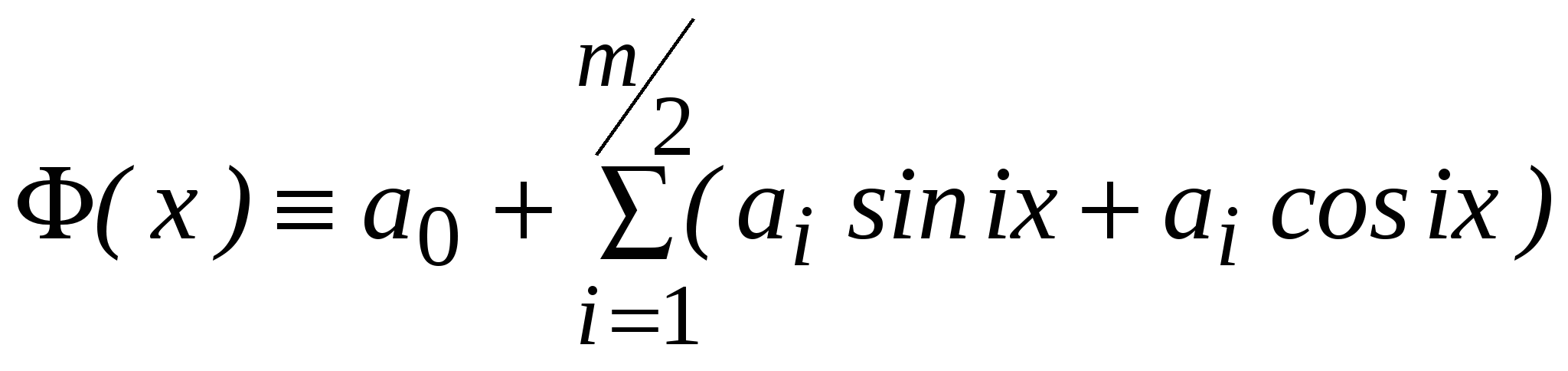ени m, при этом m<n.Способ 2.  , здесь - сплайн, т.е. кусочно-полиномиальная гладкая функция.Способ 3.  , (10)т.е. - частичная сумма ряда Фурье, при этом m – четно и m<n.Перечисленные способы 1-3 задают для вид приближающей функции , которая, в свою очередь, зависит от коэффициентов (или параметров) ai. Лучшим набором коэффициентов ai считается тот, для которого величина w из (8) меньше.Определение 4. Говорят, что функция найдена для по методу наименьших квадратов (МНК), если она дает минимально возможное значение величины w в соотношении (8).Примечание. Заметим, что при m=n-1 многочлен  , полученный по МНК, совпадает с интерполяционным многочленом и, следовательно, соответствующее среднеквадратичное уклонение (теоретически) равно числу  . При использовании в расчетах ЭВМ это уклонение, как правило, получается числом, отличным от нуля.Рассмотрим в качестве приближающей функции многочлен степени m, который имеет вид  Согласно методу наименьших квадратов наилучшими коэффициентами  считаются те, для которых сумма квадратов уклонений будет минимальной, т. е.
Т есть функция коэффициентов . Наряду с функцией Т рассматривают функцию S вида:
Очевидно, что S и Т достигают своего минимума в одной точке. Далее для отыскания точки минимума будем рассматривать функцию S, поскольку она удобнее для вычислений. При данной приближающей функции критерий близости, который используется в методе наименьших квадратов, запишется следующим образом:
Используя необходимое условие экстремума функции нескольких переменных, получим систему для определения коэффициентов  , где  :
То есть:
Лекция 3 ПРИБЛИЖЁННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ Общие замечания. Если функция f(x) непрерывна на отрезке [a, b] и известна её первообразная F(x), то определённый интеграл от этой функции в пределах от a до b может быть вычислен по формуле Ньютона- Лейбница  , (1)где F′(x) = f(x). Однако во многих случаях первообразная функция F(x) не может быть найдена с помощью элементарных средств или является слишком сложной; вследствие этого вычисление определённого интеграла по формуле (1) может быть затруднительным или даже практически невыполнимым. Кроме того, на практике подынтегральная функция f(x) часто задаётся таблично или графически. Поэтому важное значение имеют приближённые и в первую очередь численные методы вычисления определённых интегралов. Задача численного интегрирования функции заключается в вычислении значения определённого интеграла на основании ряда значений подынтегральной функции. Обычный приём при численном вычислении однократных интегралов. Отрезок [a, b] разбивают на части (чаще всего равные) точками хj ( j =  ) так, что a = x0 < x1 < x2…< xn= b, и в узлах хj находят значения уj = f(xj). Функцию f(x) заменяют интерполирующей или аппроксимирующей функцией простого вида (например, полином) такой, что она легко интегрируется. Мы получаем квадратурные формулы:  , (2)где хj − выбранные узлы интерполяции, Аj − коэффициенты, зависящие только от выбора узлов, но не от вида функции, R − остаточный член, или погрешность квадратурной формулы. 1) Интегрирование по методу прямоугольников. Метод прямоугольников − простейший приём численного интегрирования, при котором функция f(x) заменяется интерполяционным многочленом нулевого порядка. Интервал интегрирования [a,b] делится точками х0, х1, …, хn на n равных частей (рис. 1), причём х0 = a, xn= b, длина каждой части составляет h = (b-a)/n, и тогда xi = x0+ih, i = 0, …, n. Из каждой точки х проведём перпендикуляр до пересечения с кривой f(x), а затем заменим кривую подынтегральной функции ломаной линией, отрезки которой параллельны оси абсцисс. 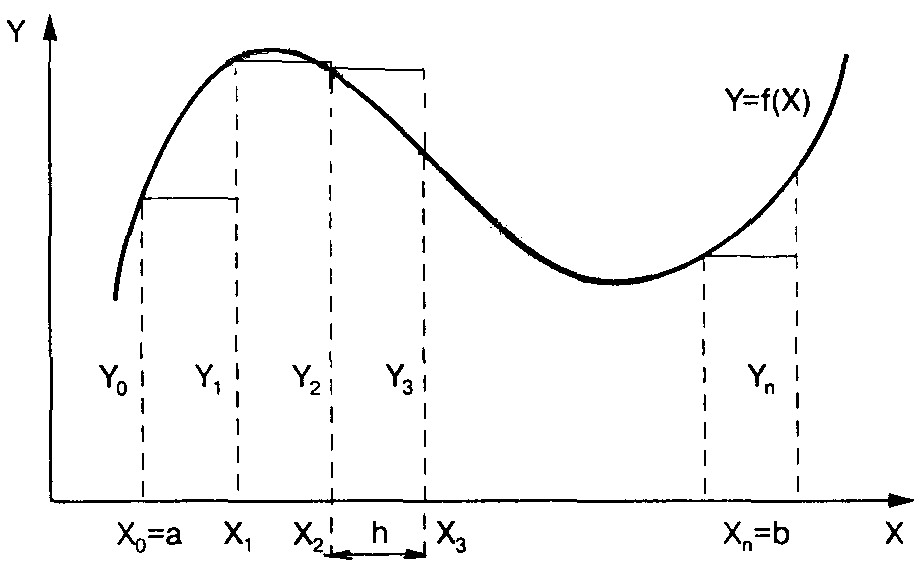 Рис.1. Геометрическая интерпретация интегрирования по методу прямоугольников. Площадь полученной ступенчатой фигуры можно найти как сумму площадей прямоугольников, стороны которых равны h и уi. Следовательно, площадь отдельного прямоугольника составит Si = yi∙h, тогда 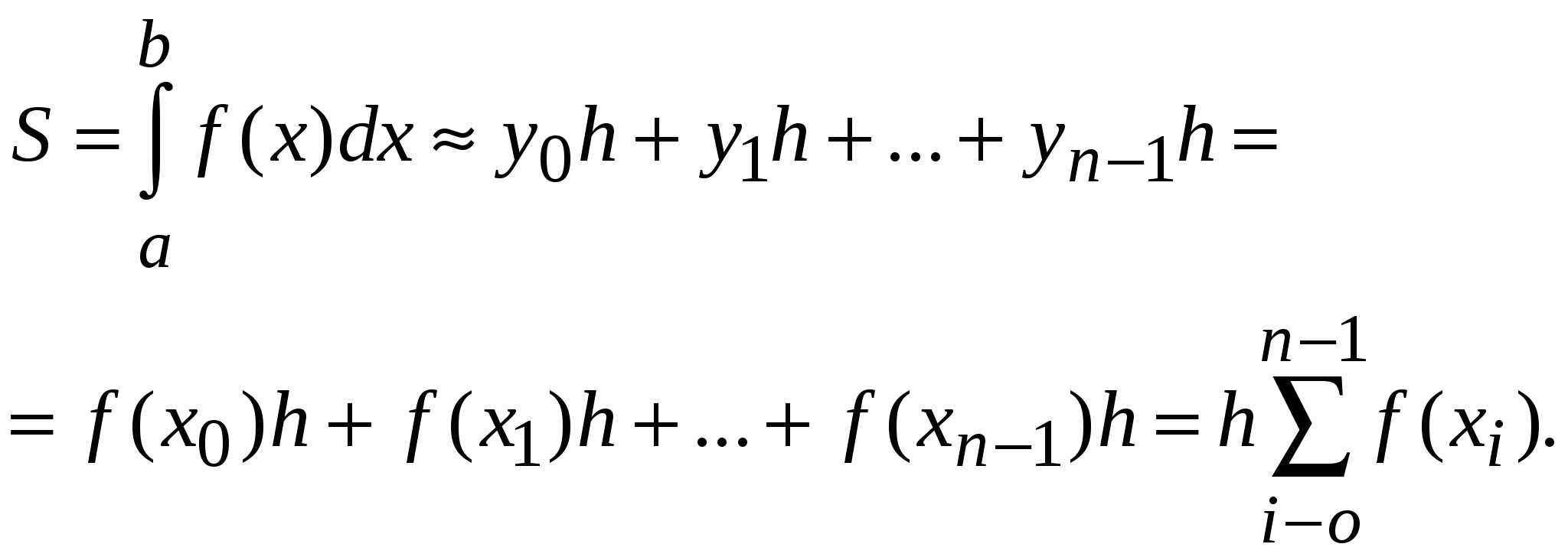 Следовательно, формула вычисления определённого интеграла по методу прямоугольников имеет вид:  (3)Остаточный член имеет вид:  (4)2) Интегрирование по методу трапеций. Метода трапеций заключается в линейной аппроксимации f(x) на отрезке [a,b]. Участок интегрирования также разбивается на n равных частей. Если провести ординаты во всех точках деления и заменить каждую из полученных криволинейных трапеций прямолинейной (рис.2), то приближённое значение интеграла будет равно сумме площадей прямолинейных трапеций. 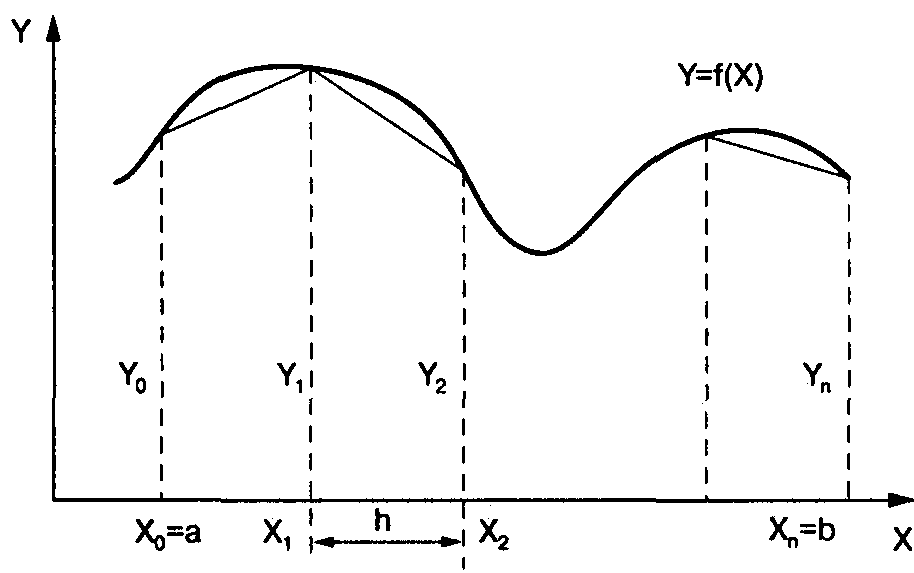 Рис. 2 Геометрическая интерпретация интегрирования по методу трапеций. Площадь отдельной трапеции составляет:  ,Тогда площадь искомой фигуры будем искать по формуле: 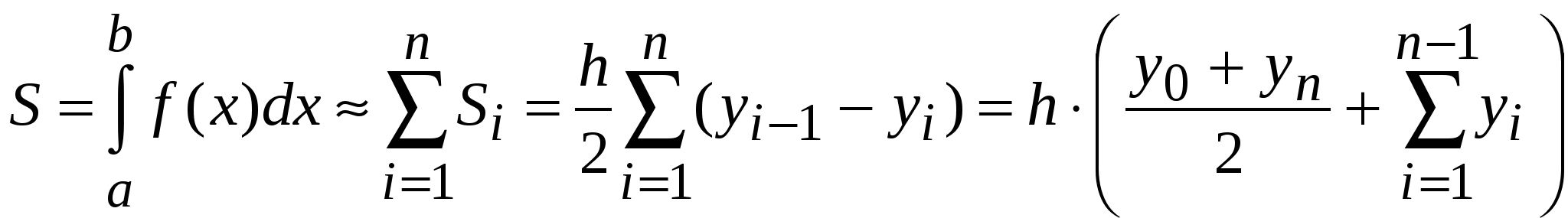 .Следовательно, формула трапеций для численного интегрирования имеет вид: 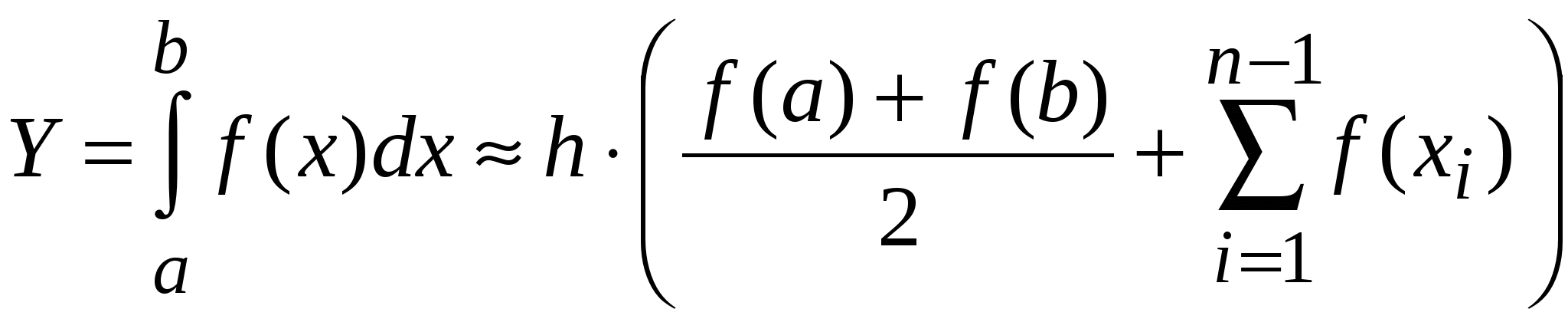 (5)Остаточный член имеет вид  (6)На практике для оценки абсолютной погрешности  формулы трапеций применяют следующие соотношения:1.  ,  (7)При этом, как правило, получают для завышенную оценку. 2. Правило Рунге (n − чётное) даёт более тонкую оценку : (8)Но при этом может получиться для заниженная оценка, чего следует опасаться. 3) Интегрирование по методу Симпсона. Пусть n = 2m − чётное число, а уi = f(xi) (i = 0..n) − значения функции у = f(x) для равноотстоящих точек a = x0, x1, x2, …, xn = b с шагом h =(b-a)/n = (b-a)/2m. На паре участков (рис.3) кривая у = f(x) заменяется параболой у = L(x), коэффициенты которой подобраны так, что она проходит через точки у0, у1, у2. 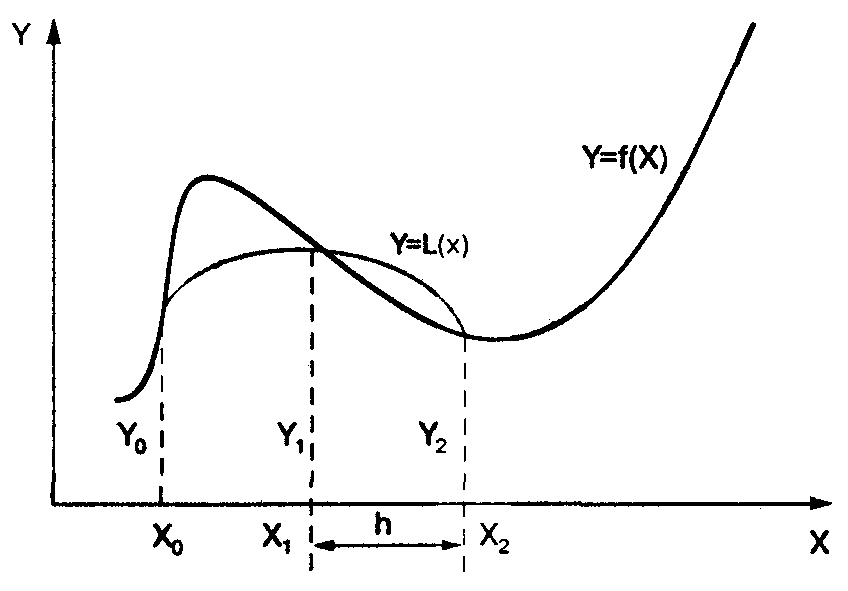 Рис.3 Геометрическая интерпретация интегрирования по методу Симпсона. Площадь криволинейной трапеции, ограниченной сверху параболой, составит:  .Суммируя площади всех криволинейных трапеций, получим: 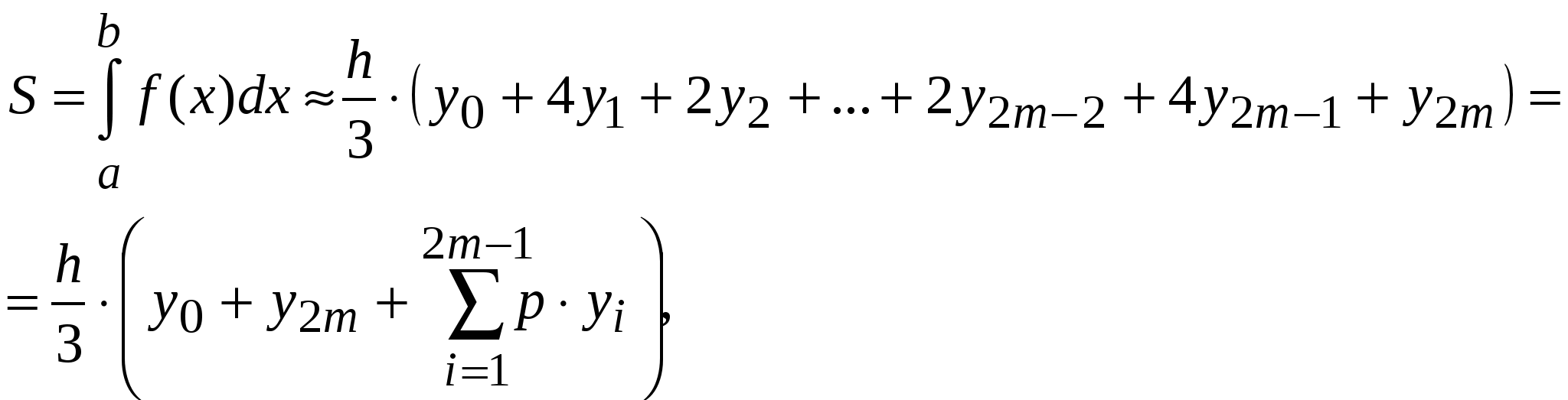 Где p = 6-p, p = 4. Следовательно, формула Симпсонадля численного интегрирования имеет вид: 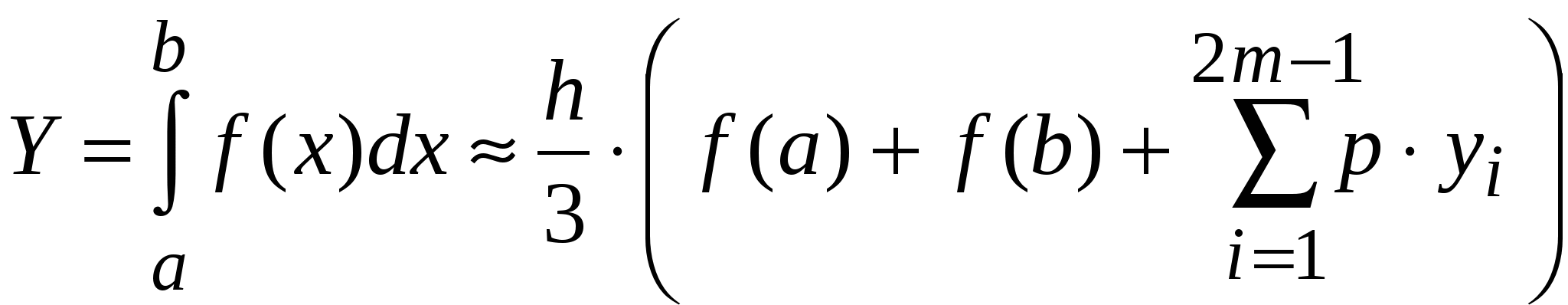 (9)Остаточный член имеет вид:  (10)На практике для оценки абсолютной погрешности  формулы Симпсона применяют следующие соотношения:1.  ,  (11)При этом, как правило, получают для  завышенную оценку. 2. Правило Рунге (n − чётное) даёт более тонкую оценку : (12)Но при этом может получиться для заниженная оценка, чего следует опасаться. Формулы прямоугольников и трапеций дают точное значение интеграла, когда подынтегральная функция f(x) линейна, ибо тогда f ″(x) = 0, а формула Симпсона является точной для многочленов до третьей степени, т. к. в этом случае f (4) = 0. Если функция у = f(x) задана таблично и её производные найти затруднительно, то в предполо- жении отсутствия быстро колеблющихся составляющих можно применить приближённые формулы для погрешностей, выраженные через конечные разности:  (*) (**)Выбор шага 1. Пусть требуется вычислить интеграл с точностью ε. Используя формулу соответствующего остаточного члена R, выбирают h таким образом, чтобы выполнялось неравенство  .2. Двойной пересчёт. ( Правило Рунге). Лекция 4 ЧИСЛЕННОЕ РЕШЕНИЕ ТРАНСЦЕНДЕНТНЫХ И НЕЛИНЕЙНЫХ УРАВНЕНИЙ. Если алгебраическое или трансцендентное уравнение достаточно сложное, то его корни сравнительно редко удаётся найти точно. Поэтому большое значение приобретают способы приближённого нахождения корней уравнения и оценки степени их точности. Процесс нахождения приближённых значений корней уравнения: f(x) = 0, (1) где функция f(x) определена и непрерывна в некотором конечном или бесконечном интервале a < x < b разбивается на два этапа: 1) отделение корней; 2) уточнение корней до заданной степени точности. |
,
.
