Лекции по кинематике. Лекция 10 Кинематика Вопросы Основные понятия
 Скачать 5.66 Mb. Скачать 5.66 Mb.
|
|
Ускорение точки при естественном способе задания движения Приведем некоторые сведения из дифференциальной геометрии, необходимые для определения ускорения при естественном способе задания движения. Пусть точка М движется по некоторой пространственной кривой. С каждой точкой этой кривой связаны три взаимно ортогональные направления (касательная, нормаль и бинормаль), однозначно характеризующие пространственную ориентацию бесконечно малого элемента кривой вблизи данной точки. Ниже приводится описание процесса определения указанных направлений. Для того чтобы провести касательную к кривой в точке М , проведем через нее и близлежащую точку М1 секущую ММ1. 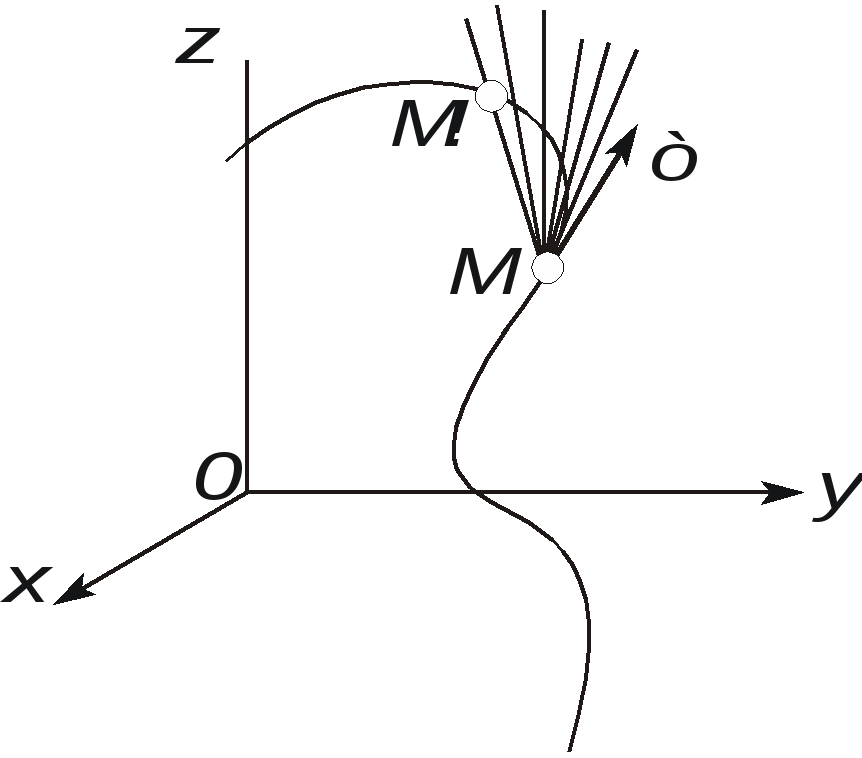 Рис. 2.10. Определение касательной к траектории движения точки Касательная к кривой в точке М определяется как предельное положение секущей ММ1 при стремлении точки М1 к точке М (рис. 2.10). Единичный вектор касательной принято обозначать греческой буквой Проведем единичные векторы касательных к траектории в точках М и М1. Перенесем вектор 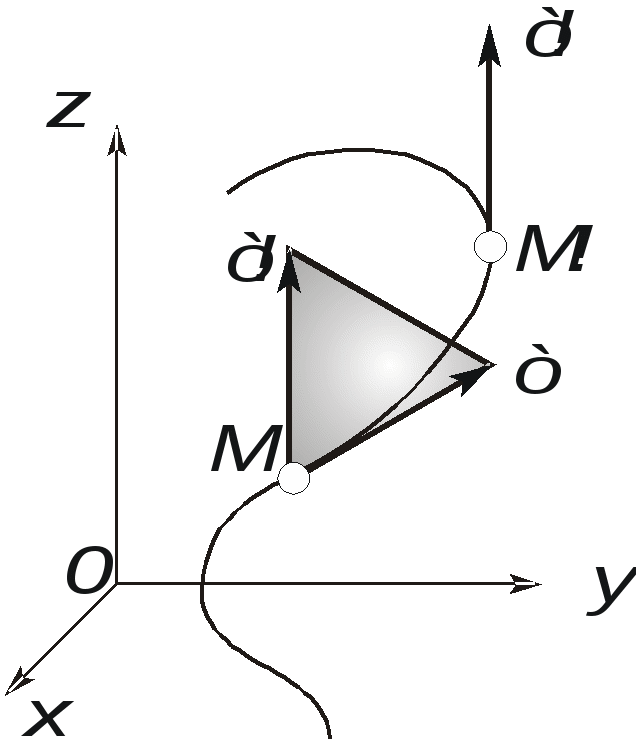 Рис. 2.11. Определение соприкасающейся плоскости Очевидно, что для плоской кривой соприкасающаяся плоскость совпадает с плоскостью, в которой лежит сама эта кривая. Плоскость, проходящая через точку М и перпендикулярная касательной в этой точке, называется нормальной плоскостью. Пересечение соприкасающейся и нормальной плоскостей образует прямую, называемую главной нормалью (рис. 2.12). 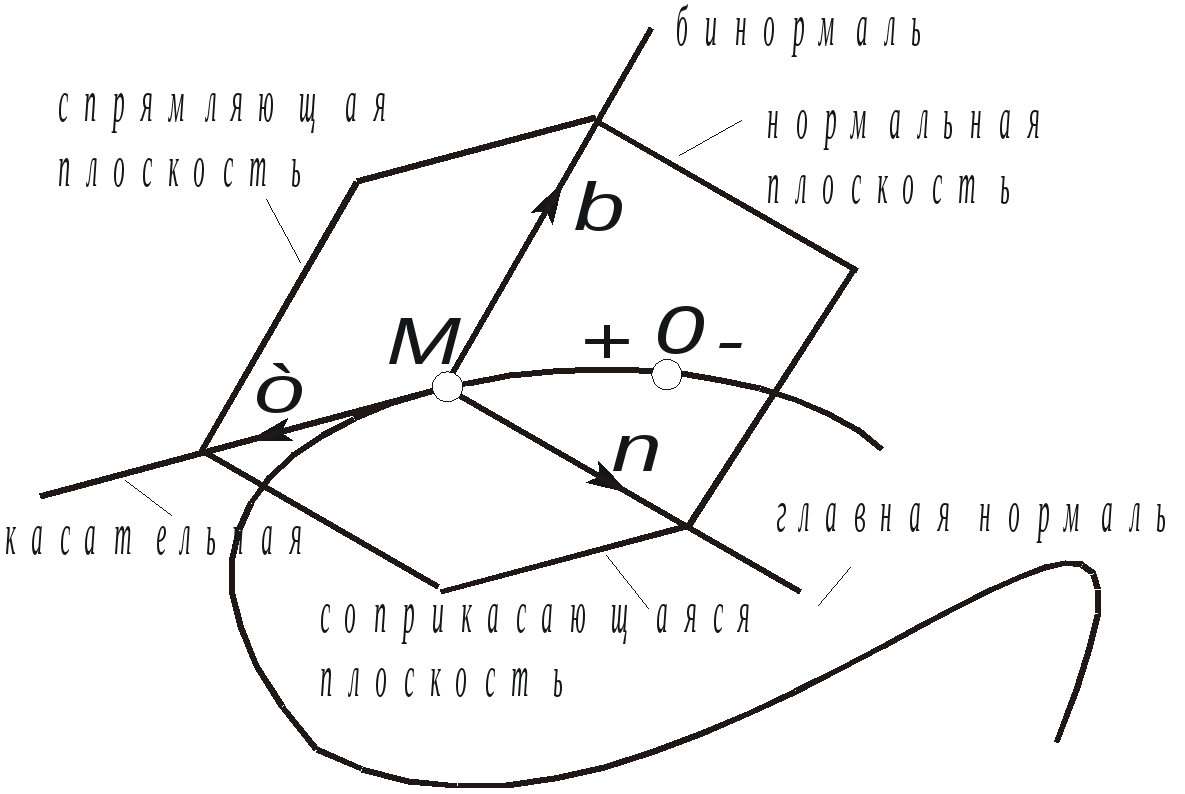 Рис. 2.12. Естественный трехгранник Единичный вектор, направленный вдоль главной нормали внутрь траектории, обозначим буквой Система координат, образуемая тремя взаимно ортогональными осями- касательной, нормалью и бинормалью, называется естественной системой координат. Трехгранник, образуемый соприкасающейся, нормальной и спрямляющей плоскостями называется естественным или подвижным трехгранником. Перемещаясь вместе с движущейся точкой М, оси этого подвижного трехгранника меняют свою ориентацию в пространстве, оставаясь взаимно ортогональными. Пример. Движение точки М задано уравнениями где k - постоянная. Определить модули скорости и ускорения как функции времени. Решение: Дважды дифференцируя уравнения движения по времени, получаем Подставляя найденные значения производных в формулы (8) и (14), получаем: Лекция 12 Вопросы 1. Ускорение точки (продолжение) 2. Частные случаи движения точки 1. Ускорение характеризует не только изменение величины скорости, но и изменение ее направления. Очевидно, что быстрота изменения направления вектора скорости, при прочих равных условиях, зависит от степени искривленности траектории. Для количественной оценки этой искривленности вводится понятие кривизны. Пусть вектор скорости 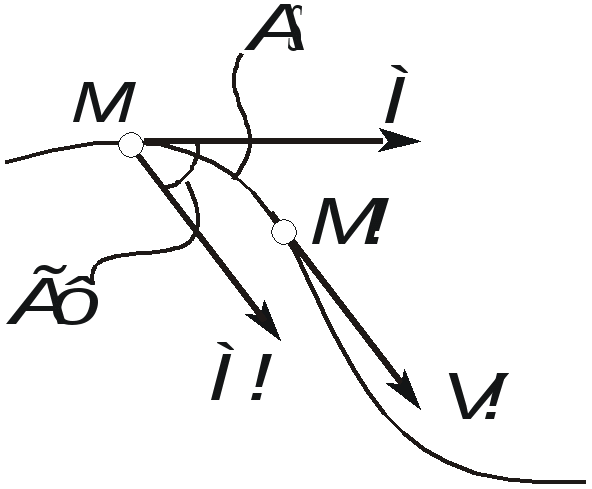 Рис. 2.13. Определение кривизны кривой Средней кривизной на этом участке траектории называется отношение kср = /S. Предел этого отношения при 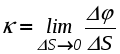 . (2.15) . (2.15) Вычислим производную единичного вектора 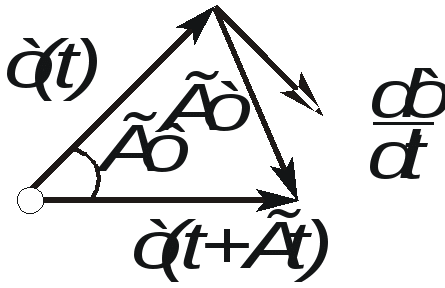 Рис. 2.14. К определению величины и направления вектора dт/dt 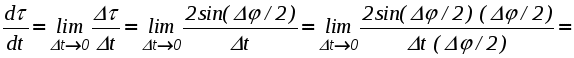 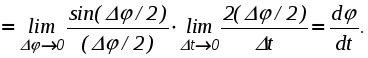 Из рис. 2.14 видно, что при стремлении t к нулю, углы при основании треугольника стремятся к прямым углам и, следовательно, вектор 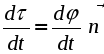 . (2.17) . (2.17) Перейдем к выводу формул, определяющих ускорение точки при естественном способе задания движения. Согласно (2.10) и (2.11), имеем: 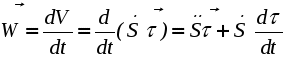 . (2.18) . (2.18) Первое слагаемое в правой части (2.18) направлено по касательной к траектории и называется касательной составляющей полного ускорения: 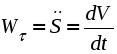 . (2.19) . (2.19) Если 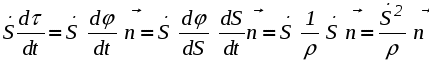 , ,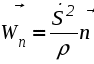 , , 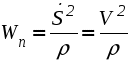 . (2.20) . (2.20) Итак, ускорение при естественном способе задания движения определяется как геометрическая сумма (рис. 2.15) его касательной и нормальной составляющих: 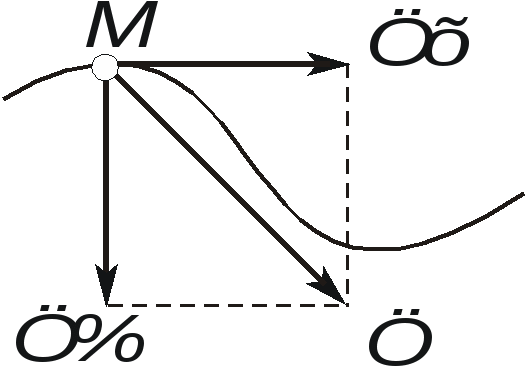 Рис. 2.15. Определение полного ускорения точки Касательное ускорение характеризует изменение скорости по величине, нормальное ускорение - по направлению. Отметим случаи, когда равны нулю отдельные составляющие ускорения. Касательное ускорение W = dV/dt равно нулю при равномерном движении ( V = const) и в точках траектории, где величина скорости достигает своего минимального или максимального значения (dV/dt)=0. Нормальное ускорение Wn = V2/ равно нулю при прямолинейном движении и в точках перегиба траектории (когда 2. Частные случаи движения точки Все выведенные выше формулы справедливы для любого движения точки. Рассмотрим теперь два важных частных случая - равномерное и равнопеременное движение. Равномерным называется движение точки с постоянной по величине скоростью, т.е. когда V = const. Выведем уравнение равномерного движения. Согласно (2.10) V = dS/dt или dS = Vdt. Интегрируя последнее выражение и учитывая, что V = const, получаем закон равномерного движения: 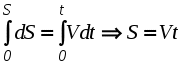 . (2.22) . (2.22) Равнопеременным (равноускоренным или равнозамедленным) называется движение с постоянным по величине касательным ускорением (W= const). Получим формулы для такого движения. Имеем: 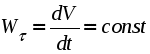 , , 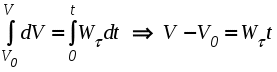 , ,Подставляя вместо V = dS/dtи интегрируя полученное выражение, находим закон или уравнение равнопеременного движения: 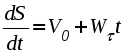 , , 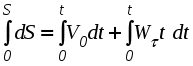 , ,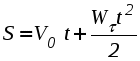 . (2.24) . (2.24) Пример. Точка движется по окружности радиуса R равноускоренно из состояния покоя и совершает первый полный оборот за T секунд. Определить модули скорости и ускорения точки в конце этого промежутка времени. Решение. Так как по условию задачи движение точки равноускоренное, воспользуемся формулой (2.24) для определения касательного ускорения точки: 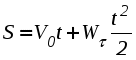 . .Подставляя S = 2R, t = T и V0 = 0 , определяем W: 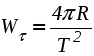 . .Зная W, определяем скорость точки в момент времени T по формуле (2.23): 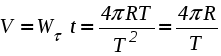 . .Нормальное ускорение точки в момент времени T будет равно 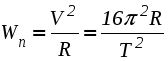 . . Полное ускорение точки определяем по формулу (2.21): 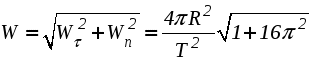 . .Лекция 13 Вопросы 1. Поступательное движение твердого тела и его свойства. 2. Вращательное движение твердого тела. 3. Частные случаи вращательного движения.
В кинематике твердого тела, к изложению которой мы приступаем, решаются те же, что и в кинематике точки, две основные задачи: - задание движения твердого тела; - определение основных кинематических характеристик этого движения. Решение первой задачи сводится к определению необходимого числа функций времени (уравнений движения), однозначно определяющих положение каждой точки тела в пространстве. Решение второй задачи заключается в определении зависимостей, позволяющих по известным уравнениям движения определить траекторию, а также скорость и ускорение любой точки тела в любой момент времени. Различают пять видов движения твердого тела: поступательное, вращательное, плоскопараллельное, сферическое и свободное. Первые два из них (поступательное и вращательное) называют простейшими.
Поступательным называется такое движение тела, при котором любая прямая, соединяющая две произвольные точки тела, перемещается, оставаясь параллельной своему начальному направлению. Поступательное движение может быть как прямолинейным, так и криволинейным (рис.2.16). 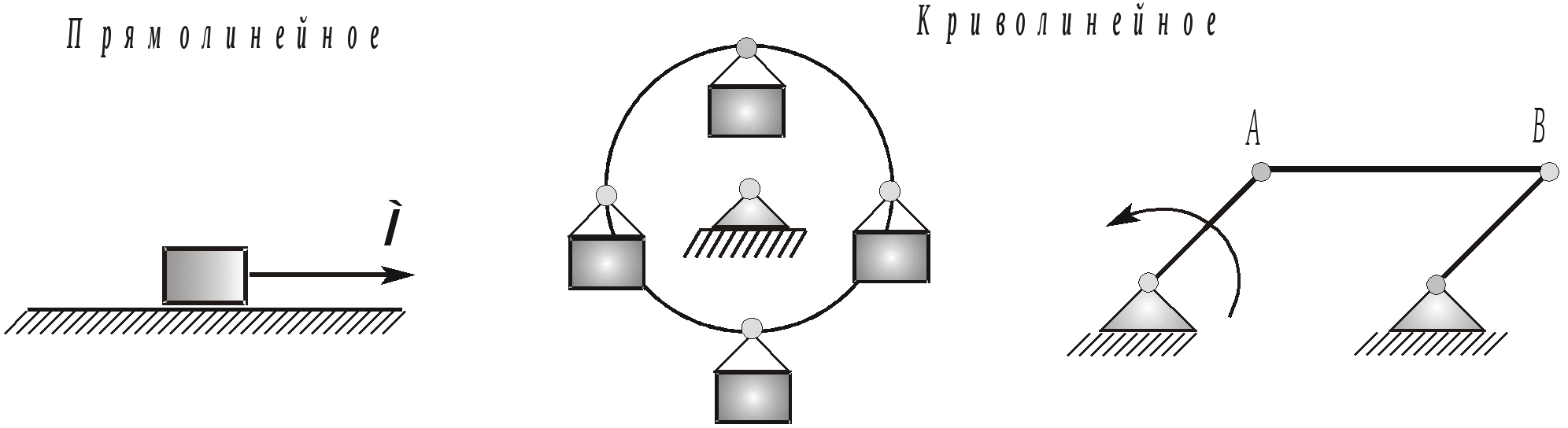 Рис. 2.16. Примеры поступательного движения твердого тела Докажем следующие свойства поступательного движения. Если тело движется поступательно, то все его точки в каждый момент времени имеют одинаковые скорости и ускорения, а траектории всех точек при наложении совпадают. Пусть тело движется поступательно. Тогда (см. рис.2.17) для любых двух его точек А и В, в любой момент времени справедливо следующее векторное выражение: где вектор 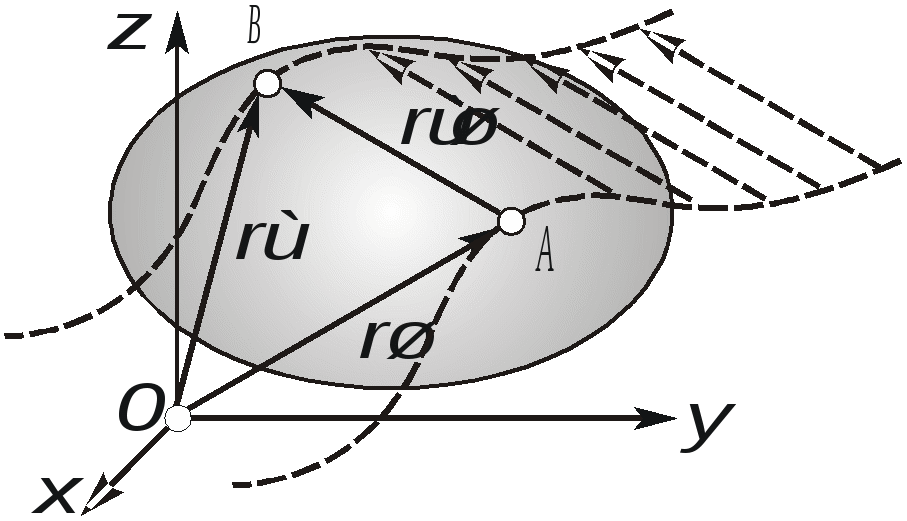 Рис. 2.17. К определению свойств поступательного движения Дифференцируя вышеприведенное векторное выражение по времени, получаем: 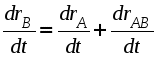 , или , или так как последняя производная (как производная от постоянного вектора Доказанные свойства позволяют свести изучение поступательного движения тела к изучению движения любой одной из его точек методами кинематики точки.
Движение твердого тела, при котором все точки, лежащие на некоторой прямой, принадлежащей телу или неизменно с ним связанной, остаются неподвижными в рассматриваемой системе отсчета, называется вращательным движением. Упомянутая выше прямая называется осью вращения. 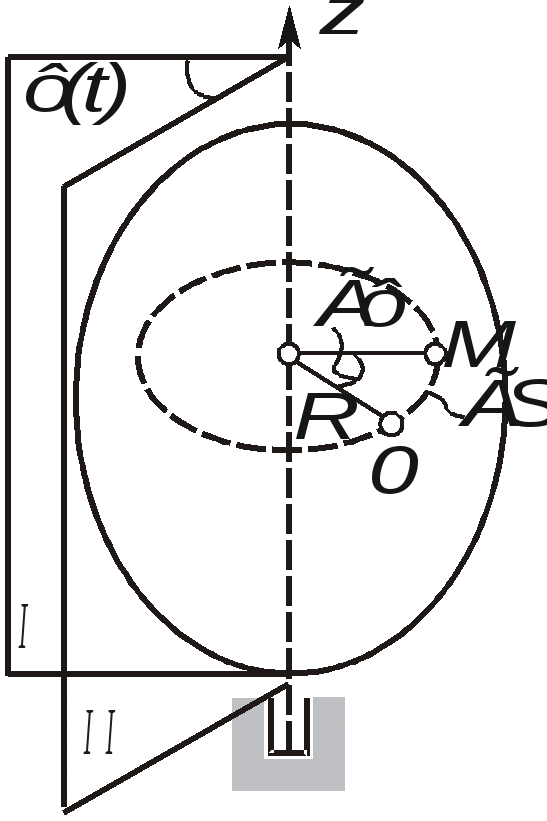 Рис. 2.18. Вращение тела вокруг неподвижной оси Очевидно, что все точки тела, не лежащие на оси вращения, будут двигаться по окружностям, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси. Положение тела при вращательном движении можно однозначно определить углом между неподвижной полуплоскостью I и подвижной, вращающейся вместе с телом, полуплоскостью II, проходящими через ось вращения. Положительным направлением отсчета угла называемого также угловой координатой, принято считать вращение против хода часовой стрелки, если смотреть навстречу оси вращения z . Сам угол принято измерять в радианах. Для однозначного определения положения тела в любой момент времени, необходимо располагать зависимостью угловой координаты от времени: = (t) . (2.25) Уравнение (2.25) называется уравнением или законом вращательного движения твердого тела. Введем основные кинематические характеристики вращательного движения - угловую скорость и угловое ускорение . Пусть за промежуток времени t тело повернется на угол. Тогда отношение t называют средней угловой скоростью за этот промежуток времени: ср = t. Предел данного отношения при стремлении t к нулю, называют мгновенной или просто угловой скоростью: 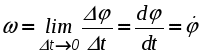 . (2.26) . (2.26)Аналогичным образом вводится понятие углового ускорения: 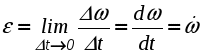 . (2.27) . (2.27) Согласно (2.26) и (2.27) угловая скорость и угловое ускорение измеряются в радианах в секунду (рад/с) и в радианах в секунду за секунду (рад/с2) соответственно. Так как радиан является безразмерной величиной, допустимы и более компактные обозначения - (с -1) и (с -2). Для того, чтобы использовать угловую скорость и угловое ускорение в векторных выражениях, необходимо рассматривать угловую скорость как вектор, с модулем равным d/dt и направленным вдоль оси вращения в ту сторону, откуда вращения тела видно происходящим против хода часовой стрелки. Вектор углового ускорения, модуль которого равен d/dt, также считают направленным вдоль оси вращения. Он совпадает по направлению с вектором угловой скорости при ускоренном вращении и противоположен ему при замедленном вращении тела (рис. 2.19). Необходимо отметить, что введенные таким необычным способом векторы называют псевдовекторами ( как бы векторами), чтобы подчеркнуть их некоторую “векторную неполноценность”. Тем не менее теперь становится возможна запись следующей векторной формулы: правильно отражающей не только количественную связь 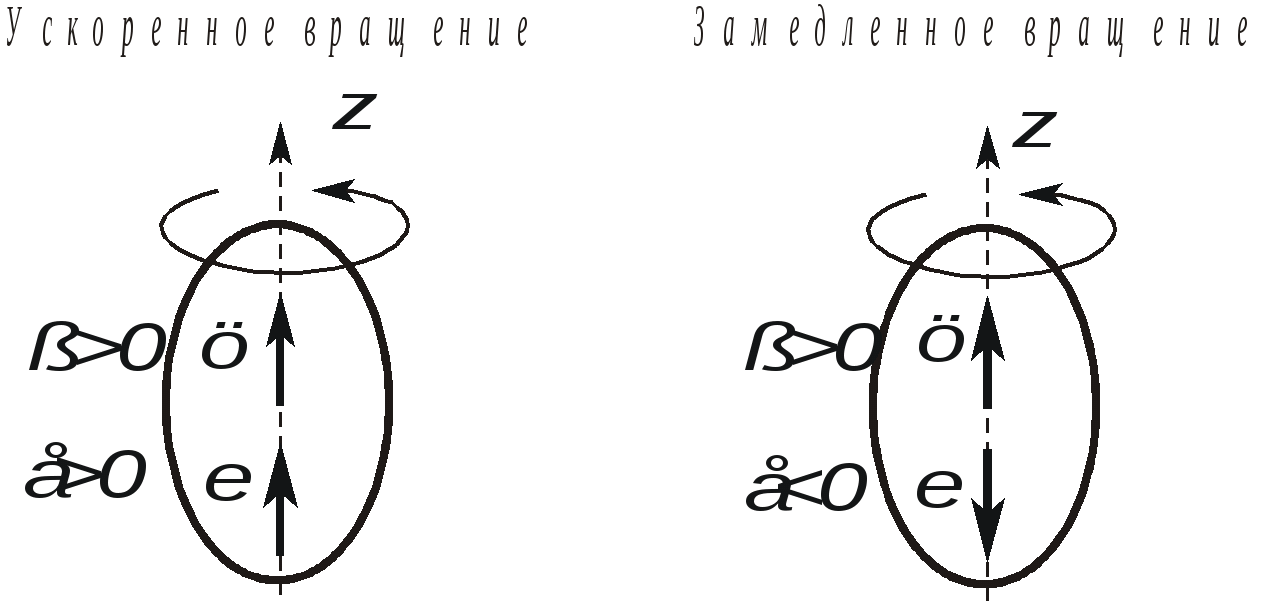 Рис. 2.19. Взаимосвязь направлений циe Перейдем теперь к определению индивидуальных кинематических характеристик точек вращающегося тела по известному закону вращательного движения  Рис. 2.20. Связь угловой скорости тела с линейными скоростями его точек Тогда ее скорость будет равна 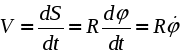 , т.е. , т.е. Так как всех точки тела вращаются с одной и той же угловой скоростью, то из (2.29) следует, что линейные скорости точек тела пропорциональны их расстояниям от оси вращения. Для определения ускорений воспользуемся формулами (2.19) и (2.20): 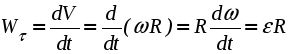 , (2.30) , (2.30)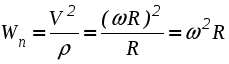 . (2.31) . (2.31) Полное ускорение точки М будет равно (рис. 2.21) геометрической сумме 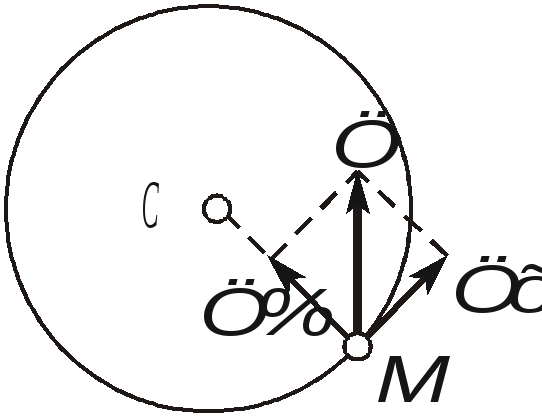 Рис. 2.21. Ускорение точек тела при вращательном движении
а) Равномерное вращение - вращение с постоянной угловой скоростью ( = const): 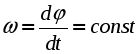 , , Пусть при t = 0: = 0, тогда С = 0 и мы получаем следующее уравнение или закон равномерного вращения: в) Равнопеременное вращение - это вращение с постоянным угловым ускорением ( = const): 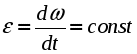 , , 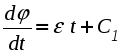 , , 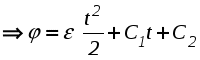 . .Пусть при t = 0: и = 0, тогда С1 = , C2 = 0. Подставляя найденные значения констант интегрирования в полученные выше выражения, получаем: В полученном законе изменения угловой скорости (2.34) и в уравнении равнопеременного вращения (2.35), угловое ускорение будет положительным при равноускоренном вращении и отрицательным при равнозамедленным. В заключение приведем вполне очевидные соотношения, которые часто используются при решении задач: 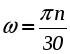 (2.36) (2.36)где N - число оборотов, n - угловая скорость в оборотах в минуту. 4. Формула Эйлера В заключение получим векторные формулы для скорости и ускорения точек в круговом движении. Рассмотри движение точки М, не лежащей на оси вращения (рис. 2.22). Покажем, что ее скорость полностью определяется формулой Эйлера : 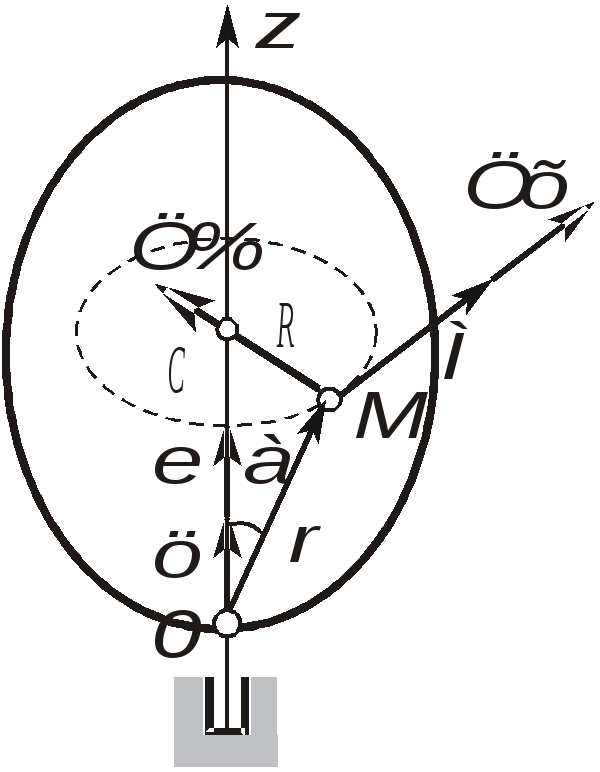 Рис. 2.22. Иллюстрация формулы Эйлера Действительно, модуль векторного произведения Для вывода векторных формул, определяющих ускорение, продифференцируем формулу Эйлера по времени: 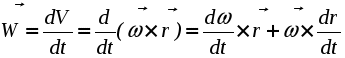 . .Учитывая, что согласно (2.28) и (2.5) 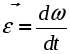 , , 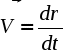 получаем: где В справедливости выражений (2.36) можно убедиться непосредственно, определив модули и направления входящих в них векторных произведений. Так согласно первой формуле (2.39) Лекция 14 Вопросы 1. Плоскопараллельное движение твердого тела. 2. Скорости точек при плоскопараллельном движении.
1. Плоскопараллельным (или плоским) называется такое движение твердого тела , при котором все его точки движутся параллельно некоторой неподвижной плоскости (рис. 2.23). Частным случаем плоскопараллельного движения является вращательное движение тела. 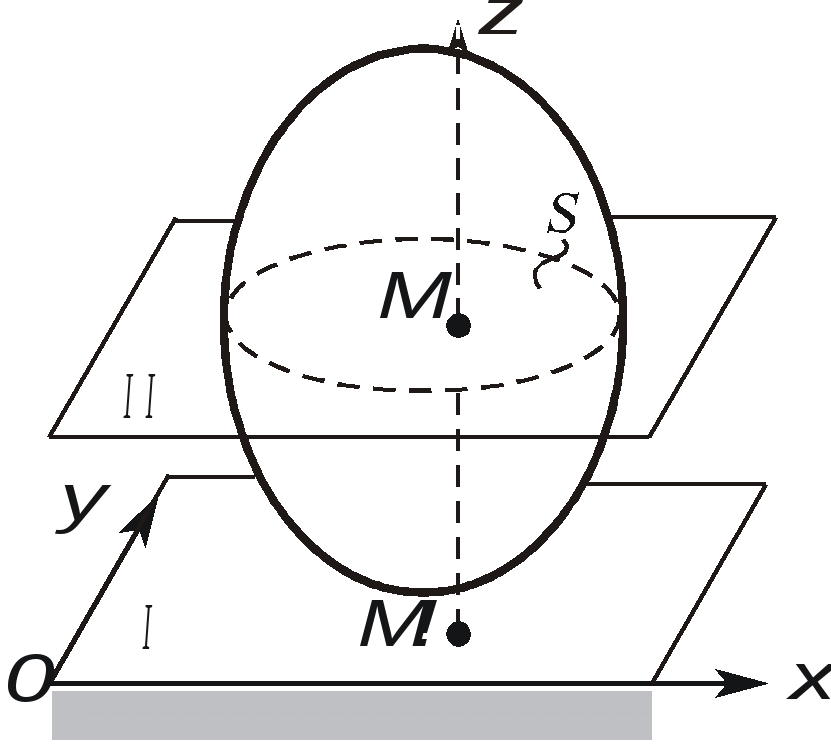 Рис. 2.23. Плоскопараллельного движения тела Согласно определению плоскопараллельного движения, любая прямая, неизменно связанная с телом и перпендикулярная неподвижной плоскости I, движется поступательно. Это означает, что все точки этой прямой движутся одинаково (см. свойства поступательного движения). Поэтому вместо того, чтобы изучать движение всех точек объемного тела, достаточно изучить движение точек плоской фигуры S (полученной сечением тела плоскостью ІІ, параллельной плоскости І) (рис. 2.24). Положение плоской фигуры S в плоскости XOY (которую мы для удобства расположим в плоскости листа), однозначно определяется произвольно проведенным на этой фигуре отрезком АВ (рис. 2.24). В свою очередь, положение отрезка АВ можно определить, зная координаты точки А и угол , который данный отрезок составляет c осью x.  Рис. 2.24. Определение положения фигуры S в плоскости x0y Таким образом, для определения положение плоской фигуры S (а, следовательно, и всего объемного тела) в любой момент времени необходимо знать зависимости: Уравнения (2.40) называются уравнениями плоскопараллельного движения твердого тела. Произвольная точка А , выбранная для определения положения плоской фигуры, называется полюсом. Первые два из уравнений (2.40) определяют поступательное движение фигуры S, при котором все ее точки движутся так же как полюс А (см. свойства поступательного движения). Очевидно, что вид этих уравнений будут зависеть от выбора полюса. Вид третьего уравнения, описывающего вращательную часть движения плоской фигуры S, а также ее угловая скорость и угловое ускорение , от выбора полюса не зависят. Как и при вращательном движении, угловую скорость и угловое ускорение можно рассматривать как псевдовекторы 2. Скорости точек при плоском движении Для определения скоростей при плоскопараллельном движении используются: формула распределения скоростей, теорема о проекциях и понятие мгновенного центра скоростей (МЦС). а) Формула распределения скоростей 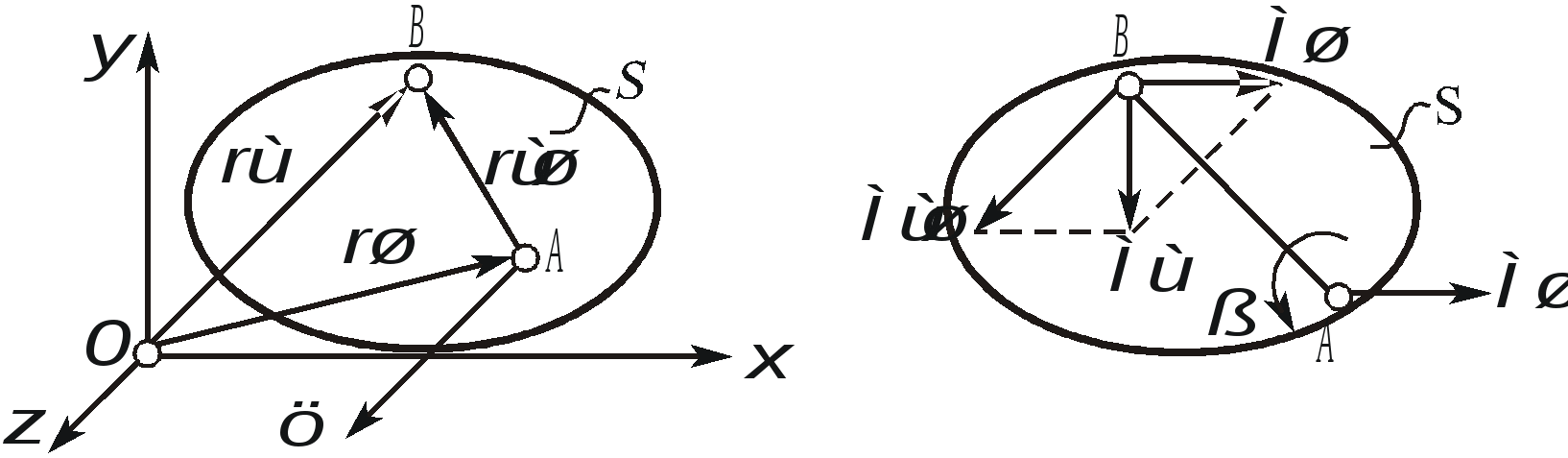 Рис. 2.25. К выводу формулы распределения скоростей Из рис. 2.25 видно, что положение произвольной точки В плоской фигуры S в каждый момент времени определяется следующим векторным равенством: Продифференцируем данное выражение по времени 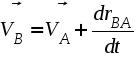 , ,согласно формуле Эйлера (2.38) 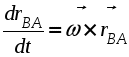 , ,Обозначая Согласно (41), скорость произвольной точки В плоской фигуры равна геометрической сумме скорости полюса б) Теорема о проекциях: при любом движении твердого тела проекции скоростей любых двух его точек на прямую, соединяющую эти точки, равны между собой (рис. 2.26). 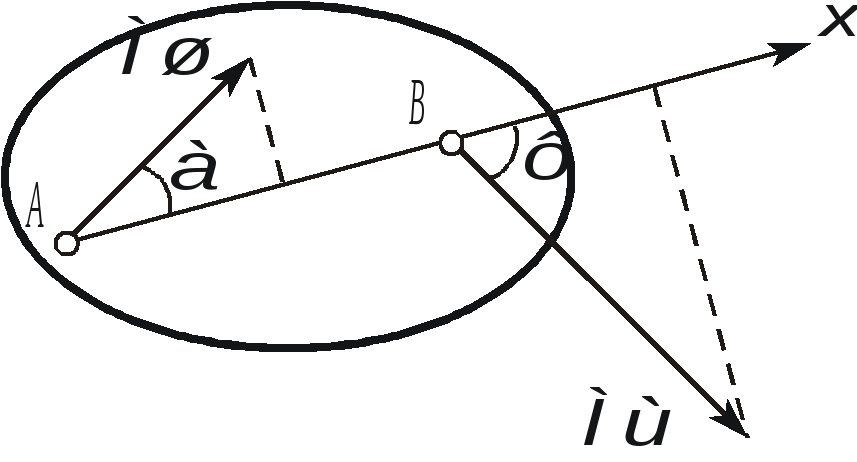 Рис. 2.26. К теореме о проекциях Спроецируем на ось x, проходящую через точки А и В формулу (2.41). Так как что и требовалось доказать. в) Использование понятия мгновенного центра скоростей. Определение: мгновенным центром скоростей (МЦС) называется точка плоской фигуры, скорость которой в данный момент времени равна нулю. МЦС принято обозначать буквой Р. Покажем, что если плоская фигура не движется поступательно, то такая точка существует в каждый момент времени. Для этого восстановим перпендикуляры к скоростям двух произвольных точек А и В и найдем точку их пересечения (рис. 2.27). 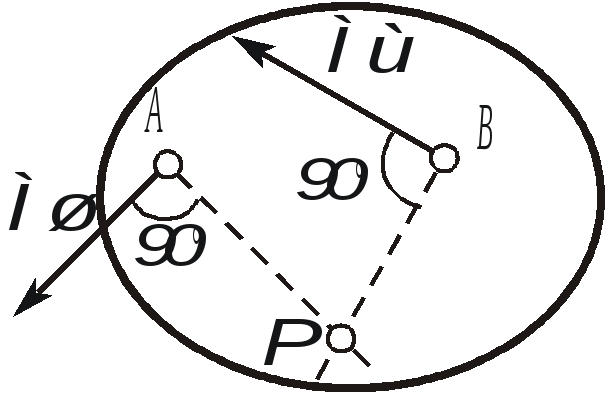 Рис. 2.28. Основной случай определения положения М.Ц.С. Покажем, что скорость точки Р равна нулю и, следовательно, эта точка по определению является мгновенным центром скоростей. Согласно (2.41) имеем Поскольку векторы Если теперь взять за полюс точку Р, то для точек А и В формула (2.41) запишется в виде: Учитывая, что Из (2.42) следует, что скорости точек плоской фигуры пропорциональны их расстояниям от мгновенного центра скоростей и движение плоской фигуры можно рассматривать как вращение вокруг меняющего свое положение мгновенного центра скоростей. Мгновенную угловую скорость этого вращения можно найти, поделив скорость любой точки на ее расстояние от мгновенного центра скоростей. Кроме основного случая нахождения положения МЦС, рассмотренного выше, при решении задач встречаются следующие варианты:  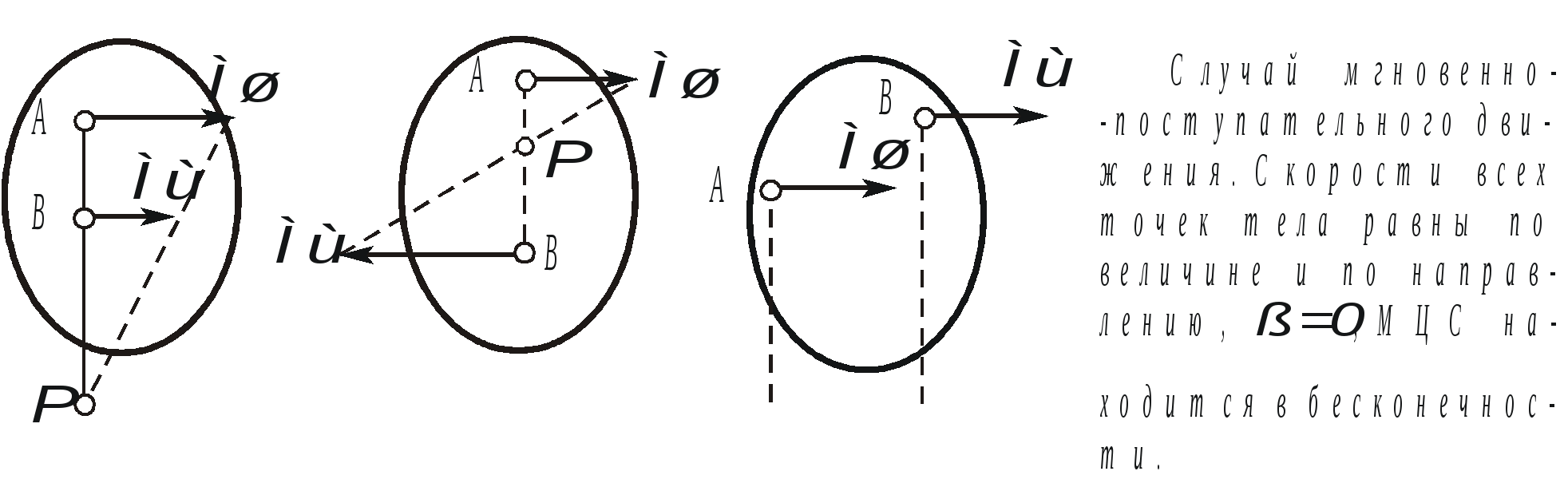  Рис. 2.28. Частные случаи определения положения МЦС 3. Ускорения точек в плоском движении. Формула распределения ускорений. Для вывода данной формулы распределения ускорений запишем выражение (2.41) в виде: и, продифференцировав его по времени, получим: 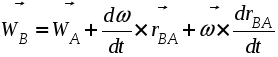 . . Учитывая, что 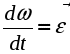 , а по формуле Эйлера , а по формуле Эйлера 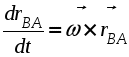 , имеем: , имеем: Введем следующие обозначения: Векторы По определению векторного произведения вектор получаем поскольку 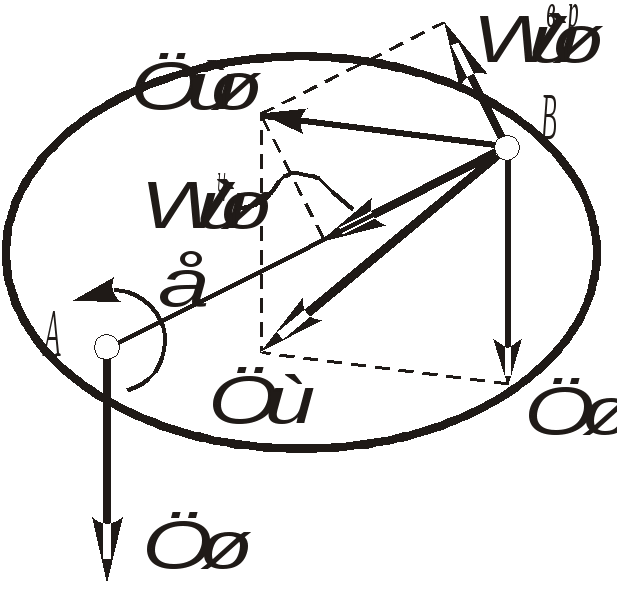 Рис. 2.29. Иллюстрация формулы распределения ускорений Окончательно формулу распределения ускорений можно записать в виде: в которой Формулу (2.43) иногда используют в виде где вектор 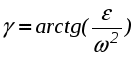 к отрезку АВ и равен по модулю к отрезку АВ и равен по модулю Пример 1. Найти ускорение точки В, угловое ускорение шатуна АВ и угловое ускорение кривошипа ВС четырехзвенного механизма в положении, указанном на рис. 2.29. Кривошип ОА вращается равномерно с угловой скоростью 0 = 5 c-1 , длина шатуна АВ равна 0,8 м. 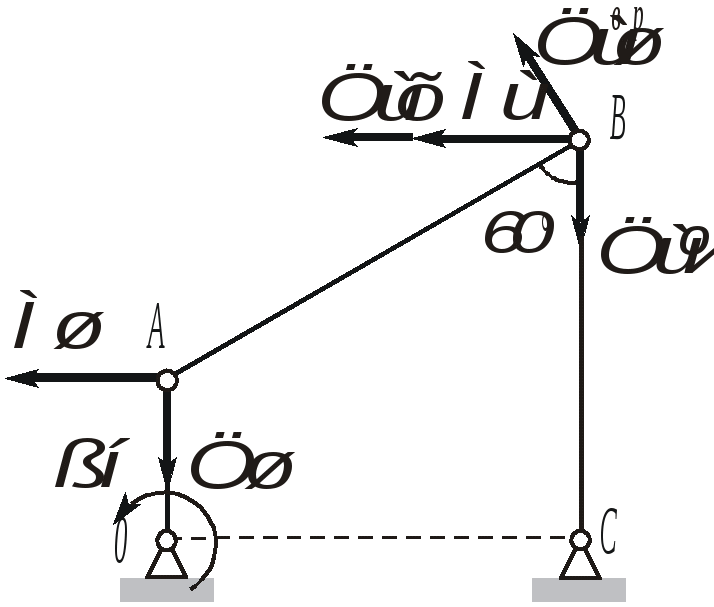 Рис. 2.29. Пример использования формулы распределения ускорений Решение. Определим скорость и ускорение точки А, которую затем выберем в качестве полюса: VA = OA = 2 м/с, WA = OA = 10 м/сек2. Так как М.Ц.С. звена АВ находится в бесконечности (Мщ параллелен Мш), AB = 0. Ускорение точки В, как точки, принадлежащей звену АВ, по формуле распределения ускорений равно: С другой стороны, ускорение точки В , как точки принадлежащей звену ВС и вращающейся вокруг точки С, можно представить в виде сумму ее касательного и нормального ускорений: 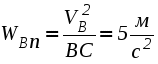 , , Приравнивая правые части выражений для Проектируя (*) на направления отрезков ВС и АВ имеем : откуда 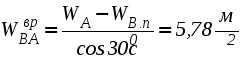 , , 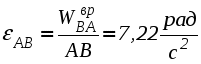 , ,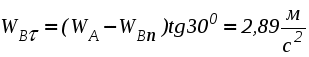 , , 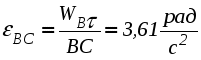 . .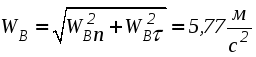 . .
Мгновенным центром ускорений называется точка плоской фигуры, ускорение которой в данный момент времени равно нулю. М.Ц.У принято обозначать буквой Q. Покажем, что если плоская фигура (рис. 2.30) не движется поступательно, то такая точка существует в каждый момент времени и ее положение легко определить (зная ускорение какой-либо точки из выражения 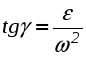 определим угол ; определим угол ;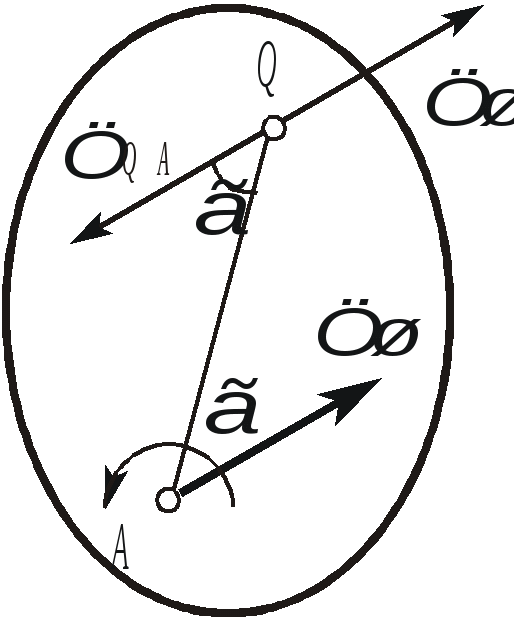 |
