Лекции по кинематике. Лекция 10 Кинематика Вопросы Основные понятия
 Скачать 5.66 Mb. Скачать 5.66 Mb.
|
|
Рис. 2.30. К определению положения мгновенного центра ускорений от точки А под углом к вектору Найденная таким образом точка Q и будет являться мгновенным центром ускорений. Действительно, по формуле распределения ускорений, имеем Подставляя сюда AQ из (2.44), находим, что WQA = WA. Кроме того, вектор Следовательно, ускорения точек плоской фигуры определяются в каждый данный момент времени так, как если бы движение плоской фигуры было вращением вокруг мгновенного центра ускорений Q (рис. 2.31). При этом ускорения точек плоской фигуры будут пропорциональны их расстояниям от М.Ц.У. 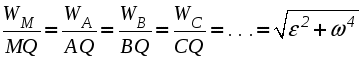 . . 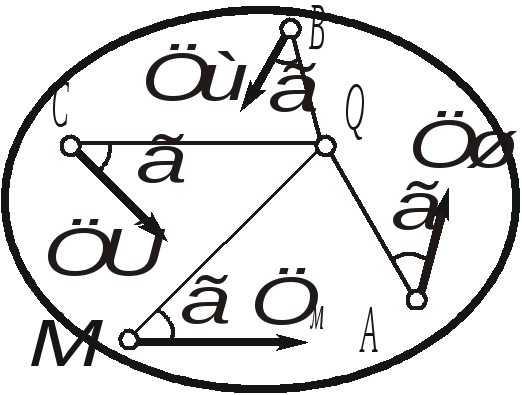 Рис. 2.31. Определение ускорений с помощью М.Ц.У. 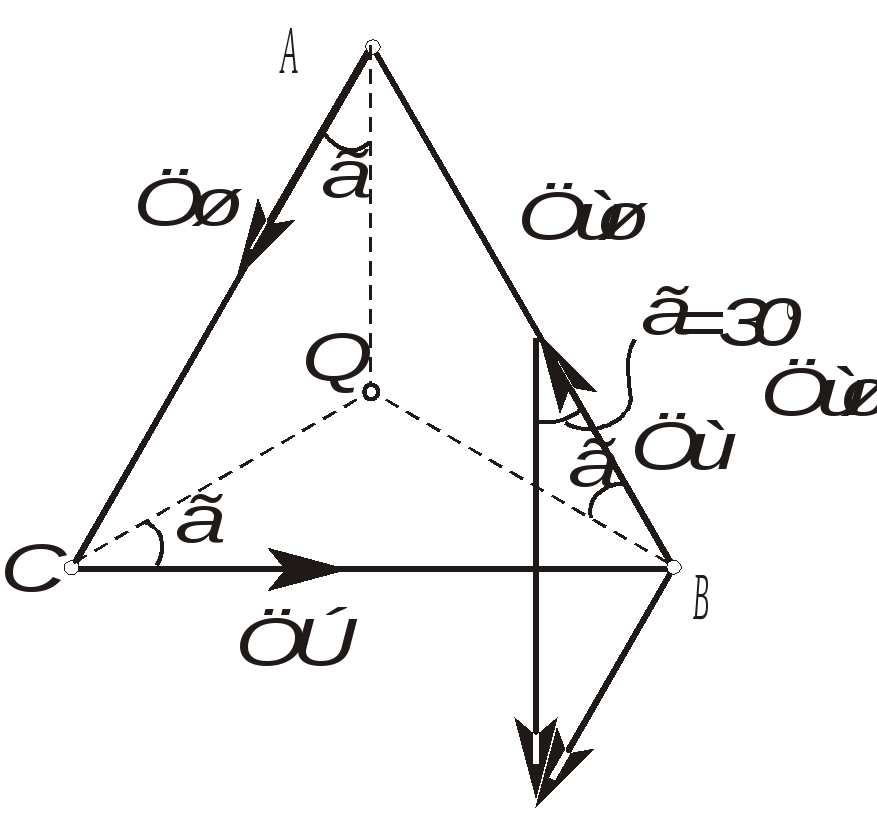 Пример 2. Равносторонний треугольник АВС движется в плоскости чертежа. Ускорения вершин А и В равны в данный момент времени 16 см/с2 и направлены по сторонам треугольника. Определить ускорение третьей вершины С треугольника. Решение. Определим ускорение точки С используя понятие мгновенного центра ускорений. Для определения его положения необходимо знать угол между вектором Цщш и отрезком АВ. (см. рис 2.30). Очевидно, что в нашем случае этот угол равен 30º. Положение мгновенного центра ускорений Q определим как точку пересечения двух прямых, проведенных под углом к векторам Цш и Цщ. Так как расстояния вершин треугольника от точки Q одинаковы, ЦЪ=16 см/с2 . Направление этого вектора показано на рисунке. Лекция 15 1. Сложное движение точки. 2. Определение скоростей и ускорений точки в сложном движении. 1. Во многих задачах механики удобно считать, что движение точки относительно основной (условно неподвижной) системы отсчета состоит из нескольких более простых движений. Для этого вводят в рассмотрение вторую (подвижную) систему отсчета, движущуюся относительно основной. Теперь движение точки относительно неподвижной системы можно рассматривать как сумму одновременно происходящих двух движений: движения относительно подвижной системы отсчета и движения точки вместе с подвижной системой относительно неподвижной. Так, например, можно считать, что движение человека, идущего по эскалатору метро, по отношению к неподвижной стене туннеля (относительно неподвижной системы отсчета) состоит из двух движений, а именно из движения человека относительно движущегося эскалатора (относительно подвижной системы координат) и его движения вместе с эскалатором относительно неподвижной стены. Аналогичным образом могут быть представлены движения человека, плывущего по реке, по отношению к неподвижному берегу, движение поднимаемого мостовым краном груза при одновременном перемещении кран балки, движение снаряда в канале ствола зенитного орудия при одновременном вращении ствола в процессе слежения за целью и т.п. Такое движение точки, рассматриваемое одновременно в неподвижной и в подвижной системах отсчета, называется сложным или составным. При этом движение точки относительно основной (неподвижной) системы отсчета называется абсолютным. Скорость и ускорение точки в этом движении называется абсолютной скоростью и абсолютным ускорением и обозначаются Движение подвижной системы отсчета относительно неподвижной называется переносным движением. Скорость и ускорение той, неизменно связанной с подвижной системой отсчета точки пространства, с которой в данный момент времени совпадает движущаяся точка, называется переносной скоростью 2. Пусть в некоторый момент времени t точка М занимает положение, указанное на рисунке 2.32. Ее относительная траектория - кривая АВ , неизменно связанная с подвижной системой координат (на рисунке не показана). 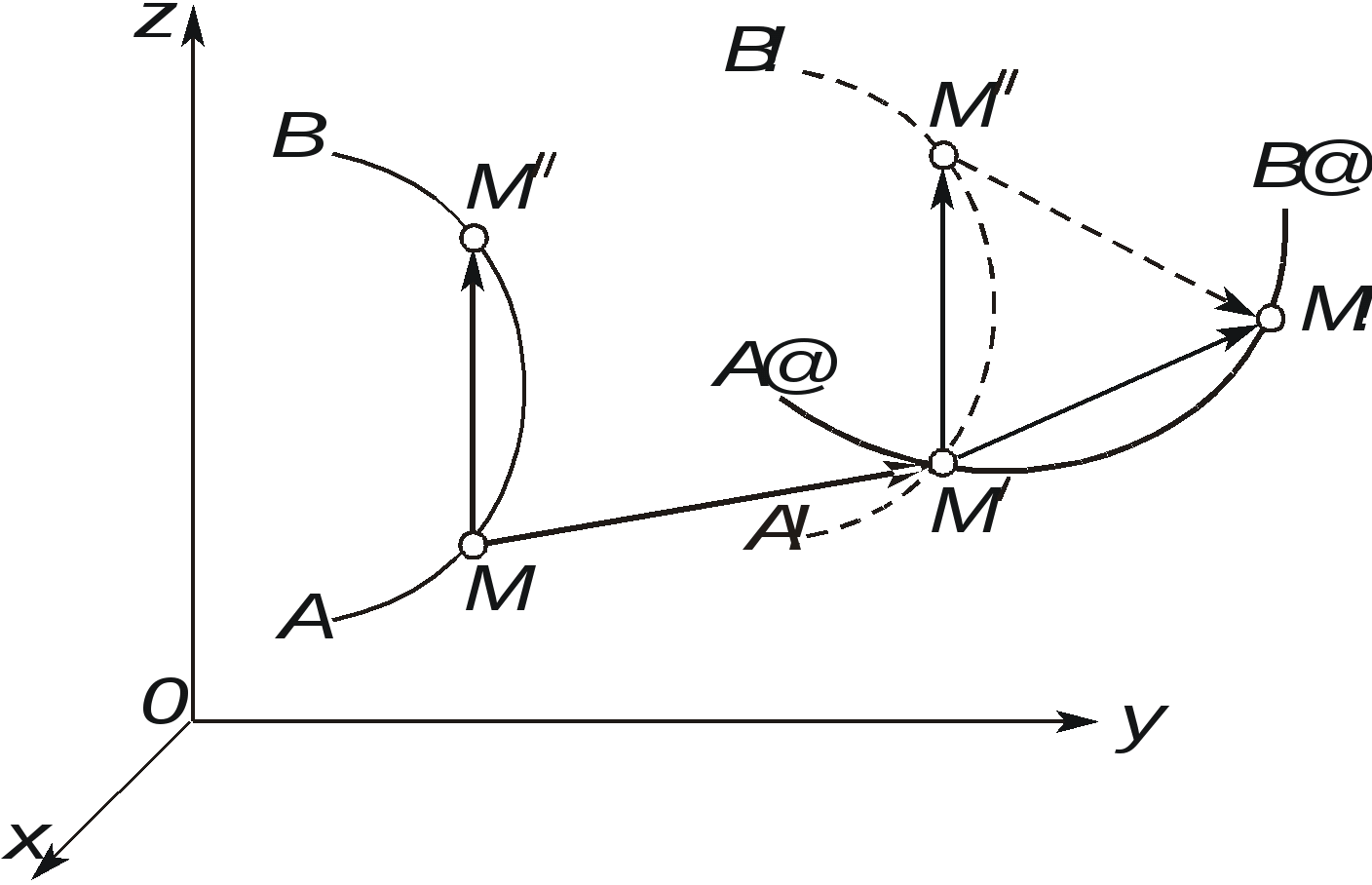 Рис. 2.32. К выводу формул сложения скоростей и ускорений Найдем абсолютное перемещение точки М за малый промежуток времени t = t1 - t . Точка М, двигаясь по кривой АВ (относительное движение), совершает за промежуток времени t относительное перемещение ММ" . В это же самое время сама кривая АВ перемещаясь с подвижными осями (переносное движение) займет положение А2В2. В результате этих двух перемещений точка М займет положение М1, относительно основной неподвижной системы отсчета 0xyz, совершив за время t абсолютное перемещение ММ1. Переносное движение относительной траектории, в свою очередь, можно считать состоящей из поступательной части (перемещение АВ в положение А1В1) и вращательной части (перемещение А1В1 в положение А2В2 вращением вокруг точки М' с мгновенной угловой скоростью Известно, что перемещение точки, разлагая его в ряд по степеням малой величины t, можно представить в виде 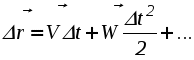 . (2.46) . (2.46) где На основании (2.46) абсолютное, относительное и переносное перемещение в (2.45) можно представить в виде : 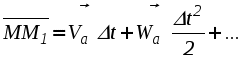 (2.47) (2.47) 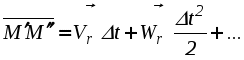 (2.48) (2.48)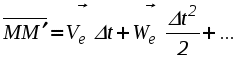 (2.49) (2.49)где Вектор Принимая во внимание равенства (2.48) и (2.50) вектор M"M1 можно представить в виде: С учетом равенств (2.47) - (2.49) и (2.51) выражение (2.45) можно переписать в виде: 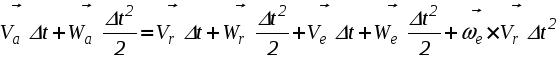 Приравнивая коэффициенты при одинаковых степенях t в левой и правой частях последнего равенства, находим: где вектор Формулу (2.52) называют формулой сложения скоростей точки в сложном движении. Согласно этой формуле, абсолютная скорость точки равна геометрической сумме ее относительной и переносной скоростей. Формулу (2.53) называют формулой сложения ускорений. Согласно (2.53), абсолютное ускорение точки в сложном движении равно геометрической сумме трех ускорений: относительного, переносного и ускорения Кориолиса. Модуль ускорения Кориолиса согласно (2.54) равен: Очевидно, что данное ускорение равно нулю: - в случае поступательного переносного движения ( e = 0 ); - когда векторы - в отдельные моменты времени, когда относительная скорость меняет свое направление на противоположное и точка (в относительном движении) должна на мгновение остановиться 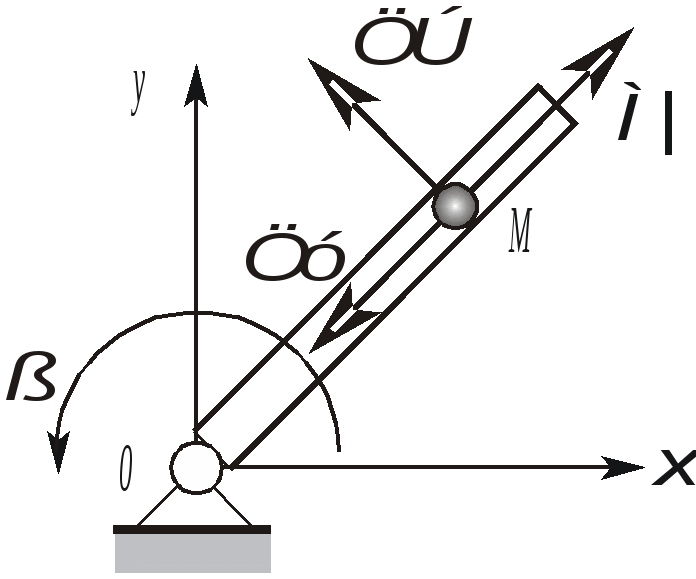 Пример 1. Точка М движется с постоянной скоростью V=1 м/с от начала координат внутри трубки, вращающейся в плоскости x0y с постоянной угловой скоростью Я = 2с-1. Определить величину абсолютного ускорения точки М в момент, когда расстояние ОМ = 0,5 м. Решение. В данной задаче движение точки М внутри трубки - относительное, вращение вместе с трубкой - переносное. Так как относительная скорость по условию задачи постоянна, то 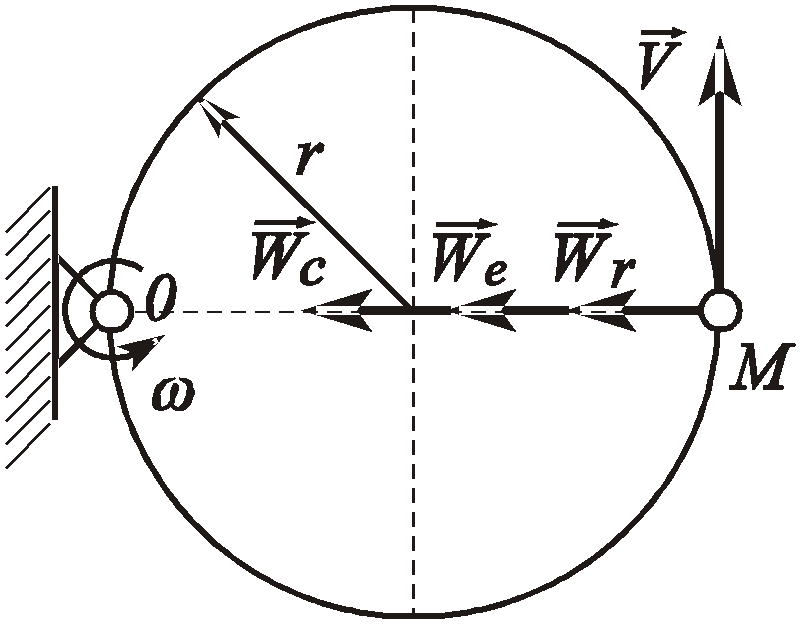 Пример 2. Кольцо радиуса r = 0,5м вращается с постоянной угловой скоростью Я = 4 рад/с в плоскости чертежа. По кольцу движется точка М с постоянной скоростью V = 2м/с. Определить величину абсолютного ускорения точки М в указанном на чертеже положении. Решение. В данной задаче движение точки М по кольцу - относительное, вращение вместе с кольцом - переносное. Для определения абсолютного ускорения воспользуемся формулой сложения ускорений: Для изучения относительного движения отвлечемся от переносного т.е. пусть кольцо не вращается, а точка М движется по кольцу с постоянной скорость V=2 м/с. Найденное в этом движении ускорение и будет относительным: = |
