лекция 3. Лекция 3 Специальность 170101 Бсіт Лектор Сушко С. А

• Название: Лекция 3 Специальность 170101 Бсіт Лектор Сушко С. А
• Дата: 30.03.2022
• Размер: 459.51 Kb.
• Имя файла: лекция 3.docx
• Тип: Лекция; #429797
• страница: 4 из 4

§4. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ СОВЕРШЕННОЙ СТОЙКОСТИ ЭНДОМОРФНОГО ШИФРА

В эндоморфных шифрах множества открытых текстов X

совпадает с множеством шифротекстов Y. По теореме 1 минимально

возможное количество K

ключей эндоморфных шифров равно

количеству Y

возможных шифротекстов, то есть

K Y.

ТеоремаШеннона(необходимые и достаточные условия совершенности эндоморфного шифра). Чтобы шифр, у которого

X Y K, был совершенно стойким, необходимо и достаточно,

чтобы: 1) для любого открытого текста x Xи шифротекста yY

существовал только один ключ k, при котором y E(x, k);

2) распределение вероятностей

P(K)

было равномерным, т.е. чтобы

вероятность выбора любого ключа k K

равнялась ¹ .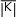

Д о к а з а т е л ь с т в о. Пусть шифр совершенно стойкий, эндоморфный. По теореме 1

^{E(x, k)} ^{ Y}

 K, где k K.

Из неравенства

k₁  k₂

следует

E(x, k₁)  E(x, k₂)

для всех x X,

а это означает, что первое условие теоремы выполнено.

Пусть множество открытых текстов X _x₁, x₂ ,..., x_N.

Произвольно выберем шифротекст yYи пронумеруем ключи так,

чтобы



E(x_i, k_i)  y, i 1, N. Тогда

p(x_i/

y) 

p(x_i)  p( y/ x_i) _

p( y)

p(x_i)  p(k_i) _.

p( y)

Так как шифр совершенно стойкий, то

Следовательно

p(x_i/

y) 

p(x_i) .

p(x_i

/ y) 

p(x_i

/ y)  p(k_i) _

p( y)

p(k_i) _{ 1}

p( y)
или

p(k_i) 

p( y)
для всех



i 1, N. Второе условие теоремы

доказано.

Пусть теперь выполнены условия 1) и 2) теоремы. На основе

условия 1) для шифротекста yYимеем:

_{1 N 1}

p( y)  _ p(x_i)  p(k_i)  _N p(x_i)  _N.

( x,k)XKi1

E_k( x) y

Откуда по условию 2) получим

p(x_i/

y) 

p(x_i)  p( y/ x_i) _

p( y)

p(x_i) .

Что и требовалось доказать Замечание. Уравнение y E(x, k)

для совершенного шифра

можно разрешить относительно ключа kпо любой известной паре (x; y)

«открытый текст – шифротекст». Отсюда у совершенного шифра длина ключа должна быть не меньше длины открытого текста.

ДОПОЛНЕНИЕ: БИБЛИОГРАФИЧЕСКИЕ СВЕДЕНИЯ

Клод Элвуд Шеннон (англ. Claude Elwood Shannon, 1916 – 2001) – американский математик и инженер, основоположник теории информации, внесший значительный вклад в теорию автоматов и теорию систем управления.

Учился по двум специальностями («Математика» и «Электротехника») в Мичиганском университете. В 1940 г. получил докторскую степень по математики. С 1941 по 1956 год изучал цепи для реализации логических функций в лаборатории Веll Labs. Во время Второй мировой войны разрабатывал криптографические системы, в частности организовал связь в для

переговорах Черчилля и Рузвельта. Его работа «Теория связи в секретных системах» стала толчком для новых достижений теории кодирования и передачи информации и придала криптографии научный статус. Разработал методы создания криптостойких систем шифрования на основе простых операций, определил условия существования совершенно стойких шифров. Статья «Математическая теория связи» (1948 г.), в которой он ввел понятие информации, сделала Шеннона всемирно известным и открыла дорогу большому числу новых работ в этой сфере.

Вышел на пенсию в 55 лет (1966 г.) и только один раз после этого (1985 г.) побывал на международном симпозиуме по теории информации в Брайтоне. Награжден национальной медалью «За научные достижения», лауреат Либмана, премии Харви.

Интересным и неожиданным было хобби Шеннона – конструирование разных устройств: от электронной мыши, способной выйти из лабиринта, до машины для жонглирования, которая так и не побила его собственный рекорд – манипулирование четырьмя шариками.