курсовая. лекция 5. Лекция 5 Расчет надежности. Описание расчета надежности

• Название: Лекция 5 Расчет надежности. Описание расчета надежности
• Анкор: курсовая
• Дата: 15.03.2022
• Размер: 3.5 Mb.
• Имя файла: лекция 5.docx
• Тип: Лекция; #398531

Лекция №5 «Расчет надежности».

1. Описание расчета надежности

Расчеты надежности - расчеты, предназначенные для определения количественных показателей надежности. Они проводятся на различных этапах разработки, создания и эксплуатации объектов.

На этапе проектирования расчет надежности производится с целью прогнозирования (предсказания) ожидаемой надежности проектируемой системы. Такое прогнозирование необходимо для обоснования предполагаемого проекта, а также для решения организационно-технических вопросов:

- выбора оптимального варианта структуры;

- способа резервирования;

- глубины и методов контроля;

- количества запасных элементов;

- периодичности профилактики.

На этапе испытаний и эксплуатации расчеты надежности проводятся для оценки количественных показателей надежности. Такие расчеты носят, как правило, характер констатации. Результаты расчетов в этом случае показывают, какой надежностью обладали объекты, прошедшие испытания или используемые в некоторых условиях эксплуатации. На основании этих расчетов разрабатываются меры по повышению надежности, определяются слабые места объекта, даются оценки его надежности и влияния на нее отдельных факторов.

Многочисленные цели расчетов привели к большому их разнообразию. На рис. 4.5.1 изображены основные виды расчетов.

Элементный расчет - определение показателей надежности объекта, обусловленных надежностью его комплектующих частей (элементов). В результате такого расчета оценивается техническое состояние объекта (вероятность того, что объект будет находиться в работоспособном состоянии, средняя наработка на отказ и т.п.).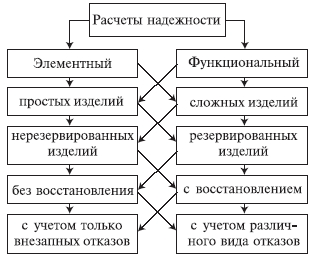



Рис. 4.5.1. Классификация расчетов надежности

Расчет функциональной надежности - определение показателей надежности выполнения заданных функций (например, вероятность того, что система очистки газа будет работать заданное время, в заданных режимах эксплуатации с сохранением всех необходимых параметров по показателям очистки). Поскольку такие показатели зависят от ряда действующих факторов, то, как правило, расчет функциональной надежности более сложен, чем элементный расчет.

Выбирая на рис 4.5.1 варианты перемещений по пути, указанному стрелками, каждый раз получаем новый вид (случай) расчета.

Самый простой расчет - расчет, характеристики которого представлены на рис. 4.5.1 слева: элементный расчет аппаратурной надежности простых изделий, нерезервированных, без учета восстановлений работоспособности при условии, что время работы до отказа подчинено экспоненциальному распределению.

Самый сложный расчет - расчет, характеристики которого представлены на рис. 4.5.1 справа: функциональной надежности сложных резервированных систем с учетом восстановления их работоспособности и различных законов распределения времени работы и времени восстановления.

Выбор того или иного вида расчета надежности определяется заданием на расчет надежности. На основании задания и последующего изучения работы устройства (по его техническому описанию) составляется алгоритм расчета надежности, т.е. последовательность этапов расчета и расчетные формулы.

2. Расчеты надежности технической системы

Расчеты показателей надежности технического устройства, как системы, состоящей из совокупности материальных элементов, проводятся исходя из постулата, что вся система и любой ее элемент могут находиться только в одном из двух возможных состояний – работоспособном и неработоспособном, при этом отказы элементов являются независимыми друг от друга. Работоспособность состояния системы определяется работоспособностью состоянием элементов и их взаимными связями. Расчет надежности любой технической системы в простейшем варианте реализовать как полный перебор всех возможных комбинаций состояний элементов с определением вероятности каждого из них и установлением работоспособных состояний системы.

Такой метод является универсальным и может использоваться при расчете практически любых ТС. Однако при большом количестве элементов системы такой метод является нецелесообразным, а часто и просто нереальным, вследствие огромного объема вычислений, поэтому в практических расчетах применяют более эффективные и экономичные методы расчета, не связанные с существенными объемами вычислений. Эти методы основаны на исследовании структуры ТС и построении эквивалентных структурных схем.

Методика расчета надежности устройств программно-аппаратного комплекса вычислительной системы состоит из следующего набора операций:

• 
  определение типа элемента и его характеристик, формулирование четкого формального понятия отказа для всей системы и его отдельных составных частей;
  
• 
  анализ структуры устройства, определение основных и вспомогательных блоков системы, составление эквивалентной схема расчета надежности, в которой элементами расчета являются конструктивно оформленные блоки;
  
• 
  выбор метода расчета с подбором справочных данных и форм представления информации, определение параметров нагрузки элементов и влияния внешней среды;
  
• 
  определение интенсивности отказов и вероятности безотказной работы каждого элемента;
  
• 
  определения интенсивности отказов и вероятности безотказной работы системы, расчет других показателей надежности, представление результатов расчета.
  

Построение эквивалентной структурной схемы при расчете надежности используется слияние нескольких элементов, соединенных определенным образов, в один – эквивалентный, безотказность работы которого в точности будет равна заменяемой совокупности элементов. При этом рассматриваются типовые схемы соединения элементов – последовательное, параллельное и мостиковое.

В системе из последовательно соединенных элементов отказ любого

элемента приводит к отказу всей системы (рис. 5, а). Так как отказы элементов являются независимыми, то вероятность одновременной безотказной работы последовательно соединенных n элементов определяется в соответствии с теоремой умножения вероятностей так - вероятность совместного появления независимых событий равна произведению вероятностей этих событий:



Соответственно, вероятность отказа такой системы составит:



Набор из параллельным соединением элементов представляет собой систему, отказ которой произойдет только в случае, когда откажут всех ее

элементы (рис.5, б). Такие структуры характерны для устройств, в которых

элементы дублируются или резервируются, потому что параллельное соединение применяется как основной метод повышения надежности.

Рис. 5. Системы с последовательным (а), параллельным (б) и мостиковым (в) соединением элементов

При допущении независимости отказов вероятность отказа такой системы может быть найдена так же по теореме умножения вероятностей, но как произведение вероятностей отказа элементов:



Тогда вероятность безотказной работы параллельно соединенных элементов составит:



Мостиковая структура (рис. 5, в) не приводится ни к параллельному ни к последовательному соединениям. Она представляет собой параллельно соединенные последовательные цепочки элементов с диагональными элементами, которые включены между узлами параллельных ветвей (рис. 5, в).

Работоспособность мостиковой определяется не только количеством отказавших элементов, но и их положением в структурной схеме. Для расчета надежности мостиковых систем можно воспользоваться методом прямого перебора или метод логических схем с применением алгебры логики. Последний сводится к составлению логического выражения, которое является условием работоспособности системы. Для каждого элемента и системы также используются два противоположных логических состояния - отказ или состояние работоспособности.

Реальные технические системы в большинстве своем имеют сложную комбинированную структуру, где отдельные группы элементов могут образовывать последовательные, параллельное, или мостиковые схемы соединений.

В этих случаях следует предварительно произвести декомпозицию исходной схемы надежности, разбив ее на простые группы элементов, методика расчета надежности которых известна, после чего заменить эти группы в новой структурной схеме эквивалентными квазиэлементами, вероятности безотказной работы которых будут равны вычисленным вероятностям безотказной работы этих групп. Данную процедуру при необходимости можно выполнять несколько раз, до тех пор, пока получившаяся схема надежности не превратится в структуру, методика расчета надежности является известной и наиболее простой [11].

3. Расчет показателей надежности элементов системы по статистическим данным

Система состоит из М восстанавливаемых элементов. В процессе эксплуатации в течение K лет возникали отказы элементов. Во время простоя отказавший элемент восстанавливался и вновь вводился в эксплуатацию. Определить оценки показателей надежности: безотказности и ремонтопригодности – для случая полной и частичной статистики отказов.

Указания. Если за K лет собрана представительная (полная) статистика о числе случаев nj простоя каждого j-го элемента системы и известны данные о длительностях пребывания τi их в таком состоянии, то можно определить среднее время простоя τoi по формуле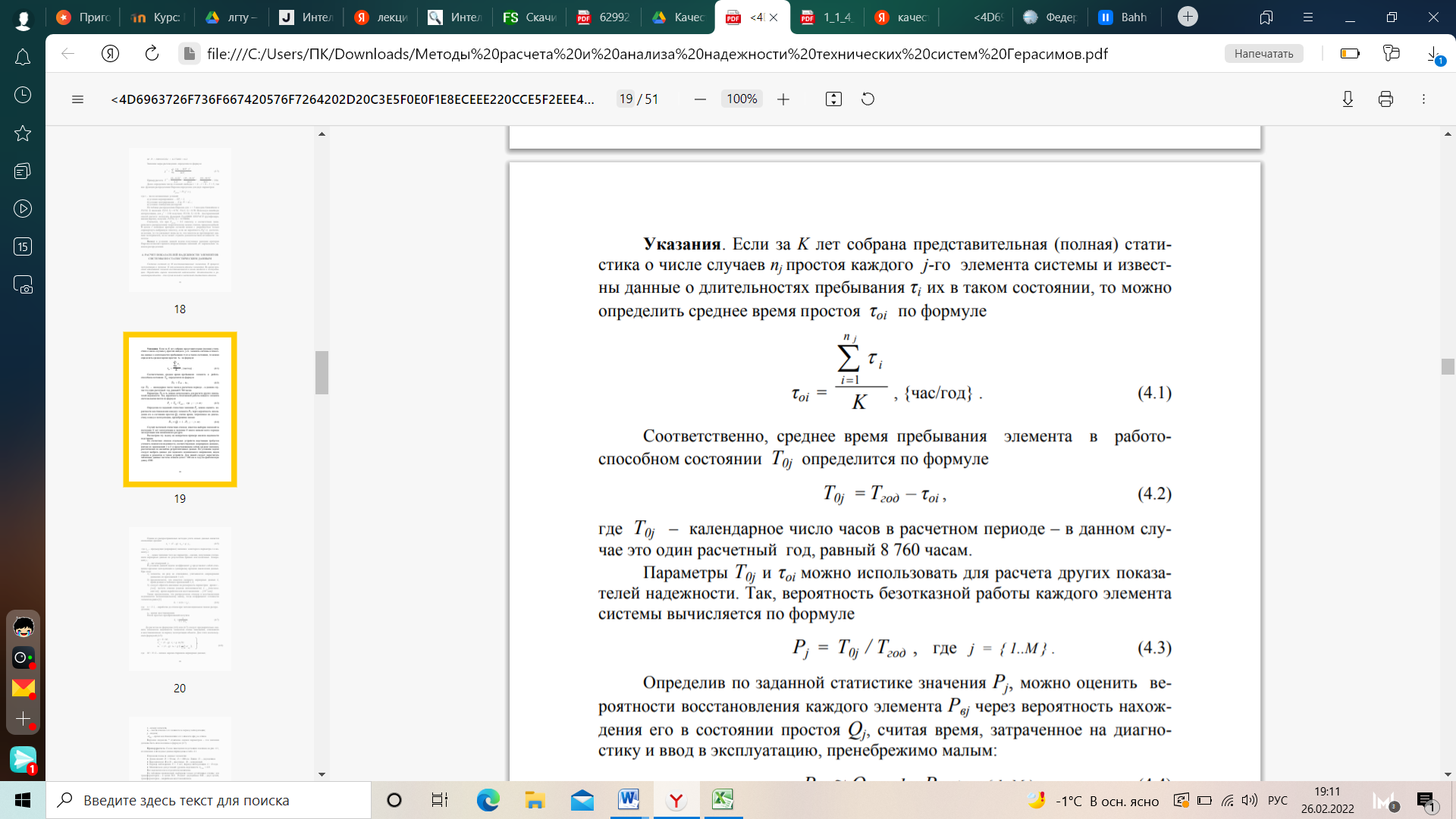



Соответственно, среднее время пребывания элемента в работоспособном состоянии T0j определится по формуле:



где T0j – календарное число часов в расчетном периоде – в данном случае это один расчетный год, равный 8 760 часам.

Параметры T0j и τoi можно использовать для расчета других показателей надежности. Так, вероятность безотказной работы каждого элемента системы вычисляется по формуле:



Определив по заданной статистике значения Pj, можно оценить вероятности восстановления каждого элемента Pвj через вероятность нахождения его в состоянии простоя Qj, считая время, затраченное на диагностику и ввод в эксплуатацию, пренебрежимо малым:



Случай частичной статистики отказов: известна выборка значений за последние N лет эксплуатации и значение N много меньше всего периода эксплуатации или назначенного ресурса.

Рассмотрим эту задачу на конкретном примере анализа надежности

подстанции.

По статистике отказов отдельных устройств подстанции требуется уточнить показатели надежности, соответствующие «априорным данным», взятым из приложений 1 и 2 и представляющим собой средние значения, рассчитанные по ансамблю ретроспективных данных. По условиям задачи следует выбрать данные для заданного номинального напряжения, видов отказов и ремонтов и типов устройств. Для линий следует пересчитать табличные данные частоты отказов (откл./ 100 км в год) на фактическую длину ЛЭП.

Одним из распространенных методов учета новых данных является скользящее среднее:



где хt-1 – предыдущее (априорное) значение некоторого параметра х к моменту t;

хt – новое значение того же параметра – оценка, полученная уточнением априорных данных по результатам прямых или косвенных измерений yt;

g – вес измерений yt .

В условиях данной задачи коэффициент g представляет собой отношение времени эксплуатации к суммарному времени накопления данных.

При этом:

1. 
   элементы, ни разу не отказавшие, учитываются «априорными данными» из приложений 1 и 2;
   
2. 
   предполагается, что известен «возраст» априорных данных L, приведенных в таблицах приложений 1, 2;
   
3. 
   следует обратить внимание на размерность параметров: время t – [год], частота отказов (оценка интенсивности)  – [отключений/год], время наработки или восстановления – [10–3 лет];
   

Также предположим, что распределение отказов и восстановления подчиняются экспоненциальному закону, тогда коэффициент готовности

элементов равен [1]



где t0 = 1/λ, – наработка до отказа при экспоненциальном законе распределения; tв – время восстановления.

После простых преобразований получим: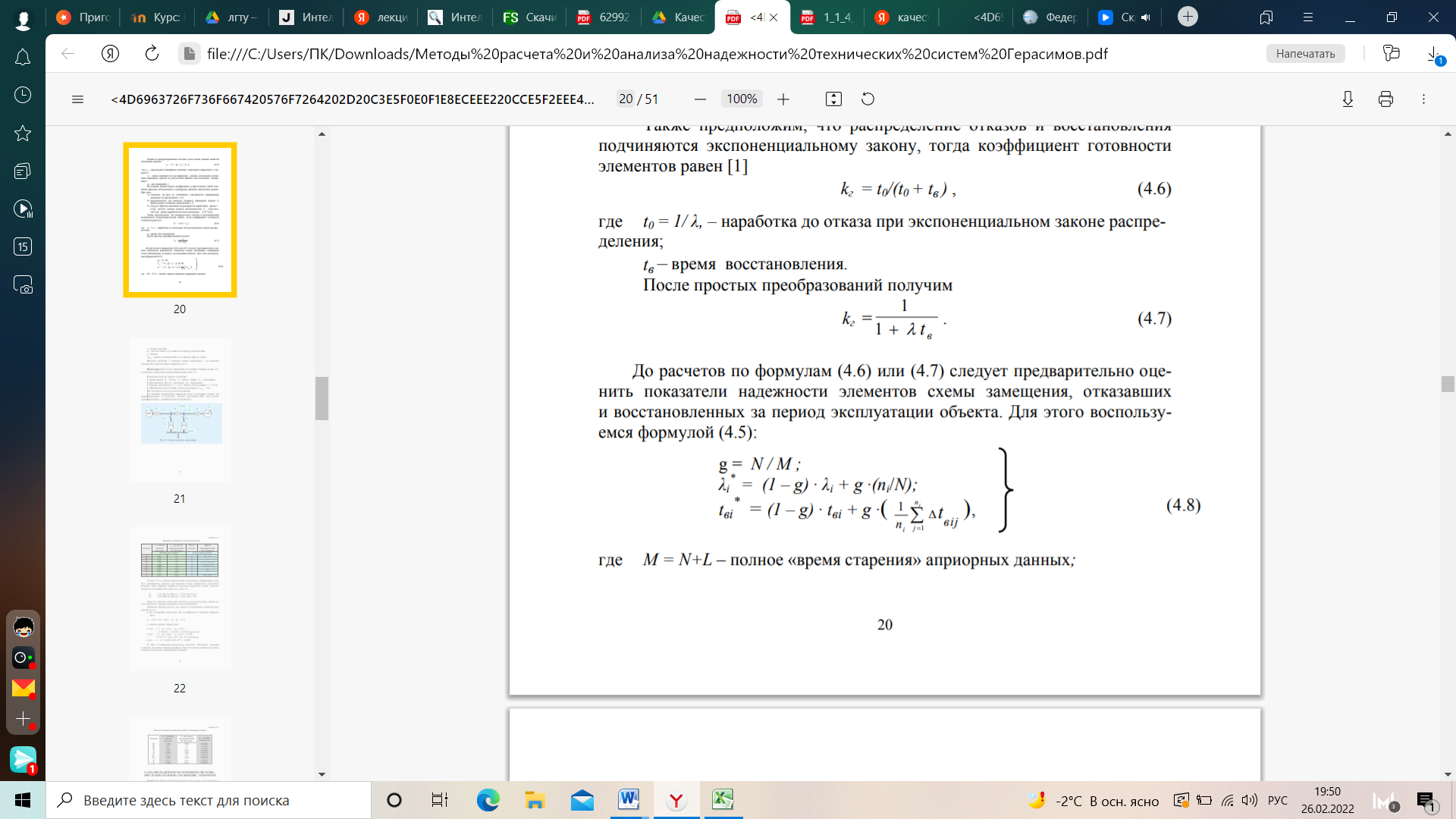



До расчетов по формулам (4.6) или (4.7) следует предварительно оценить показатели надежности элементов схемы замещения, отказавших и восстановленных за период эксплуатации объекта. Для этого воспользуемся формулой (4.5):



где M = N+L – полное «время старения» априорных данных;