Электротехника теория. Однофазные электрические цепи

• Название: Однофазные электрические цепи
• Анкор: Электротехника теория
• Дата: 17.09.2022
• Размер: 1.6 Mb.
• Имя файла: Elektrotekhnika_bilety.docx
• Тип: Документы; #681944
• страница: 1 из 10

Однофазные электрические цепи.

1. 
   Основные понятия и определения.
   

Эл. цепью называют совокупность эл. технических устройств, соединенных определенным образом и обеспечивающих путь току.

Эл. Схема – графическое изображение электрической цепи, с использованием условных обозначений элементов и показывающее соединение их друг с другом. Элементами цепи являются:

Ветвь- участок, через который замыкается один и тот же ток

Узел- место соединения трех и более ветвей(обозначается точкой)

Контур – замкнутый путь , включающий несколько ветвей.

Ток – упорядоченное движение частиц или квазичастиц- носителей заряда. Проявление: нагревание проводников, изменение хим состава проводников, создание магнитного поля.

Напряжение – физ величина, значение которой равно работе эффективного эл поля, совершаемого при переносе единичного пробного эл заряда из точки А в точку Б

ЭДС- скалярная величина, характеризующая работу сторонних сил, действующих в квазистационарных цепях постоянного или переменного тока

Переменный ток – ток, изменяющийся во времени по значению и направлению.

Периодический переменный ток – ток, кривая изменения которого повторяется через равные промежутки времени(периоды)

Период-отрезок времени, который показывает одно полное изменение. В большой энергетике применяют синусоидальные переменные периодичные токи. Частота – число периодов в секунду f=1/T (Гц) , промышленная частота = 50 Гц

Для аналитической записи синусоиды i=I_msinα, аргументом является угол α=ωt , ω-коэффициент пропорциональности.

Фаза-аргумент синуса. В трехфазной цепи, фаза - участок цепи. В однофазной - аргумент синуса

α =ωt α=2π => ω=2π/T = 2πf –угловая частота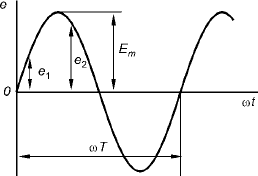

I_m E_m U_m - максимальные амплитудные зн-я

i,e,u – мгновенные значения
Максимальные значения являются частными случаями мгновенных.

2. 
   Действующие и средние значения синусоидальных величин (ЭДС, напряжения и тока).
   

Действующие значения переменного тока – значение постоянного тока, при котором в резисторе R за период Т выделяется столько же тепловой энергии, что и при переменном синусоидальном токе.

Для синусоидального тока действующее значение

I=I_m/√2=0.707I_m E=E_m/√2=0.707 E_m U=U_m/√2=0.707 U_m

Средним значением переменного тока называют такое значение постоянного тока при котором за Т/2 переносится такой же электрический заряд, что и при переменном токе.

Среднее значение – среднее арифметическое

I_ср=2I_m/π= 0.637 I_m E_ср=2E_m/π= 0.637 E_m U_ср=2U_m/π= 0.637 U_m

Коэффициент формы кривой – называют отношение действующего значения к среднему. Характеризует пиковость кривой. Чем больше отличается от 1, тем более пиковый характер носит криая.

Для синусоидальной кривой коэффициент форы k_ф=I/I_cp = 1.11

3. 
   Изображение синусоидальных величин в прямоугольных координатах.
   

В общем случае синусоидальные величины записывают

i=I_msin(ωt±ψ_i) e=E_msin(ωt±ψ_e) u=U_msin(ωt±ψ_u)

ψ- начальная фаза – значение фазового угла при t=0 Фаза – угол, являющийся аргументом синуса

Две синусоидальные величины совпадают по фазе, если они одновременно проходят через нулевые и максимальные значения

Две синусоидальные величины находятся в противофазе, если они одновременно проходят через нулевые значения

Если две синусоидальные величины имеют разные начальные фазы, то говорят, что они сдвинуты по фазе i1=Imsin(ωt+ψi1) i2=Imsin(ωt+ψi2).

Положительные начальные фазы откладывают влево от начала координат, отрицательные – вправо. Если ψ2> ψ1, то говорят, что i2 опережает по фазе i1, или

i1 отстает
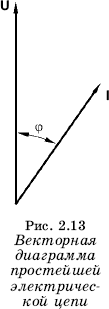
Большое хозяйственное значение имеет сдвиг по фазе между напряжением и током

i=I_msin(ωt+ψ_i) u=U_msin(ωt+ψ) φ= ψ_u- ψ_i

Сдвиг по фазе между напряжением и током обозначают φ, φ-положительный, если

ψ_u> ψ_i

4. Векторное изображение синусоидальных величин.

При графическом сложении и вычитании синусоид, точность операции зависит от измерительного инструмента, масштаба, от количества выбранных ординат. Большой точности достичь невозможно. Векторное изображение упрощает операции сложения и увеличивает точность.
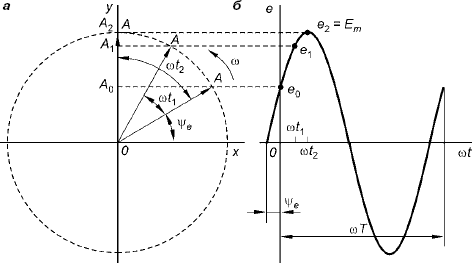
Рассмотрим e=Emsin(ωt+ψe)

На рис 1 отложим вектор ОА, длина которого равна амплитуде Е. |ОА|=Еm под углом ψe к оси ОХ. На оси ординат рис 2 отложим проекции этого вектора на ось ОУ. При t1=0, проекция вектора ОА на ОУ равна OA0= ОАsinψe= Emsinψe = e0

Будем вращать вектор ОА с частотой ω в направлении против часовой стрелки. Через некоторое время он повернется на угол ωt1, и будет составлять с осью ОХ угол равный ωt1+ ψe ,проекция вектора ОА на ОУ = ОАsin(ωt1+ ψe)= Emsin(ωt1+ψe)=e1

При t=t2 вектор ОА направлен по оси ОУ и его проекция ОА=Em= e2 Из построений видно, что проекции вращающегося вектора на ось ОУ изменяются по синусоидальному закону, то есть представляют собой

мгновенные значения синусоидальной ЭДС. Справедливо и обратное: любую

синусоидальную величину можно изображать вращающимся вектором, длина которого равна амплитуде

Векторами можно изображать и действующие значения, но вращать их нельзя, т.к. их проекция ничего не изображают. Если векторы всех синусоидальных величин вращать с одной частотой, то их взаимное положение на плоскости неизменно и векторы можно не вращать. Изображенные синусоидальные величины векторами можно геометрически складывать и вычитать.

Векторная диаграмма – совокупность векторов синусоидальных величин, изображающих электромагнитные процессы в цепи, построенных с учетом их правильного взаимного расположения на плоскости.

Выводы: 1. Векторами можно изображать только амплитудные величины.2. На ВД можно изображать только синусоид величины, измен с одинаковой частотой.





5.Комплексный метод расчета

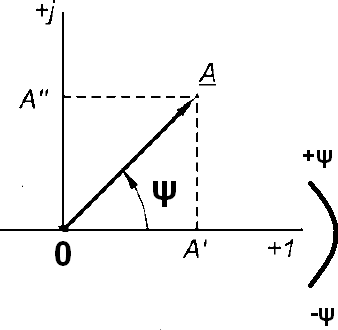
Основан на теории комплексных чисел А- комплексное число(КЧ)

А΄- вещественная составляющая

А΄΄- мнимая составляющая

Алгебраическая форма записи комплексного числа :

А= А΄+j А΄΄

А΄=Acosψ А΄΄=Asinψ , где А-длина вектора

А=А(cosψ+jsinψ)- тригонометрическая форма записи комплексных чисел.

По формуле Эйлера : cosψ+jsinψ=ejψ е-основание ln Показательная форма записи: А=А ejψ А-модуль КЧ

e jψ-поворотный множитель, показывает на какой угол по отношению к оси +1 надо повернуть вектор. Положительные углы откладывают против ч.с., отрицательные- по ч.с. ψ – аргумент КЧ

e±jπ/2 =±j j- мнимая единица.

Любой точке на комплексной плоскости соответствует только 1 вектор, проведенный в эту точку из начала координат => справедливо обратное . Любой вектор можно описать КЧ соответствующим его концу. Описывая векторы КЧ-ми можно пользоваться алгеброй КЧ-а.

При сложении и вычитании удобнее пользоваться алгебраической формой записи( вещ 1±вещ 2, мним 1±мним2)

Умножение, делении, возведение в степень, извлечение корня удобнее производить пользуясь показательной формой записи.

А1=А1 ejψ1 А2=А2 ejψ2 А1/А2 =А1/А2 ej(ψ1- ψ2)

Если КЧ задано в алгебраической форме записи, то для перевода в показ форму записи надо воспользоваться формулой : А=√(A΄2+A΄΄2) ψ=arctg(A΄΄/A΄)

Если КЧ задано в показательной форме записи то для перехода в алгебраич форму надо воспользоваться формулами : А΄=Acosψ А΄΄=Asinψ

Аргументом КЧ какого либо вектора явл угол между вектором и осью +1.

В электротехнике при изображении вектора синусоидальных величин этот угол был равен начальной фазе. Поэтому синусоидальное напряжение u=Umsin(ωt+ψu) изоб- ся КЧ:

Um=Umejψu -комплексное амплитудное напряжение

U=Uejψu - действующее напряжение.




6.Законы Кирхгофа

1. 
   з-н Кирхгофа относится к узлу цепи, гласит следующее: Сумма токов в узле =0 Для мгновенных значение – сумма алгебраическая, для максимальных и действительных – только векторная, или в комплексном виде
   

Для мгновенных значений: Для действительных значений:

n

∑ i_k = 0

k=1

n

∑ I_k = 0

k=1

При написании уравнений токи направленные к узлу «+», от узла «-» Направление тока в ветвях может быть только условным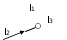
I₁+I₂- I₃=0 I₁+ I₂= I₃

Вторая формулировка: Σтоков направленных к узлу = Σтоков, направленных от узла

2. 
   з-н Кирхгофа относится к замкнутому контуру: ΣЭДС в замкнутом контуре =Σ падений напряжений в нем
   

Для мгновенных значений – сумма алгебраическая

Для действующих и максимальных – векторная или комплексная

Для мгновенных значений: Для действительных значений:

n n

n n

∑ e_k = ∑ u_k ∑E_k = ∑U_k

k=1

k=1
k=1

k=1

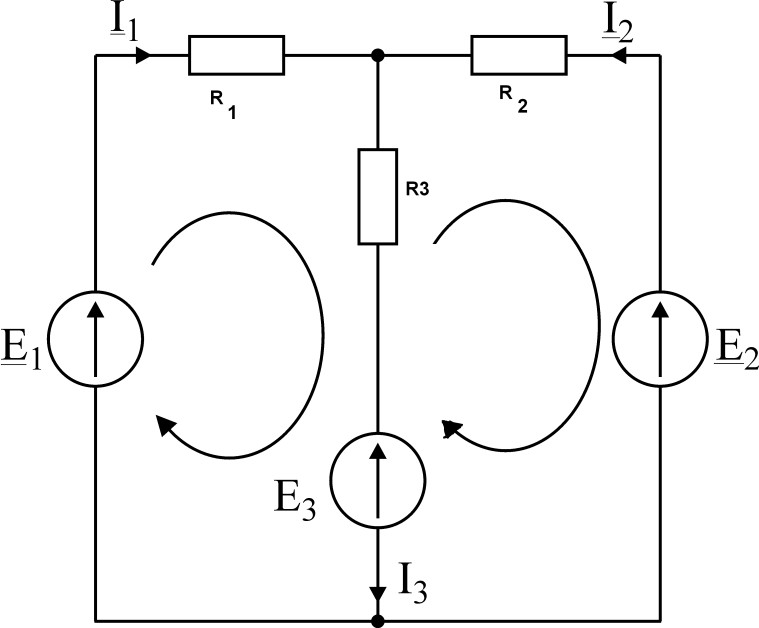При написании уравнений произвольно задают условно положительные направления ЭДС и тока в ветвях. Задают направление обхода контура. Если направление ЭДС совпадает с направление обхода «+». Если направление тока в ветви совпадает с направлением обхода, то напряжение на этой ветви «+»