Электротехника теория. Однофазные электрические цепи

• Название: Однофазные электрические цепи
• Анкор: Электротехника теория
• Дата: 17.09.2022
• Размер: 1.6 Mb.
• Имя файла: Elektrotekhnika_bilety.docx
• Тип: Документы; #681944
• страница: 2 из 10

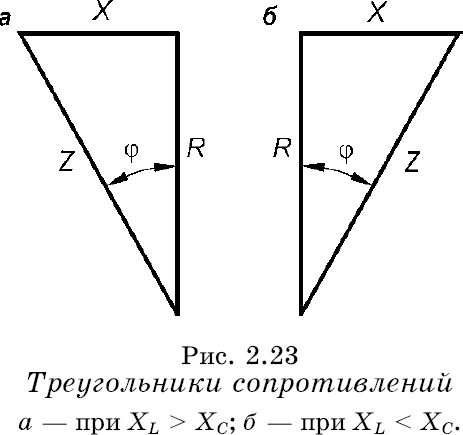
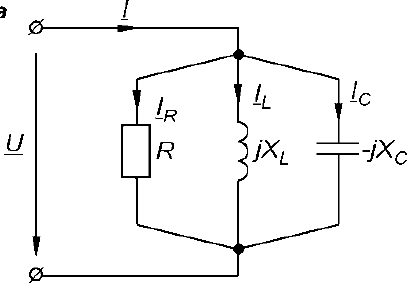
1) E₁=R₁I₁+ R₃I₃

2) – E₂= - R₂I₂- R₃I₃

7,8,9.Электрическая цепь с R,L и С

С резистором: Ток – движение заряженных частиц.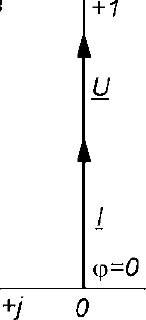



Элементы, обладающие только активным сопротивлением R называют резисторами Задано: u=U_msinωt , R Найти: i, I_m,ψ_i

По 2 з-ну Кирхгофа имеем: Ri-u=0 i=u/R=U_msinωt/R= I_msinωt ψ_i=0

I_m=U_m/R если:√2 I =U/R U= U I=I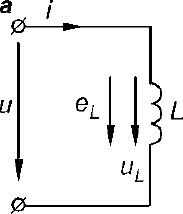

С индуктивностью: Индуктивностью обладают все проводники, но значительную индуктивностью имеют катушки, обмотки, состоящие из большого числа витков. Задано: u=U_msinωt Найти: i, I_m,ψ_i. Рассмотрим идеальную индуктивность (R=0) Ток в цепи с индуктивностью создает магнитный поток Ф, поток Ф индуцирует ЭДС: i→Ф→e_L Положит ЭДС совпадает с направлением тока . По 2 з- ну Кирхгофа имеем:

e_L= -u По закону электромагнитной индукции e_L= -L*di/dt

-L*di/dt = - u di/dt=u/L=U_msinωt/L → i= I_msin(ωt-π/2) I_m=U_m/ ωL I=U/ ωL [ωL]=Ом X_L= ωL=2πfL-индуктивное сопротивление частоте и индуктивности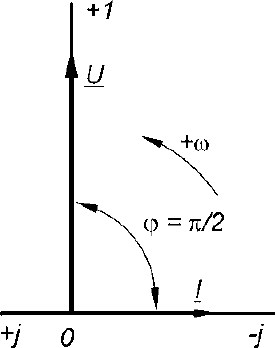

I=U/ X_L U = X_L* I ψ_i=-π/2

В цепи с индуктивностью ток отстает по фазе от напряжения на π/2 Если вектор тока I умножить на X_L , получим ветор X_LI

Если X *j= e^π/2, чему соответствует поворот на + π/2 , в результате вектор, модуль которого равен напряжению совпадает по фазе с напряжением

U=U I=Ie-^jπ/2=-jI ψ=ψ_u- ψ_i=0-(-π/2)=π/2

Напряжние в цепи с индуктивностью : U_L=jX_LI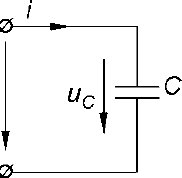

С электроемкостью : Задано: u=U_msinωt Найти: i, I_m,ψ_i (R=0) Значительной емкостью обладают конденсаторы, состоящие из двух пластин изолированных друг от друга диэлектриком. Емкость С называют тот электрический заряд, который скапливается на пластинках, при напряжении на них 1 Вольт. Поэтому электрический заряд Q=Cu_c u_c – напряжение на конденсаторе. По второму закону Кирхгофа имеем: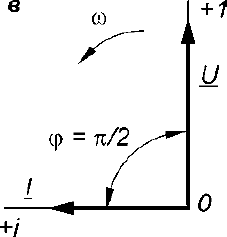

u_c=u тогда Q=Cu_c=CU_msinωt i=I_msin(ωt+π/2) I_m=Um/(1/ωC) [1/ωC]= Ом X_C=1/ωC=1/2πfC X_c- емкостное сопротивление

X_c 1/ f,C

I=U/ X_c з-н Ома u_c=X_cI

В цепи с емкостью ток опережает напряжение по фазе на π/2 U_c = -jX_c* I

I=Ie^jπ/2=jI

10.Эл цепь при последовательном соединении с R,L и С Последовательное соединение – соединение, при котором во всех элементах существует один ток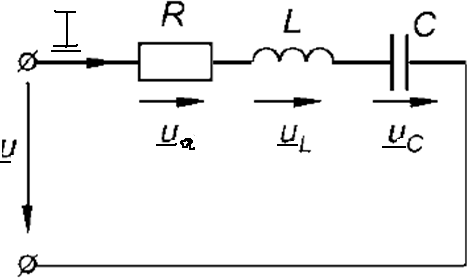

Во 2 з-ну Кирхгофа : U=U_R+U_L+U_C

U-U_R-U_L-U_C=0 U=RI+jX_LI-jX_cU= R+j(X_L-X_C)I R+j(X_L- X_C)=R+jX=Z

U=ZI→I=U/Z – з-н Ома для цепи пер тока R-активное X-реактивное Z- полное

Z=U/I, если U=Ue^jψu I=Ie^jψi Z=Ue^jψ/I=Ze^jψ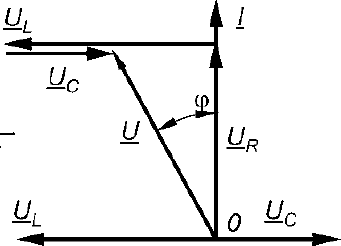

Полное комплексное зависит от φ(аргумент комплексного сопротивления) φ=arctgX/R=arctg(X_L-X_C)/R=(ωL-1/ωC)/R φ зависит от параметров цепи R,L,C и частоты f. Построим векторную диаграмму

напряжений. За начальный вектор принимаем вектор тока, т.к. он одинаков во всех элементах

Вектор напряжений на элементе с R U_R совпадает по фазе с током Вектор U_L опережает ток на 90 Вектор U_С отстает от тока на 90

U=U_R+U_L+U_C

U-полное Ua-активная Up-реактивная Прямоугольный треугольник ОАВ катетами

которого явл активная и реактивная напряжн, а гипотенузой –полное напряжение называется треугольником напряжений. Соотношения

U_a=Ucosφ U_p=Usinφ U_p= U_L+U_C U=√ (U_a²+ U_p²) = √ (U_a²+(U_L- U_C) ²) φ= arctg U_p/ U_a

Вид треугольника напржений зависит от соотношениями между X_L и X_c

После деления всех сторон треугольника напряжений на ток I получим треугольник сопротивлений, стороны которого равны

U_a/I=R U_p/I=X U/I=Z

соотношения: R=Zcosφ X=Zsinφ Z=√(R²+X²)

φ=arctgX/R

Реактивное: Х=X_L-X_C если X_L>X_C то Х>0

если X_LC то Х<0

φ=arctg(X_L-X_C)/R имеет знак зависящий от X_L и X_C

11.Эл цепь при параллельном соединении с R,L и С Параллельным соединением называют такое соединение, при котором ко всем элементам подводят одно и то же соединение. Токи в параллельных ветвях определяют по закону Ома