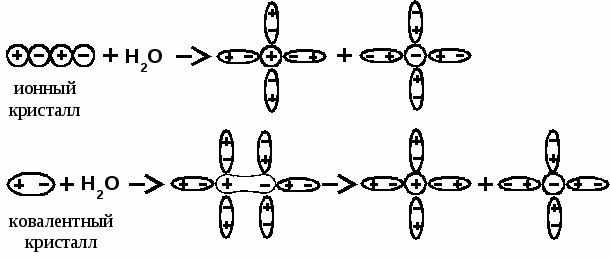ЛЕКЦИЯ 07. Лекция 7 Свойства растворов электролитов. Теория электролитической диссоциации Аррениуса. Закон разведения Оствальда. Понятие об электролитической теории ДебаяГюккеля.

• Название: Лекция 7 Свойства растворов электролитов. Теория электролитической диссоциации Аррениуса. Закон разведения Оствальда. Понятие об электролитической теории ДебаяГюккеля.
• Анкор: ЛЕКЦИЯ 07.doc
• Дата: 15.02.2018
• Размер: 235 Kb.
• Имя файла: ЛЕКЦИЯ 07.doc
• Тип: Лекция; #15569

ЛЕКЦИЯ 7

Свойства растворов электролитов. Теория электролитической диссоциации Аррениуса. Закон разведения Оствальда. Понятие об электролитической теории Дебая-Гюккеля. Активность и коэффициент активности электролитов. Средняя ионная активность и средний ионный коэффициент активности. Правило ионной силы.

Электрохимия – раздел физической химии, изучающий связь между химическими процессами и электрическими явлениями.

7.1 Свойства растворов электролитов. Закон разведения Оствальда. Теория электролитической диссоциации Аррениуса.

По способности проводить электрический ток растворы можно подразделить на два класса – электролиты и неэлектролиты

Электролиты – это вещества, которые в растворе и в расплаве диссоциируют на ионы и проводят электрический ток. Сюда же относятся и твердые электролиты.

В 1883 году С. Аррениус сформулировал основные положения теории о физической природе электролитов, которые получили название теории электролитической диссоциации Аррениуса.

1. 
   Молекулы электролита подвергаются в растворах диссоциации на катионы и анионы.
   
2. 
   Диссоциация может быть полной или частичной. она характеризуется степенью диссоциации α.
   
3. 
   По способности к диссоциации электролиты были разделены на слабые и сильные.
   

• 
  сильные электролиты - вещества, полностью диссоциирующие в растворе (α ≈ 1).
  
• 
  слабые электролиты - вещества, диссоциирующие в растворе лишь частично ( α < 1).
  

4. 
   Согласно теории диссоциации Аррениуса взаимодействие между ионами отсутствует (как в идеальном газе). На самом деле молекулы, образовавшиеся при диссоциации, и ионы находятся в равновесии между собой. Процесс диссоциации обратим. Причина диссоциации   это в
   заимодействие растворенного вещества с молекулами растворителя (рис. 1).
   

Рис. 1.

Э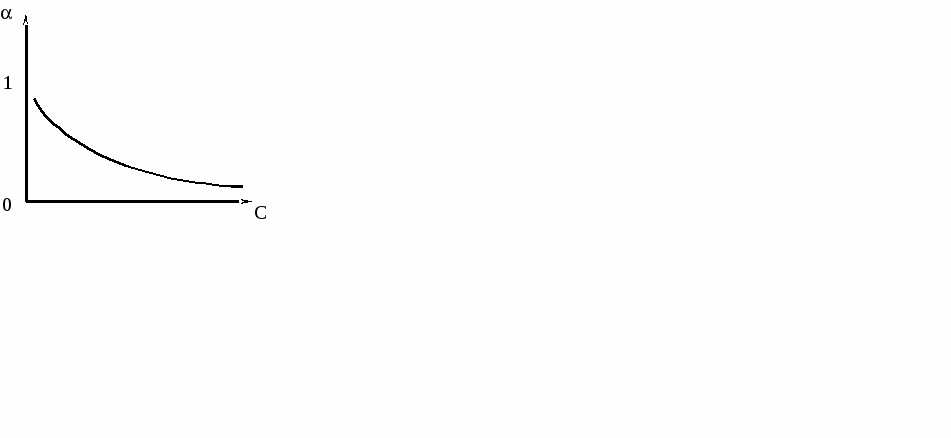
лектропроводность слабых электролитов определяется степенью диссоциации (), величина которой зависит от концентрации электролита и температуры (рис. 2).

Рис. 2.

Степень диссоциации – это отношение числа частиц (молекул), растворившихся на ионы к числу растворенных частиц (молекул).

α ≤ 1

По величине степени диссоциации судить о силе электролита не очень удобно, так как величина зависит от многих параметров, особенно от концентрации. Более удобно использовать величину константы диссоциации К_д (К_{равновесия}).

Рассмотрим равновесие диссоциации слабого бинарного электролита, например,

.

Пусть С₀ - начальная концентрация СН₃СООН, тогда

,

, .

Запишем константу диссоциации

. (1)

Выражение (1) называют законом разведения Оствальда для бинарных электролитов. Для более сложных электролитов выражение для К_Д, будет иметь иной вид.

Как любая константа равновесия, константа диссоциации зависит от температуры, поэтому сила электролита меняется с изменением температуры.

Для описания коллигативных свойств растворов электролитов используют изотонический коэффициент.

Изотонический коэффициент ( i ) - это отношение числа всех частиц в растворе к числу растворенных частиц.

i ≥ 1. (2)

Изотонический коэффициент показывает, во сколько раз суммарная эффективная концентрация недиссоциированных молекул и ионов в растворе больше начальной концентрации молекул до диссоциации. С ростом концентрации коэффициент уменьшается.

Рассмотрим как связаны и . Пусть ν – число ионов, на которые распадается частица (молекула) тогда , (3)

Если α = 0 (неэлектролит), то i = 1,

если α = 1 (сильный электролит), то, например, для NaCl i = 2.

Экспериментально величину i можно найти путем сравнения опытных значений осмотических давлений растворов, значений понижения температуры замерзания или повышения температуры кипения растворов со значениями, вычисленными в предположении, что i = 1 (расчетные величины):

. (4)

Следует помнить, что i ≥ 1 для растворов электролитов (они диссоциируют), если же молекулы в растворе ассоциируют (например, из двух молекул образуется одна частица за счёт водородных связей), то i < 1.
7.2 Активность и коэффициент активности электролитов. Средняя ионная активность и средний ионный коэффициент активности

В связи с электростатическим взаимодействием в растворе даже для разбавленных растворов сильных электролитов концентрации в уравнениях термодинамики должны быть заменены активностями. Например, если для иона как и для компонента в растворе справедливо выражение

, (5)

где с_i – концентрация i-го иона в идеальном растворе, то для реального раствора будем иметь:

, (6)

где a_i = c_i·f_i — активность i-го иона в растворе,

f_i – коэффициент активности.

Тогда энергия взаимодействия иона с окружающими его ионами в расчете на 1 моль ионов равна

, (7)

f_i→1 при с→0

Таким образом, величина коэффициента активности, главным образом зависящая от силы электростатического взаимодействия ионов, а также ряда других эффектов, характеризует степень отклонения свойств реальных растворов электролитов от идеальных растворов. По смыслу f_i это работа по переносу иона из идеального раствора в реальный.

Различают активность электролита и активность ионов. Для любого электролита процесс диссоциации можно записать следующим образом:

, (8)

где ₊ и _– — количество ионов А с зарядом z+ и ионов B c зарядом z–, на которые распадается исходная частица.

Для раствора электролита в целом можно записать:

_соли = ⁰_соли + RT·ln a_соли, (9)

С другой стороны химический потенциал электролита складывается из химических потенциалов ионов, так как электролит распадается на ионы:

_соли = _ _ + _ _, (10)

₊ и _ относятся к одному молю ионов, _соли – к одному моль электролита. Подставим выражение (10) в (9):

_ _ + _ _ = ⁰_соли + RT ln a_соли (11)

Для каждого типа ионов можем записать уравнение типа (9):

 _ = ⁰_ + RT·ln a_

 _ = ⁰_ + RT·ln a_ (12)

Подставим уравнение (12) в левую часть уравнения (11) и поменяем местами правую и левую части.

⁰_с + RT·ln a_с = _ ⁰_ + ₊RT·ln a_ + _– ⁰_– + _ RT·ln a_ (13)

Объединим все слагаемые с ⁰ в левой части

(⁰_с - _ ⁰_ - _ ⁰_ ) = _ RT·ln a_ + _ RT·ln a_  RT·ln a_соли (14)

Если учесть, что по аналогии с формулой (10)

⁰_С = _ ⁰_ + _ ⁰_ (15)

то ⁰_С - _ ⁰_ - _ ⁰_ = 0 (16)

Уравнение (15) аналогично уравнению (10), но оно относится к стандартному состоянию, когда (а_С = а₊ = а_- = 1). В уравнении (14) правая часть равна нулю, и оно перепишется следующим образом:

RT·ln a_с = _ RT·ln a_ + _ RT·ln a_

ln a_с = ln a_^ + ln a_^

, (17)

Это связь активности электролита в растворе с активностями ионов

где а_С — активность электролита, а₊ и а_– — активности положительных и отрицательных ионов. Например, для бинарных электролитов АВ справедливо:

, следовательно

Нельзя принципиально найти экспериментально активности отдельных ионов, т.к. нужно было бы иметь дело с раствором из одного вида ионов. Это невозможно. Поэтому было введено понятие средней ионной активности (), представляющей собой среднее геометрическое из активности отдельных ионов:

, где . (18)

или подставив выражение (17) имеем:

, (19)

Криоскопический метод и метод, основанный на определении давления пара, позволяют определить активность электролита в целом (а_С) и по уравнению (19) найти среднюю ионную активность.

Во всех случаях, когда возникает необходимость подстановки величины а₊ или а_– в какое-то уравнение, эти величины заменяют средней активностью данного электролита а_, например,

а_  а₊  а_–

Как известно, активность связана с концентрацией соотношением a=f∙m. Средний ионный коэффициент активности () определяется выражением, аналогичным выражению для средней ионной активности

. (20)

Существуют табличные значения для различных способов выражения концентраций (моляльность, молярность, мольные доли). Для них имеет численно разные значения. Экспериментально значения определяют криоскопическим методом, методом измерения давления пара, методом измерения ЭДС гальванических элементов и др.

Аналогично средний ионный стехиометрический коэффициент _ определяется из выражения

(21)

Средняя ионная моляльность () определяется как

. (22)

Если концентрацию раствора выражать через моляльность, то

.

и, подставив выражения

m₊=ν₊m, m_-=ν_-m,

где m   моляльность раствора, будем иметь

. (23)

Пример 7.1. Найти связь между активностью электролита, его моляльной концентрацией и средним ионным коэффициентом активности для растворов NaCl и Na₂CO₃ моляльности m.

а) Концентрации ионов, образующихся при полной диссоциации NaCl, равны m:

.

Так как ₊ = _– = 1, то

.

Для равновалентных электролитов средняя моляльность будет равна общей моляльности электролита:

.

Тогда

,

.

б) Концентрации ионов, образующихся при полной диссоциации Na₂CO₃, равны

.

Так как ₊ = 2, _– = 1, то .

,.
7.3. Понятие об электростатической теории сильных электролитов Дебая-Гюккеля. Правило ионной силы.
Средний ионный коэффициент активности зависит от концентрации раствора, эта зависимость показана на рис. 3. В области предельно разбавленных растворов электролитов эта зависимость имеет линейный характер в координатах .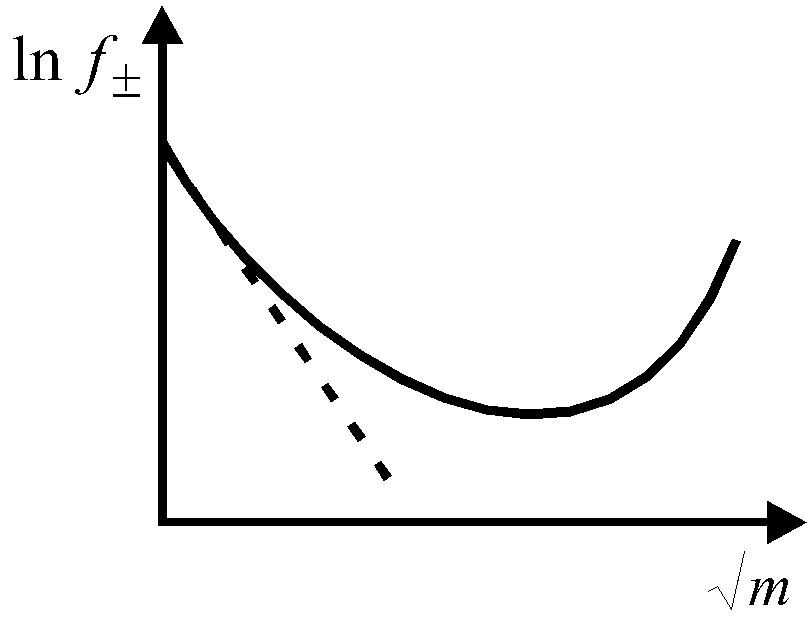




Рис. 3. Зависимость среднего коэффициента активности ионов

от концентрации электролита
Присутствие в растворе других солей изменяет коэффициент активности данной соли и тем сильнее, чем больше заряд добавляемых ионов. Суммарное действие всех ионов в растворе выражается через ионную силу раствора ,

, (24)

где m_i – концентрация i-ого иона; z_i – заряд i-ого иона.

Зависимость среднего коэффициента активности ионов от ионной силы раствора имеет также аналогичный сложный характер и представлена на рис. 4.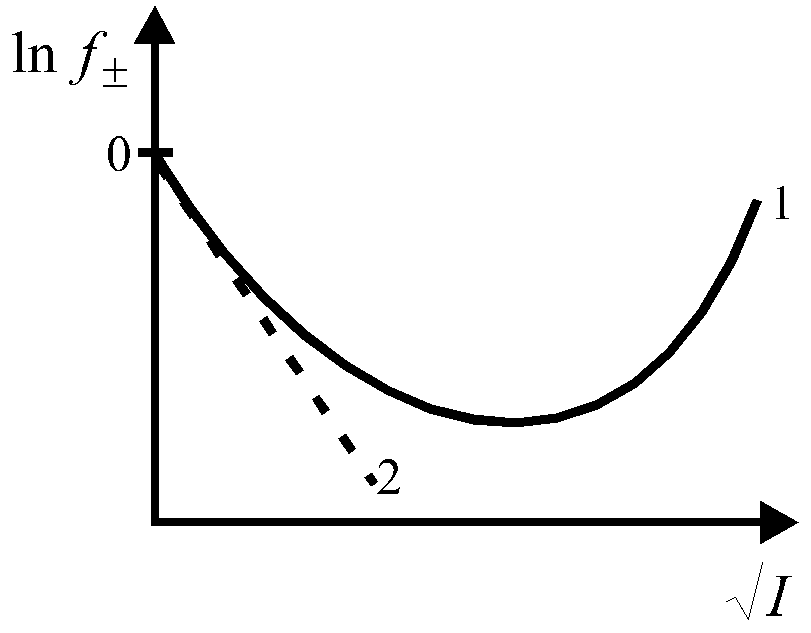



Рис. 4. Зависимость среднего коэффициента активности от ионной силы раствора.

Пример 2. Определить ионную силу раствора, содержащего на 1000 г воды 0,01 моль и 0,1 моль .

Решение. Ионная сила такого раствора равна





Пример 3. Определить ионную силу раствора с моляльностью m = 0,5.

Решение. По уравнению (7.16) получаем

.
Для растворов сильных электролитов выполняется правило ионной силы: в растворах с одинаковой ионной силой средние коэффициенты активности ионов равны.

Для теоретического расчета значений коэффициента активности f была предложена теория Дебая-Гюккеля. Она количественно учитывает ион-ионные взаимодействия и достаточно хорошо объясняет свойства разбавленных растворов сильных электролитов (=1).

В основе теории Дебая-Гюккеля лежат следующие предположения

1. 
   электростатическое взаимодействие противоположно заряженных ионов приводит к тому, что вокруг положительных ионов вероятность нахождения отрицательных ионов будет больше, чем положительных.
   
2. 
   между ионами имеет место кулоновское взаимодействие
   
3. 
   вокруг каждого иона формируется ионная атмосфера из противоположно заряженных ионов. (Сфера, в которой преобладает заряд, противоположный по знаку центральному иону среды, и называется ионной атмосферой).
   

Теория сильных электролитов приводит к следующему соотношению, связывающему средние коэффициенты активности ионов с ионной силой раствора в области сильно разбавленных электролитов:

, (25)

где A = f (ε, T) – константа, зависящая от диэлектрической проницаемости растворителя () и температуры (T).

Уравнение (25) применимо лишь при очень больших разведениях (I ≤ 0,01, рис. 4), почему и получило название предельного закона Дебая-Гюккеля.

Кривая 1 (рис. 4) описывает экспериментальную зависимость коэффициента активности от ионной силы раствора, кривая 2 описывает эту зависимость в соответствии с предельным законом Дебая-Гюккеля.

Для водных растворов бинарных электролитов при 25С справедливо:

. (26)