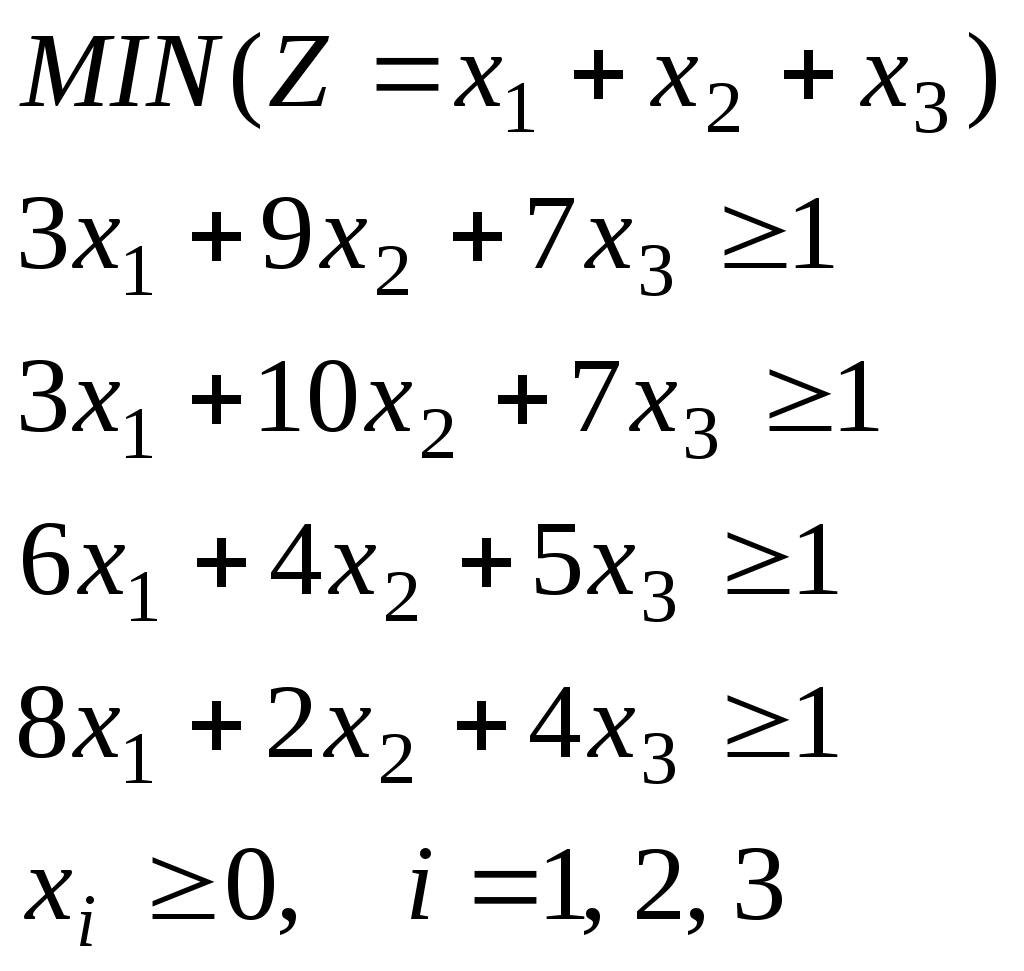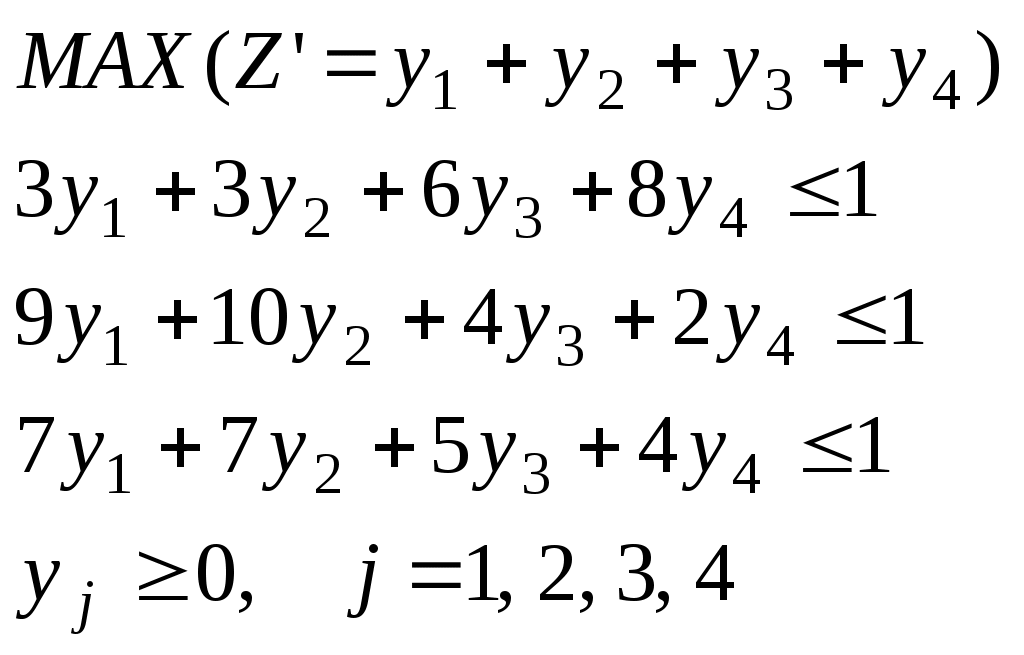Элементы теории игр. Лекция Элементы теории игр
 Скачать 192.5 Kb. Скачать 192.5 Kb.
|
|
\ Лекция «Элементы теории игр» Рассмотрим задачу. Предприятие может выпускать три вида продукции – A1, A2 и A3, получая при этом прибыль, зависящую от спроса, который может быть в одном из четырех состояний – B1, B2, B3, B4. Дана матрица, ее элементы aij характеризуют прибыль, которую получит предприятие при выпуске i-й продукции при j-м состоянии спроса.
Определить оптимальные объемы выпускаемой продукции, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным. Ознакомимся с основными понятиями теории игр. Математическая модель конфликтной ситуации называется игрой, стороны, участвующие в конфликте, – игроками, а исход конфликта – выигрышем. Для каждой формализованной игры вводятся правила, т.е. система условий, определяющая: 1) варианты действий игроков; 2) объем информации о поведении партнеров, которой владеет каждый игрок; 3) выигрыш, к которому приводит каждая совокупность действий. Как правило, выигрыш (или проигрыш) может быть задан количественно. Игра называется парной, если в ней участвуют два игрока, и множественной, если число игроков больше двух. Мы будем рассматривать только парные игры. В них участвуют два игрока: А и В, интересы которых противоположны, а под игрой будем понимать ряд действий со стороны игроков А и В. Игра называется игрой с нулевой суммой или антагонистической, если выигрыш одного из игроков равен проигрышу другого, т.е. для полного "задания" игры достаточно указать величину выигрыша первого игрока. Выбор и осуществление одного из предусмотренных правилами действий называется ходом игрока. Стратегией игрока называется совокупность принципов, определяющих выбор его действий при каждом личном ходе в зависимости от сложившейся ситуации. Игра называется конечной, если у каждого игрока имеется конечное число шагов. Для того чтобы найти решение игры, следует для каждого игрока выбрать стратегию, которая удовлетворяет условию оптимальности, т.е. один из игроков должен получать максимальный выигрыш, когда второй игрок придерживается своей стратегии. В то же время второй игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии. Такие стратегии называются оптимальными. Оптимальные стратегии должны также удовлетворять условию устойчивости, т.е. любому из игроков должно быть невыгодно отказаться от своей стратегии в этой игре. Целью теории игр является определение оптимальной стратегии для каждого игрока. При выборе оптимальной стратегии естественно полагать, что оба игрока ведут себя разумно с точки зрения своих интересов. Матрица, элементы которой характеризуют прибыль первого игрока при всех возможных стратегиях, называется платежной матрицей игры. Рассматриваемая задача сводится к игровой модели, в которой игра предприятия А против спроса В задана платежной матрицей
Обозначим через ai наименьший выигрыш игрока А при выборе им стратегии А. для всех возможных стратегий игрока В (наименьшее число в i-й строке платежной матрицы), т.е. ai = min aij. Среди всех чисел ai (i = 1, 2, ..., m) Выберем наибольшее: α = max αi. Назовем α нижней ценой игры или максимальным выигрышем (максими-ном). Это гарантированный выигрыш игрока А при любой стратегии игрока В. Следовательно, α = max min aij. Стратегия, соответствующая максимину, называется максиминной стратегией. Игрок В заинтересован в том, чтобы уменьшить выигрыш игрока А. Выбирая стратегию Bj, он учитывает максимально возможный при этом выигрыш для игрока А. Обозначим βj = max aij Среди всех чисел βj выберем наименьшее: β = min βj и назовем β верхней ценой игры или минимаксным выигрышем. Это гарантированный проигрыш игрока В. Следовательно, β = min max aij. Стратегия, соответствующая минимаксу, называется минимаксной стратегией. Принцип, диктующий игрокам выбор наиболее "осторожных" минимаксной и максиминной стратегий, называется принципом минимакса. Этот принцип следует из разумного предположения, что каждый игрок стремится достичь цели, противоположной цели противника. Определим нижнюю и верхнюю цену игры и соответствующие стратегии в задаче: α = 4, β = 6. Так как Смешанной стратегией SA игрока А называется применение чистых стратегий A1, A2, …, Ai, …, Am c вероятностями p1, p2, …, pi, …, pm, причем сумма вероятностей равна 1: сываются в виде строки SA = (p1, p2, …, pi, …, pm). Аналогичн смешанные стратегии игрока В обозначаются в виде строки SB = (q1, q2, …, qi, …, qm), где сумма вероятностей появления стратегий равна 1: Итак, SA* = (p1, p2, p3) и SB*= (q1, q2, q3, q4). Обозначив xi = pi /v, i= 1, 2, 3, 4 и yj = pj,/v, j = 1, 2, 3, 4, составим пару двойственных задач линейного программирования, затем приведем математическую модель задачи к каноническому (стандартному) виду и решим симплексным методом .Из симплексной таблицы с оптимальным решением возмем значения параметров (-Z), xi и вычислим цену игры v, и вероятности применения стратегий pi. Сделать анализ решения.
Игры с « природой». Для того чтобы можно сделать вывод о том какую именно стратегию выбирать игроку, необходимо использовать критерии Вальда, Гурвица, Сэвиджа, Лапласа, Байеса. 1. Критерий Вальда. Рекомендуется применять максиминную стратегию. Она достигается из условия maxminαij и совпадает с нижней ценой игры. ji Критерий является пессимистическим, считается, что природа будет действовать наихудшим для человека образом, агрессивно, делать все, чтобы помешать нам достигнуть успеха. Рассмотрим задачу. Ежедневный спрос на булочки в продовольственном магазине может принимать следующие значения
Если булочка не продана днем, то она м.б. реализована за 15 центов к концу дня. Свежие булочки продаются по 49 центов за штуку. Затраты магазина на одну булочку 25 центов. Используя игровой подход, определить, какое число булочек надо заказывать ежедневно. Составим платежную матрицу. Сначала вычислим прибыль (49-25=24) и убыток (15-25=-10).
Платежная матрица примет вид
Вычислим критерий Вальда - максиминный. Он отражает принцип гарантированного результата: Олицетворяет позицию крайнего пессимизма: надо ориентироваться всегда на худшие условия, зная наверняка, что хуже этого не будет. Этот перестраховочный подход для того, кто очень боится проиграть. Оптимальной считается стратегия, при которой гарантируется выигрыш в любом случае, не меньший, чем нижняя цена игры с природой: Н = max minαij j i Подсчитать min по строкам и выбрать ту стратегию, при которой минимум строки максимален.
Критерий Вальда рекомендует выбирать стратегию А1. 2. Критерий Гурвица (оптимизма - пессимизма). Критерий рекомендует при выборе решения не руководствоваться ни крайним пессимизмом (всегда рассчитывай на худшее), ни крайним легкомысленным оптимизмом (авось кривая выведет). Критерий рекомендует стратегию, определяемую по формуле H = Max {γmin aij + (1- γ)max aij} j i i где γ - степень оптимизма - изменяется в диапазоне [0, 1]. Критерий придерживается некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего поведения природы. При γ = 1 критерий превращается в критерий Вальда, при γ = 0 - в критерий максимума. На γ оказывает влияние степень ответственности лица, принимающего решение по выбору стратегии. Чем хуже последствия ошибочных решений, больше желания застраховаться, тем γ ближе к единице. Рассмотрим платежную матрицу. Параметр Гурвица возьмем равным 0,6.
Критерий Гурвица рекомендует стратегию А5. 3. Критерий Сэвиджа. Суть критерия состоит в выборе такой стратегии, чтобы не допустить чрезмерно высоких потерь, к которым она может привести. Находится матрица рисков, элементы которой показывают, какой убыток понесет человек (фирма), если для каждого состояния природы он не выберет наилучшей стратегии. Элементы матрицы рисков находится по формуле (rij): rij = max aij - aij где max aij - максимальный элемент в столбце исходной матрицы. j Оптимальная стратегия находится из выражения H = Min {max(max aij - aij)} j i j Составим матрицу риска, (maxaij- aij). Выберем максимальный элемент в столбце и вычитаем из него остальные элементы столбца, получим max(max aij - aij).
Из максимальных значений последнего столбца выбираем минимальную величину, получим Min {max(max aij - aij)}. Критерий Сэвиджа рекомендует стратегию А4. 4. Критерий Лапласа. Этот критерий основывается на принципе недостаточного обоснования. Поскольку вероятности состояния не известны, необходимая информация для вывода, что эти вероятности различны, отсутствует. Поэтому можно предположить, что они равны. Выбор стратегии осуществляется по формуле H = Max {1/n·∑ aij} где 1/n вероятность реализации одного из состояний р = 1/n.
Критерий Лапласа рекомендует нам стратегию А4. Таким образом, рассмотрев одну платежную матрицу, мы получили, что критерии Лапласа и Сэвиджа рекомендует стратегию А4. То есть необходимый заказ булочек составит 250 единиц ежедневно. 5. Критерий Байеса. Принятие решения в условиях риска. Если в рассмотренных выше критериях, необходимая информация о вероятностях какого-либо состояния отсутствовала, то критерий Байеса действует в условиях не полной информации, т.е. в условиях риска (имеется информация о вероятностях применения стратегий второй стороной). Эти вероятности называются априорными вероятностями. Выбор стратегии осуществляется по формуле H = Max {∑pi aij} Ежедневный спрос на булочки в продовольственном магазине задается следующим распределением вероятностей
Поставив значение aij и pi в формулу, получим:
Критерий Байеса рекомендует стратегию А3 В условиях полной неопределенности теория не дает однозначных принципов выбора того или иного критерия. Оптимальные стратегии, выбранные по различным критериям, различны. Таким образом, окончательный вывод зависит от предпочтений человека, который принимает решение. ПРИМЕР №1 Найти оптимальные стратегии 1-го игрока, исходя из различных критериев, в игре с полной неопределенностью относительно второго игрока, заданной платежной матрицей:     а11 а12 а13 а14 5 10 18 25 а11 а12 а13 а14 5 10 18 25 а21 а22 а23 а24 8 7 8 23 А = а31 а32 а33 а34 ; А = 21 18 12 21 а41 а42 а43 а44 20 22 19 15 Решение. 1. Максиминный критерий Вальда.Н = maxmin аij ji Вычислим минимальные значения по строкам min аij, а далее из них выберем максимальное.   5 10 18 25 5 А = 8 7 8 23 7 21 18 12 21 12 20 22 19 15 15 Таким образом, получаем Н = maxmin аij = 15 при применении стратегии А4. ij Ответ: оптимальной стратегией 1-го игрока А является стратегия А4. 2. Критерий Гурвица. Параметр Гурвица возьмем равным γ=0,6: H = Max {γmin aij + (1- γ)max aij} j i i   5 10 18 25 5 25 5*0,6+0,4*25=13 А = 8 7 8 23 7 23 7*0,6+0,4*23=13,4 21 18 12 21 12 18 12*0,6+0,4*18=14,4 20 22 19 15 15 22 15*0,6+0,4*22=17,8 Получаем H = max[0.6 min аij+(1-0.6) max аij]=17.8 jii Ответ: оптимальной стратегией первого игрока является стратегия А4. 3. Критерий Сэвиджа (критерий минимаксного риска). Необходимо построить матрицу рисков. Для этого: 1) вычислить максимальные значения по столбцам   5 10 18 25 5 10 18 25А = 8 7 8 23 21 18 12 21  20 22 19 15 20 22 19 15 21 22 19 25 2) вычислить матрицу рисков: rij= max аij- аij     21-5 22-10 19-18 25-25 16 12 1 0 rij= 21-8 22-7 19-8 25-23 = 13 15 11 2 21-21 22-18 19-12 25-21 0 4 7 4 21-20 22-22 19-19 25-15 1 0 0 10 3) вычислить максимальные значения по строкам и из них выберем строку с минимальным значением:   16 12 1 0 16 16 12 1 0 16 13 15 11 2 15 rij= 0 4 7 4 7 1 0 0 10 10 Получаем H = min maxrij = 7 при применении стратегии А3. ij Ответ: оптимальной стратегией первого игрока является стратегия А3. 4. Критерий Лапласа. n Вычислить средние арифметические по строкам [1/n ∑ аij]   5 10 18 25 0.25 (5+10+18+25)=14.5 j=1 5 10 18 25 0.25 (5+10+18+25)=14.5 j=1 A = 8 7 8 23 0.25 (8+7+8+23)=11.5 21 18 12 21 0.25 (21+18+12+21)=18 20 22 19 15 0.25 (20+22+19+15)=19 n Получаем H = max[1/n ∑ аij] =19 при применении стратегии А4. i j=1 Ответ: оптимальной стратегией первого игрока является стратегия А4. Выбор стратегии в условиях риска (при наличии вероятностной информации).  В1 В2 В3 В4 n В1 В2 В3 В4 n А1 5 10 18 25 H = max∑Pj аij А1 5 10 18 25 H = max∑Pj аijА2 8 7 8 23 j j=1 А3 21 18 12 21 А4 20 22 19 15 Вероятности стратегий второго игрока.
5*0.2+10*0.15+18*0.35+25*0.3=16.30 8*0.2+7*0.15+8*0.35+23*0.3=12.35 21*0.2+18*0.15+12*0.35+21*0.3=17.40 20*0.2+22*0.15+19*0.35+15*0.3=18.45 Получаем Н = 18,45 при применении стратегии А4. Ответ: оптимальной стратегией первого игрока является стратегия А4. ПРИМЕР №2 Предприятие имеет возможность самостоятельно планировать объемы выпуска сезонной продукции А1, А2, А3. Не проданная в течении сезона продукция позже реализуется по сниженной цене. Данные о себестоимости продукции, отпускных ценах и объемах реализации в зависимости от уровня спроса приведены в таблице:
Требуется: 1) придать описанной ситуации игровую схему, указать допустимые стратегии сторон, составить платежную матрицу 2) дать рекомендации об объемах выпуска продукции по видам, обеспечивающих предприятию наивысшую прибыль. Указание. Для уменьшения размерности платежной матрицы считать, что одновременно на все три вида продукции уровень спроса одинаков: повышенный, средний или пониженный.
Решение. В игре участвуют 2 игрока: А - производитель, В - потребитель. Игрок А стремится реализовать свою продукцию так, чтобы получить максимальную прибыль. Стратегиями игрока А являются: А1 - продавать продукцию при повышенном состоянии спроса (a1= 14 , a2 =38 , a3 =24), А2 - продавать продукцию при среднем состоянии спроса (a1= 8 , a2 =22 , a3 =13), А3 - продавать продукцию при пониженном состоянии спроса (a1= 5 , a2 =9 , a3 =7), Игрок В стремится приобрести продукцию с минимальными затратами. Стратегиями игрока В являются: В1 - покупать продукцию при повышенном состоянии спроса (14 +38+24), В2 - покупать продукцию при среднем состоянии спроса (8+22+13), В3 - покупать продукцию при пониженном состоянии спроса (5+9+7). Интересы игроков А и В - противоположны. Определим цену продукции в течение сезона и после уценки:
Рассчитаем элементы платежной матрицы
Платежная матрица примет вид
α = max αi = 17.6 β = min βj = 17.6 Так как α = β = ν = 17,6, то найдена седловая точка. Значит оптимальное решение: А3; В3 Производитель (игрок А) получит гарантированную прибыль в размере 17,6 ден.ед., если будет реализовывать свою продукцию при пониженном уровне спроса в объеме 5,9 и 7 ед. соответственно продукции а1, а2 и а3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||