Лекция магниты. Лекция Магнитные явления. Переменный ток для ОЗО. Лекция магнитное поле . Магнитное взаимодействие электрических токов

• Название: Лекция магнитное поле . Магнитное взаимодействие электрических токов
• Анкор: Лекция магниты
• Дата: 03.06.2022
• Размер: 2.07 Mb.
• Имя файла: Лекция Магнитные явления. Переменный ток для ОЗО.doc
• Тип: Закон; #567080
• страница: 2 из 5

§ 14. Действие магнитного поля на токи и движущиеся заряды

1 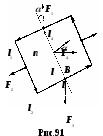. Прямолинейный ток в однородном магнитном поле. Как уже говорилось в §13, на элемент тока Idl, в однородном магнитном поле с индукцией B действует сил Ампера . Если элемент тока имеет постоянную величину Il, а магнитное поле в пределах его однородно, то сила Ампера принимает вид (рис.90): . (14.1)

2. Замкнутый контур с током в однородном магнитном поле. Найдём силы, действующие на прямоугольную рамку с током (рис.91). Полагаем, что по рамке в направлении стрелок течёт постоянный ток I.

Силы F₂ и F₄, приложенные к элементам тока Il₂ и Il₄, действуют в плоскости рамки в разные стороны, то есть просто растягивают рамку. Силы F₁и F₃ образуют пару сил. Как известно из механики, крутящий момент пары равен векторному произведению отрезка l, проведённого из точки приложения одной силы F₂ в точку приложения к другой F₁, на силу F₁.

Если в нашем случае в качестве такого отрезка взять сторону рамки l₄, то момент пары . (14.2)

Но сила . Отсюда . В круглых скобках заключены скалярные произведения векторов. Так как рамка имеет по условию прямоугольную форму, то l₁l₄. Поэтому второе слагаемое равно нулю, . По определению скалярного произведения . . (14.3)

Если ввести единичный вектор нормали n, ориентированный по току рамки правилом правого винта, то .

Вектор представим как произведение его модуля l₁ на единичный вектор , . Приняв во внимание, что  площадь рамки, получаем:

. (14.4)

Здесь - магнитный момент рамки с током.

В полученной формуле нет геометрии рамки. Поэтому выражение (14.4) применимо к рамкам с током любой формы. Необходимым условием для определения момента M является значение магнитного момента p_m и его ориентации относительно поля B.

Р 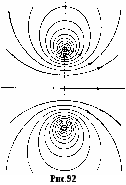амка с током в магнитном поле испытывает действие вращающего момента подобно диполю в электрическом поле, для которого . Контур с током стремится повернуться во внешнем поле так, чтобы его магнитный момент совпадал по направлению с внешним полем B. Поэтому поле вблизи оси контура усиливается, .

Поле контура вне его на достаточно большом удалении от оси практически незаметно и потому не ослабляет внешнего поля (рис.92).

Если вносить в магнитное поле систему свободно ориентирующихся в пространстве контурных токов, то вследствие их единой ориентации по внешнему полю это поле усиливается.

Для сравнения: электрическое поле в диэлектриках ослабляется по сравнению с вакуумом.

По аналогии с электрическим диполем рамку с током называют часто магнитным диполем.

Е 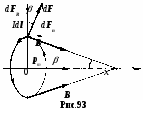сли магнитный момент p_m рамки с током сонаправлен с внешним полем, p_mB, вращающий момент M равен нулю, а силы Ампера стремятся растянуть рамку. Если p_mB, то силы Ампера стремятся сжать рамку.

3. Замкнутый контур с током в неоднородном магнитном поле. Рассмотрим круговой виток с током в неоднородном магнитном поле, когда p_mB, а поле B симметрично относительно оси витка.

Пусть ОХ  ось витка. Будем полагать, что внешнее магнитное поле усиливается вдоль оси ОХ, его линии B сближаются (рис.93).

На любой элемент тока Idl действует сила Ампера . Эта сила перпендикулярна вектору B и может быть разложена на две составляющие: dF_R, параллельную плоскости рамки и растягивающую её (или сжимающую, когда p_mB,) и dF_n, нормальную плоскости рамки. Эта сила втягивает рамку в поле большей индукции (p_mB) или выталкивает её (p_mB).

Угол между элементом тока Idl и вектором B во всех точках контура равен 90. Поэтому dF = IdlB, а dF_n = dFsinn = IBsinndl.

Здесь n- единичный вектор нормали площадки контура, он совпадает по направлению с вектором магнитного момента, np_m.

Сила F_n, действующая вдоль оси OX на весь контур, найдётся интегрированием.

. (14.5)

Здесь p_m = IR²n  магнитный момент контура.

Угол  - промежуточный параметр. Он определятся скоростью изменения индукции B вдоль оси ОХ. Исключим его. Из условия неразрывности линий магнитной индукции B, когда , для двух сечений, расположенных на расстоянии dx друг от друга (рис.94), получаем: . (14.6)

Раскрываем скобки: .

Пренебрегаем величинами 2 и 3 порядков малости. Тогда (14.7)

Подставляем в формулу (14.5) вместо 2BR выражение (14.7), приняв во внимание, что dRdx = tg. . (14.8)

Здесь B_n = Bcos - проекция вектора индукции на ось контура ОХ, иначе, нормальная к контуру составляющая вектора B.

И 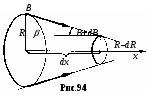так, на рамку с током в однородном магнитном поле действует только вращающий момент M, стремящийся развернуть рамку в устойчивое положение, когда p_mB.

На рамку с током в неоднородном магнитном поле кроме вращающего момента M действует ещё сила вдоль линий поля. Направление силы зависит от взаимной ориентации векторов B и p_m. Если p_mB или, по крайней мере, угол p_mB<2, рамка втягивается в поле более высокой напряжённости. Если угол p_mB>2, рамка выталкивается из поля.

Когда речь идёт об атомных токах, то в статистике, если бы атомные токи были жёстко ориентированы в пространстве, втягивающие силы уравновешивались бы выталкивающими. Но поскольку каждый атомный ток испытывает ещё действие вращающего момента M, стремящегося развернуть атом в положение, когда p_mB, то втягивающая сила преобладает над выталкивающей. Поэтому тела, у которых магнитные моменты атомов не равны нулю, p_m  0(парамагнетики), всегда втягиваются в область поля с более высокой индукцией.

Чем быстрее изменяется поле, тем больше величина dBdx, тем больше втягивающая или выталкивающая сила.

4. Действие магнитного поля на движущийся электрический заряд. Поскольку магнитное поле действует только на проводник с током, логично заключить, что действие магнитного поля на проводник обусловлено действием поля на движущиеся заряды. Найдём силу действия магнитного поля на движущийся заряд.

Ток в проводнике I = jS = envS, где e - величина движущегося заряда, n - концентрация зарядов, v - средняя скорость их дрейфа.

Сила Ампера действия магнитного поля на ток . (1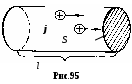4.9)

З десь l вектор длины отрезка проводника, направленный по току, S  сечение проводника (рис.95). Вектор l совпадает по направлению с вектором скорости и дрейфа положительных зарядов. Поэтому в формуле (14.9) величины l и v можно поменять местами. . (14.10)

Произведение nlS = N представляет собой число зарядов в объёме проводника. Разделив силу Ампера на число N движущихся в проводнике зарядов, получаем силу действия магнитного поля на отдельный движущийся заряд. . Сила Лоренца (14.11)

Формулу (14.11) получил в 90-х годах XIX в. Хендрик Лоренц в рамках классической электронной теории проводимости металлов.

Если в пространстве кроме магнитного поля есть ещё и электрическое, то на движущийся заряд e действуют две силы. . (14.12)

Сила Лоренца (14.11) всегда направлена по нормали к скорости v. Поэтому она изменяет скорость движения частицы только по направлению, но не по величине. Поэтому и кинетическая энергия заряженной частицы, движущейся со скоростью v << c в магнитном поле постоянной индукции B, остаётся практически неизменной.

Сила Лоренца не совершает работы, поэтому её относят к группе гироскопических сил.

5. Движение заряженной частицы в магнитном поле, когда vB. Пусть положительно заряженная частица с зарядом e влетает в однородное магнитное поле перпендикулярно его силовым линиям, т.е. vB. Из формулы (14.11) следует, что fB. Ускорение частицы, вызываемое силой Лоренца, также перпендикулярно B. Поэтому движение частицы происходит по окружности в плоскости, перпендикулярной B (рис.96).

Р 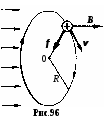адиус окружности R найдётся из условия: , . (14.13)

Величина радиуса тем больше, чем больше импульс частицы mv и чем меньше индукция поля B.

Движение заряженных частиц в магнитных полях теоретически исследовал в 1895 г. Джозеф Лармор. Поэтому окружность, по которой движется заряженная частица в магнитном поле, называют часто ларморовской окружностью.

Зная радиус ларморовской окружности, описываемой частицей, можно найти период обращения частицы.

. (14.14)

Период T ларморовского вращения заряженных частиц в магнитном поле не зависит от скорости их движения (иначе, от кинетической энергии), а определяется лишь индукцией магнитного поля B и удельным зарядом частиц em. Это обстоятельство играет важную роль в практике создания ускорителей заряженных частиц. Частота называется циклотронной частотой вращения. (14.15)

6. Движение заряженной частицы в магнитном поле, когда скорость v не перпендикулярна B. Если частица влетает в магнитное поле так, что её скорость v образует с вектором B угол, не равный 90, то траекторией движения частицы является винтовая линия (рис.97).

С 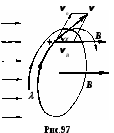оставляющая скорости v_n, перпендикулярная линиям B, закручивает частицу по окружности радиуса R = mv_neB. Касательная составляющая v_B, параллельная линиям B, смещает частицу вдоль поля. Поэтому траектория частицы как бы навивается на линии магнитного поля. Шаг винтовой линии . (14.16)

Если угол между векторами v и B равен , то v_B = vcos , v_n = vsin.

В 1950 г. Игорь Тамм и Андрей Сахаров предложили использовать кольцевое поле в тороиде для удержания плазмы от размывания.

П 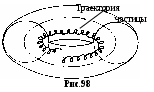лазмой называют газ из электрически заряженных частиц. В холодной плазме (температура не более 210⁴ K) такими частицами являются электроны, ядра атомов и ионизированные атомы. В горячей плазме (T  210⁴ K) присутствуют только электроны и ядра. Необходимость сохранять в течение какого-то времени в замкнутом пространстве столь горячее вещество появилась при решении проблемы управляемого термоядерного синтеза.

З апускаемые под углом к оси тороида с магнитным полем заряженные частицы движутся по траекториям, которые навиваются на замкнутые силовые линии поля в тороиде (рис.98). В результате плазма в течение какого-то времени удерживается от размывания и от охлаждения.

7. Зеркальные магнитные ловушки. В 1952 г. Герш Будкер и Ричард Пост предложили для удержания плазмы зеркальную магнитную ловушку. Она представляет собой осесимметричное магнитное поле, образованное двумя однонаправленными кольцевыми токами 1 и 2 с общей осью (рис.99). Области максимальной индукции магнитного поля, находящиеся в плоскостях этих кольцевых токов, называются магнитными пробками.

При движении частицы в область более сильного поля скорость движения её по окружности v_n увеличивается, а скорость смещения её вдоль линий поля v_B уменьшается. В какой-то точке поля составляющая v_B обращается в нуль. Здесь происходит отражение частицы от магнитного зеркала. В результате частица дрейфует от одной пробки к другой.

8 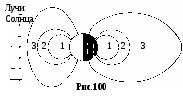. Радиационные пояса Земли. Примером ловушки зеркального типа является магнитное поле Земли с магнитными пробками на полюсах (рис.100).

Частицы солнечного ветра – протоны и электроны – попадая в магнитное поле Земли, удерживаются им и образуют радиационные пояса. Большая доля частиц движутся как бы навиваясь под действием силы Лоренца на магнитные силовые линии Земли, дрейфуя от одного полюса до другого. В близи полюсов происходит их отражение (5 на рис.100).

Расстояние от полюса до полюса частица проходит за время примерно 0,3 c. Протон в такой геомагнитной ловушке может удерживаться до 100 лет.

В поясах существует динамическое равновесие. Внутри поясов частицы уходят из-за торможения, а их убыль компенсируется частицами, приходящими из космоса.

Радиационные пояса Земли были открыты в 1958 г. с помощью искусственных спутников Земли. Оказалось, что существуют два электронных пояса и одни протонный, в значительной степени перекрывающиеся между собой. Внутренний электронный 1 и протонный 2 начинаются примерно на одной высоте 1000 км над поверхностью Земли. Максимум концентрации протонного пояса 2 удалён от центра Земли примерно на три земных радиуса 3R. Энергия протонов меняется от 40 МэВна внутренней границе пояса до 0,5 МэВна внешней.

Максимум концентрации внутреннего электронного пояса 1 удалён от центра Земли на 1,5 МэВ, а максимум концентрации внешнего электронного пояса 3 – на 5R (рис.100).