Лекция магниты. Лекция Магнитные явления. Переменный ток для ОЗО. Лекция магнитное поле . Магнитное взаимодействие электрических токов

• Название: Лекция магнитное поле . Магнитное взаимодействие электрических токов
• Анкор: Лекция магниты
• Дата: 03.06.2022
• Размер: 2.07 Mb.
• Имя файла: Лекция Магнитные явления. Переменный ток для ОЗО.doc
• Тип: Закон; #567080
• страница: 5 из 5

§. Электрические колебания в колебательном контуре. Колебательные системы.

1. Свободные затухающие колебания. Колебательным контуром называется цепь, содержащая ёмкость С и индуктивность L. Реальный контур всегда имеет некоторое активное (омическое) сопротивление R (рис.150).

Если зарядить конденсатор, а затем замкнуть ключ Кл, то конденсатор будет разряжаться через катушку L, в цепи контура пойдёт ток i = dqdt, где q – заряд на конденсаторе. Чтобы определить зависимость тока от времени (или заряда на обкладках конденсатора), полагаем цепь квазистационарной и составим 2-е правило Кирхгофа для контура: iR = U_C + E. Здесь U_C = qC – напряжение на обкладках конденсатора, E  ЭДС индукция в катушке. При обходе по часовой стрелке на рис.150 получаем: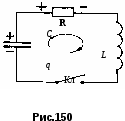

, или . (21.1)

Знак “минус” перед напряжением на конденсаторе qC ставится потому, что ход потенциала на конденсаторе при обходе по контуру противоположен ходу потенциала на резисторе. Обозначив RL = 2, 1CL =  , а в производных перейдя к точкам, получаем: . (21.2)

Это дифференциальное уравнение затухающих колебаний. Вид его решения зависит от соотношения между коэффициентами n и ₀. Если ₀ > 2n, колебания периодические затухающие, если ₀ < 2n, то колебания апериодические.

а 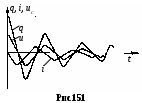. Периодические затухающие колебания. Будем полагать, что затухание очень слабое, так что ₀ >> 2n. Уравнение (21.2) такое же, как уравнение затухающих колебаний материальной точки. Его подробное решение см.[2], §124, с.с.553-556. Опустив выкладки, запишем приближённое решение уравнения 21.2 для заряда, тока и напряжения.

q = q₀e^-ntcost, (21.3)

i = q₀  e^-ntcos(t + /2), (21.4)

. Здесь . (21.5)

Графики q(t), i(t) и u_C(t) показаны на рис.151. При малых затуханиях период колебаний в контуре определяется формулой Томсона, . (21.6)

Декремент затухания . (21.7)

Логарифмический декремент затухания . (21.8)

Величина  волновое сопротивление контура,  добротность. (21.9)

У колебательных контуров среднего качества Q  20  100.

В идеальном контуре, в котором отсутствует затухание, R = 0, колебания должны продолжаться бесконечно долго. При этом максимальная энергия конденсатора , а 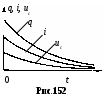максимальная энергия поля катушки составляет . Когда конденсатор максимально заряжен, i = 0, , вся энергия колебаний заключена в электрическом поле. Когда конденсатор разряжен, u = 0, а ток максимален. Вся энергия контура заключена в магнитном поле катушки. Средние и максимальные энергии электрического и магнитного полей одинаковы, . Однако колебания в любом реальном контуре даже из сверхпроводящих материалов обязательно затухают. Это происходит потому, что контур с переменным током излучает электромагнитные волны, которые уносят запасённую в нём энергию. В дифференциальном уравнении эти потери не учтены.

б . Апериодические колебания происходят при n > ₀. Если n >> ₀ и в цепи контура нет внешних ЭДС, то колебания представляют собой простой разряд конденсатора на выскоомный резистор. Заряд, напряжение на конденсаторе и ток изменяются в этом случае по экспоненциальному закону (рис.152):

(21.10)

Здесь . Из равенства n = ₀ находим критическое сопротивление контура, разделяющее периодические колебания от апериодических. n = ₀, ,  . (21.11)

Если сопротивление резистора R больше удвоенного волнового сопротивления  периодические колебания в контуре не возникают.

2 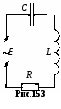. Вынужденные колебания возникают тогда, когда в контуре действует внешняя переменная ЭДС (рис.153). В отличие от подобного случая в цепи переменного тока, рассмотренного в §20, п.7, здесь полагаем, что диапазон частот, генерируемых внешним источником, много шире, а внутреннее сопротивление источника внешней ЭДС много больше.

Если в контуре действует периодическая ЭДС E =E_acost, то уравнение колебаний электрического заряда на обкладках конденсатора принимает вид: . (21.12)

Здесь те же обозначения: 2n = RL, .

Решение этого уравнения состоит из двух членов и при n << ₀ имеет вид: q = q₀e^ntcost + Bcos(t  ). (21.13)

Первый член описывает собственные затухающие колебания в контуре, рассмотренные в предыдущем пункте. Спустя некоторое время (не более нескольких секунд). Эти колебания практически исчезают. Остаётся лишь вторая часть, описывающие вынужденные колебания q = Bcos(t  ). (21.14)

Здесь B – амплитуда вынужденных колебаний,  - угол сдвига по фазе по отношению к собственным колебаниям. 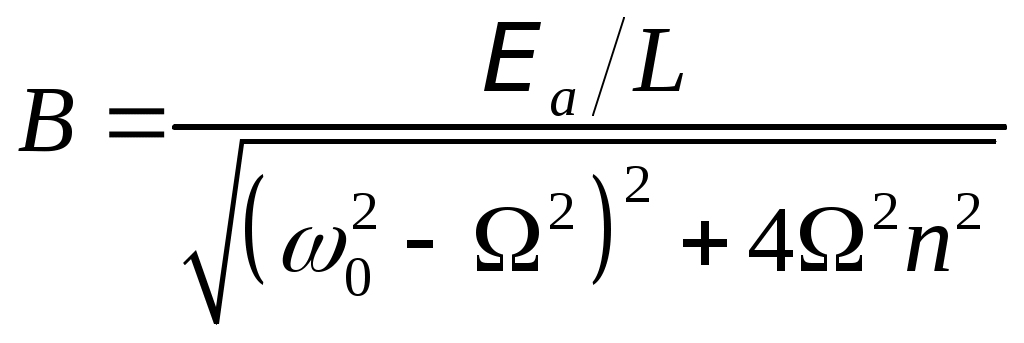, . (21.15)

Дифференцируя (21.14) по времени, получаем ток в контуре.

i = =  Bsin(t  ) = Bcos(t   + 2). (21.16)

Величина В = i_a есть амплитудный ток. Он зависит от соотношения частот ₀ и . Если частота  изменения внешней ЭДС приближается к частоте ₀ собственных затухающих колебаний, то ток в контуре возрастает до некоторого максимального значения, называемого резонансным. 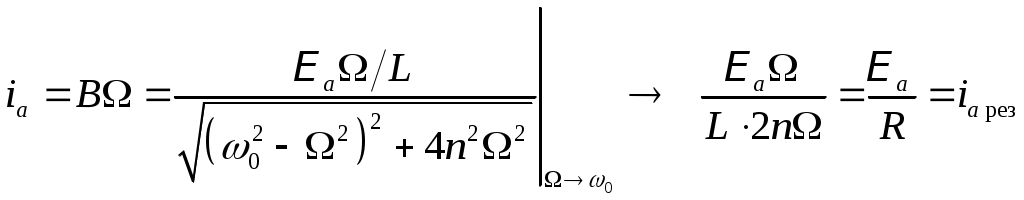. (21.17)

Р ассмотренная ситуация соответствует резонансу напряжений в цепи переменного тока, а формула амплитудного тока (21.17) в общем виде соответствует закону Ома для цепи переменного тока. Так как , n = R / 2L, то

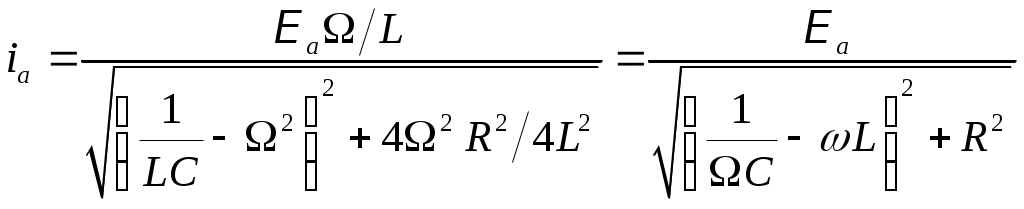. (21.18)

На рис.154 показаны амплитудные резонансные кривые – графики зависимости амплитудного тока i_a от частоты  внешней ЭДС. Чем больше добротность контура Q = R, тем уже его резонансная кривая, тем выше его избирательность (селективность). Поэтому с увеличением добротности Q ширина вынуждающих частот (  ₀), при которых в контуре раскачиваются значительные токи, становится уже. Этот интервал частот, близких к ₀, называется полосой пропускания контура. Сюда входят частоты от ₁ до ₂, где ₁ и ₂ – частоты, при которых энергия колебания в 2 раза меньше энергии колебаний в резонансе. Можно показать, что  = 2n.

Действительно, энергия амплитудного тока в резонансе

. (21.19)

Если при некоторой частоте , энергия амплитудного тока в 2 раза меньше, то есть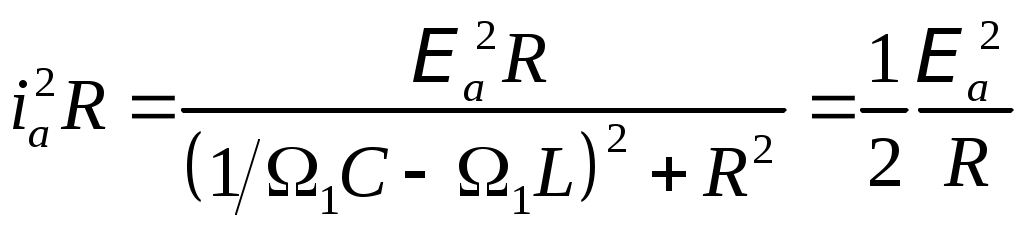

, (21.20)

то отсюда найдётся ₁. Чтобы равенство (21.20) выполнялось, должно быть

, или . (21.21)

Решение этого квадратного уравнения: 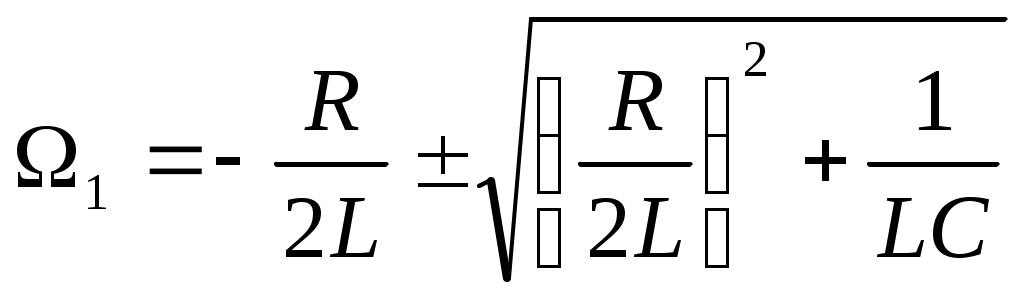. (21.22)

По условию, принятому вначале, затухание очень слабое, (R2L)² << (1LC). Поэтому первым слагаемым под корнем можно пренебречь. ₁ =  n  ₀. (21.23)

Значение ₁ =  n  ₀ < 0 и не имеет физического смысла. Остаётся ₁ = ₀  n. (21.24)

Полуширина полосы пропускания , (21.25)

а ширина полосы пропускания в 2 раза больше . (21.26)

6. Индуктивность тороидального соленоида. Пусть на тороидальный сердечник с магнитной проницаемостью μ и длиной осевой линии l намотано N витков изолированного провода (рис.118). Если по виткам катушки идёт ток I, то, как показано в примере 13.2 на с.__, магнитная индукция поля в сердечнике равна . (1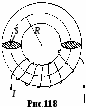6.9)

М агнитный поток, пронизывающий каждый виток, равен BS, а поток, через все витки, в N раз больше, . (16.10)

Здесь S – площадь сечения сердечника.

Этот же магнитный поток можно определить ещё как магнитный поток произвольного контура с индуктивностью L, то есть Ф = LI. Отсюда ;  . (16.11)

Индуктивность катушки растёт пропорционально квадрату числа витков N² и проницаемости сердечника .

Эта формула применима так же для вычисления индуктивности L отрезка длинной l бесконечно длинного соленоида сечением S, содержащего на этом отрезке N витков.

7. Энергия магнитного поля. Если ток в контуре изменяется на величину di, то магнитный поток поля этого тока изменяется на величину dФ = Ldi. Но это изменение потока dФ сопряжено с работой тока dA = idФ.

Если ток увеличивается, то работа тока идёт на увеличение энергии контура с током, так что dA = dW. Отсюда dW = dA = idФ = Lidi. При увеличении тока от 0 до I энергия контура найдётся интегрированием: . (16.12)

Итак, контур индуктивностью L, по которому протекает ток I, имеет запас энергии LI²2. Это энергия магнитного поля, придающая электрическую инертность контуру. При замыкании цепи требуется время на накапливание этой энергии, а при размыкании – время на её расходование. Мерой электрической инертности контура является его индуктивность.

8. Плотность энергии магнитного поля. Для её вычисления рассмотрим секцию бесконечно длинного соленоида длинной l. Полагаем, что на этом отрезке l намотано N витков, магнитная проницаемость сердечника соленоида , его сечение S (рис.119).

Поскольку соленоид бесконечно длинный, то всё магнитное поле, создаваемое этим соленоидом, находится внутри его. Магнитное поле, создаваемое током I, идущим по N виткам на отрезке длинной l, полностью заключено внутри объёма V = l S этого отрезка.

Э 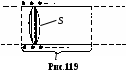нергия магнитного поля, заключённого в этом объёме V = l S, равна

. (16.13)

Разделив на объём Sl, получаем плотность энергии магнитного поля в соленоиде . (16.14)

Комбинацию параметров в скобках NIlможно выразить из формулы (13.10), определяющей индукцию магнитного поля в бесконечно длинном соленоиде. Подставив в (16.14), получаем: 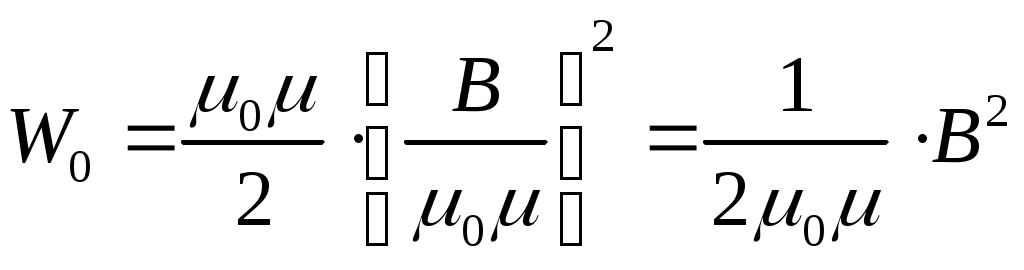. (16.15)

Если в пространстве существуют одновременно электрическое и магнитное поля, то объёмная плотность энергии электромагнитного поля в целом равна сумме энергий электрического (7.22) и магнитного (16.15) поля: . (16.16)

§17. Поле в магнетиках. Диамагнетизм

1. Магнетики. Магнитная проницаемость. Магнетиком называют любое вещество в магнитном поле. Сила взаимодействия между элементарными токами dF, определяемая законом Ампера (12.6), зависит от того, в каком веществе находится взаимодействующие токи. Её силу можно представить так: dF = mdF₀. (17.1)

где dF₀  сила взаимодействия между этими токами в вакууме. Некоторые вещества уменьшают силу взаимодействия токов по сравнению с вакуумом, другие – увеличивают.

Безразмерное число μ, показывающее во сколько раз сила взаимодействия между токами в веществе больше силы взаимодействия в вакууме, называют магнитной проницаемостью вещества.

Магнитная проницаемость μ – всегда положительное число, больше или меньше 1. Она входит в формулы законов Ампера, Био-Савара-Лапласа, электромагнитной индукции и в их многочисленные следствия.

2. Вектор намагниченности. Магнитная восприимчивость. Магнитные свойства тел обусловлены движением электрических зарядов в атомах и молекулах. Любой движущийся в оболочке атома электрон в магнитном отношении эквивалентен элементарному контуру с током, имеющему определённый магнитный момент, называемый орбитальным.

Кроме того, каждый