Лекция 4. Лекция оценка птг как территориальной единицы целевого освоения
 Скачать 136 Kb. Скачать 136 Kb.
|
|
ЛЕКЦИЯ 4. Оценка ПТГ как территориальной единицы целевого освоения Оценка ПТГ как территориальной единицы целевого освоения геосреды предполагает учет параметров техногенного образования и ресурсных возможностей регионального кластера. Из широкого разнообразия параметров оценки состояния ПТГ, необходимо выбрать наиболее показательные. С учетом бинарного подхода к ПТГ, в качестве основных параметров оценки предложены наборы структурно-геометрических, хронологических и геоэкологических характеристик, объединенных в группы. Данные группы оценивают особенности ПТГ в границах территории регионального промышленного кластера. Характеристики ПТГ, как территориальной единицы геосреды, представлены в таблице 4.1. Таблица 4.1. Характеристики оценки ПТГ, как территориальной единицы
Структурно-геометрическая группа показателей необходима для предварительной оценки линейных и объемных размеров базовых составляющих и, в конечном итоге, определения потребных количеств рекультивационных материалов. Важным показателем выступает емкость ПТГ (ЕПТГ), определяющая вклад техногенного образования в нарушение геосреды. Ее физический смысл заключается в оценке потенциальной ассимиляционной способности геосреды под влиянием техногенного образования Хронологическая группа показателей необходима для косвенной оценки стадий жизненного цикла, таких как продолжительность строительно-хозяйственной деятельности, восстановительных работ, а также экспозиции между ними или перерыва, вызванного сменой собственника, изменением законодательной базы в области восстановления земель и др. Геоэкологическая группа показателей позволяет оценить степень и характер загрязненности базовых составляющих и входящих в них элементов: почв, грунтов зоны аэрации, строительных конструкций, техногенных грунтов, отходов и линз аварийных проливов токсикантов на рельеф. Также геоэкологическая группа оценивает уровень гидрогеологической обстановки и защищенность подземных вод от загрязнения. Представленные выше группы оценивают состояние ПТГ в дискретном временном интервале исследований. Для отнесения данного интервала к выделенной стадии жизненного цикла ПТГ необходим комплексный единовременный учет максимально возможного количества характеристик базовых составляющих. Учитывая, что система оценки ПТГ является многопараметрической, а сами характеристики – разнородными величинами для определения стадии жизненного цикла целесообразно применять метод обработки многомерных данных. Метод обработки многомерных данных как инструмент оценки жизненного цикла Метод главных компонент (МГК) – это один из способов сжатия данных, который позволяет представить полезную информацию в более компактном виде, удобном для визуализации и интерпретации. Основной целью метода главных компонент является замена исходного описания образцов на новую форму, представленную в пространстве главных компонент. Это обеспечивает выделение в наборе экспериментальных данных основного сигнала и ликвидирует данные, являющиеся стохастической ошибкой. Следовательно, МГК одновременно решает две важные задачи: перевод экспериментальных данных в более подходящую систему координат (начало которой лежит в центре области данных) и, кроме того, уменьшение размерности (использование только нескольких первых главных компонент, которые отражают структуру данных). МГК применяют к данным, записанным в виде матрицы Х - прямоугольной таблицы чисел размерностью I строк и J столбцов (рисунок 2.7). Строки такой матрицы называются образцами (от 1 до I) , а столбцы - переменными (от 1 до J). 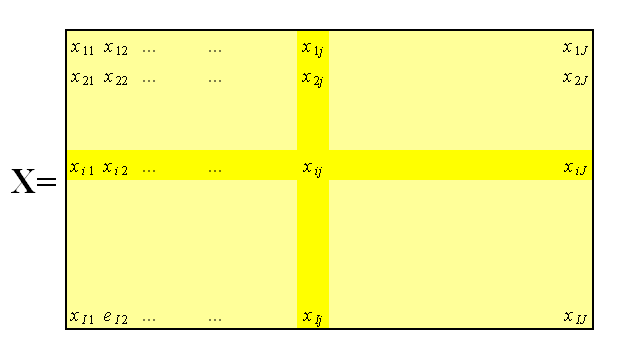 Рисунок 2.7 - Матрица исходных данных Х Для существенного понижения размерности данных исходная матрица Х заменяется двумя новыми матрицами Т и Р, размерность которых, А, меньше, чем число столбцов J у исходной матрицы Х (рисунок 2.8). Число строк I при этом сохраняется. Правильно выбранная размерность А позволяет сохранить в матрице Т полезную информацию, которую содержалась в исходной матрице Х, при этом матрица T меньше, и, следовательно, проще, чем X. 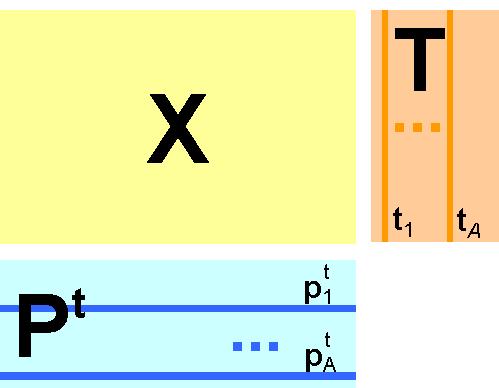 Рисунок 2.8 - Декомпозиция матрицы Х В методе главных компонент используются новые, формальные переменные ta (a=1,…A), являющиеся линейной комбинацией исходных переменных xj (j=1,…J).
С помощью этих новых переменных матрица X разлагается в произведение двух матриц T и P (рисунок 2.9): Матрица T называется матрицей счетов с размерностью (I×A). Матрица P называется матрицей нагрузок с размерностью (J×A) (рисунок 2.10). E – матрица остатков, размерностью (I×J). Pt - транспонированная матрица нагрузок Р. 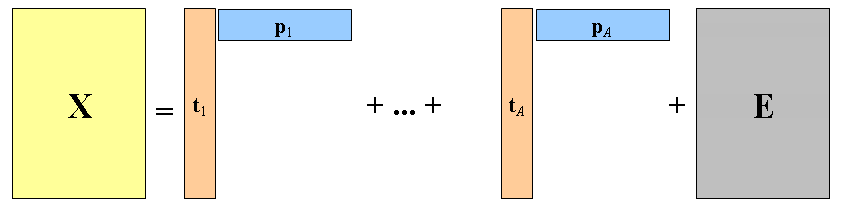 Рисунок 2.9 - Разложение матрицы Х 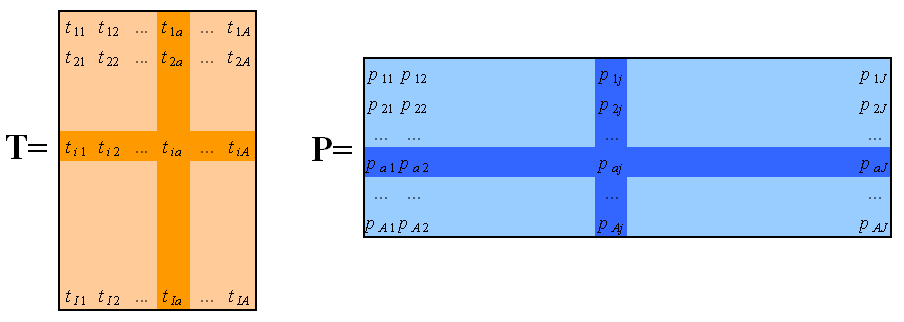 Рисунок 2.10 - Матрица счетов и матрица нагрузок Новые переменные ta называются главными компонентами. Число столбцов – ta в матрице T, и pa в матрице P, равно A, которое называется числом главных компонент. Эта величина заведомо меньше числа переменных J и числа образцов I. МГК можно интерпретировать как проекцию исходных данных X на пространство меньшей размерности A. Набор ti из I векторов-строк (размерностью A), составляющих матрицу T, представляет проекции исходных образцов (J –мерных векторов x1,…,xI) на новое подпространство (А-мерное). Строки t1,…,tI матрицы T – это координаты образцов в новой системе координат. Матрица нагрузок P – это матрица перехода из исходного пространства переменных x1, …xJ (J-мерного) в пространство главных компонент (A-мерное). Каждая строка матрицы P состоит из коэффициентов, связывающих переменные t и x (*). Например, a-я строка – это проекция всех переменных x1, …xJ на a-ю ось главных компонент. Каждый столбец P – это проекция соответствующей переменной xj на новую систему координат. Набор ta из A векторов-столбцов матрицы T представляет проекцию всех образцов на a-ую ось главных компонент. В результате преобразования появляется возможность представить сложные данные в более простом виде, так чтобы исследователь смог «увидеть» результаты экспериментов в простой графической интерпретации. На графике счетов (рисунок 2.11) каждый образец изображается в координатах (ti, tj). Чаще всего используют первые две ГК – (t1, t2). Близость двух точек-образцов на таком графике означает их схожесть, т.е. положительную корреляцию. Точки, расположенные под прямым углом, являются некоррелированными, а расположенные диаметрально противоположно – имеют отрицательную корреляцию. 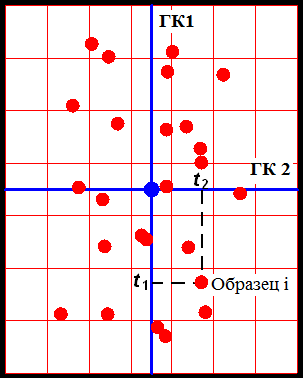 Рисунок .2.11 - График счетов График нагрузок применяется для исследования роли переменных. На нем каждая исходная переменная отображается точкой в координатах (pi, pj), например (p1, p2). Анализируя его аналогично графику счетов, можно понять, какие переменные связаны, а какие независимы. В основе пошаговых вычислений главных компонент лежит NIPALS-алгоритм, который на каждом шагу вычисляет одну компоненту. Сначала исходная матрица X преобразуется (например, центрируется) и превращается в матрицу E0, при a=0. Далее применяют следующий алгоритм: 1. Выбрать начальный вектор t; 2. pt = tt Ea / ttt; 3. p = p / (ptp)½; 4. t = Ea p / ptp; 5. Проверить сходимость, если нет, то возвратиться к пункту 2. После вычисления очередной (a-ой) компоненты, полагается ta=t и pa=p. Для получения следующей компоненты вычисляются остатки Ea+1 = Ea – tpt , а затем применяется к ним тот же алгоритм, с заменой индекса a на a+1. Декомпозиция матрицы X является последовательным, итеративным процессом, который можно оборвать на любом шаге a=A. Получившаяся матрица - Х’=ТРt отличается от матрицы X. Разница между ними Е = Х - Х’ называется матрицей остатков. Перед выполнением декомпозиции, матрица X должна быть преобразована с помощью центрирования и/или нормирование. Целью такой предварительной подготовки является преобразование исходных данных в форму, наиболее удобную для анализа. Центрирование – это вычитание из исходной матрицы X матрицы M, т.е. X'=X–M. Обычно центрирование проводится по столбцам: для каждого вектора xj вычисляются среднее значение - mj: 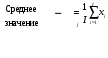 тогда M=(m11,..., mJ1), где 1 – это вектор из единиц размерности I. Второе простейшее преобразование данных, нормирование, не является обязательным. Нормирование, в отличие от центрирования, не меняет структуру данных, а просто изменяет вес различных частей данных при обработке. Чаще всего применяется нормирование по столбцам – это умножение исходной матрицы X справа на матрицу W, т.е. Матрица W – это диагональная матрица размерности J×J. Обычно диагональные элементы wjj равны обратным значениям стандартного отклонения, вычисленным для каждого столбца xj. 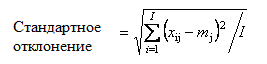 Нормирование по строкам (называемое также нормализацией) – это умножение матрицы X слева на диагональную матрицу W, т.е. При этом размерность W равна I×I, а ее элементы wii – это обратные значения стандартных отклонений строк xit. Число главных компонент, A, выбирается с использованием различных критериев. Одним из них является величина объясненной дисперсии, которая вычисляется по матрице остатков E. 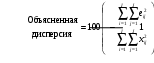 , , где e2ij - квадрат расстояния между исходным вектором xi и его проекцией на пространство PC Величина объясненной дисперсии обычно изображается на графике в зависимости от числа главных компонент; тогда ее резкое изменение указывает на нужное значение числа главных компонент A. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
