Лекция 9 Планирование эксперимента. Лекция Планирование эксперимента
 Скачать 183.51 Kb. Скачать 183.51 Kb.
|
1 2 Экспериментально-статистические методы в основном базируются на использовании пассивного и активного эксперимента. При пассивном эксперименте исследователь находится в роли пассивного наблюдателя. Эксперимент ведет сама природа. Экспериментатору приходится только фиксировать значения входных и выходных величин. Модели, полученные методом пассивного эксперимента, почти не удается проверить на адекватность. При активном эксперименте исследователь вмешивается в процесс эксперимента путем варьирования уровней входных величин. В рамках активного эксперимента построение модели проходит следующие этапы: 1) выбирается форма модели процесса; 2) строится план эксперимента; 3) проводится экспериментирование; 4) дается анализ результатов эксперимента. На практике экспериментатору приходится чаще планировать не один, а несколько экспериментов, выполняя и анализируя каждый и, в соответствии с результатами, изменять план эксперимента. Стратегия такого эксперимента показана на рис. 4.5. 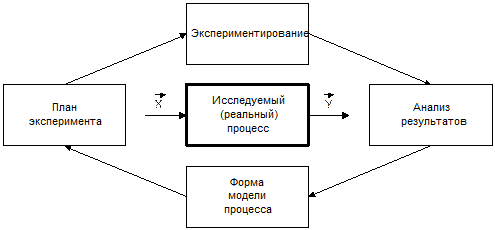 Рис. 4.5. Стратегия эксперимента Применяя системный подход к планированию машинных экспериментов, можно выделить две составляющие планирования: стратегическое и тактическое планирование. Стратегическое планированиеставит своей целью решение задачи получения необходимой информации о системе S с помощью модели Мм, реализованной на ЭВМ. По своей сути стратегическое планирование аналогично внешнему проектированию при создании системы S, только здесь в качестве объекта выступает процесс моделирования системы. При стратегическом планировании машинных экспериментов возникает ряд проблем, взаимно связанных с особенностями функционирования моделируемого объекта (системы S), с особенностями машинной реализации модели Мми обработки результатов эксперимента. В первую очередь к таким проблемам относятся: проблемы построения плана машинного эксперимента; наличие большого количества факторов; многокомпонентность функции реакции; проблема стохастической сходимости результатов машинного эксперимента; ограниченность машинных ресурсов на проведение эксперимента. Основная проблема стратегического планирования машинных экспериментов – это наличие большого количества факторов. Если факторы xi i=1, k, являются количественными, а реакция у связана с факторами некоторой функцией,то в качестве метода обработки результатов эксперимента может быть выбран регрессионный анализ. Когда при моделировании требуется полный факторный анализ, то проблема большого количества факторов может не иметь решения. Достоинством полных факторных планов является то, что они дают возможность отобразить всю поверхность реакции системы, если количество факторов невелико. Эффективность этого метода существенно зависит от природы поверхности реакции. Следующей проблемой стратегического планирования является многокомпонентность функция реакции. В имитационном эксперименте с вариантами модели системы S на этапе ее проектирования часто возникает задача, связанная с необходимостью изучения большого числа переменных реакции. Эту трудность в ряде случаев можно обойти, если разделить имитационный эксперимент на несколько имитационных экспериментов, в каждом из которых исследуется (наблюдается) только одна реакция. Проблема стохастической сходимости результатов машинного эксперимента возникает вследствие того, что целью проведения конкретного эксперимента при исследовании и проектировании системы S является получение на ЭВМ количественных характеристик процесса функционирования системы S с помощью машинной модели Мм. В качестве таких характеристик наиболее часто выступают средние значения, находящиеся путем многократных прогонов модели на ЭВМ, причем, чем больше выборка, тем больше вероятность того, что выборочные средние приближаются к истинным средним. Сходимость выборочных средних с ростом объема выборки называется стохастической сходимостью. Следовательно, необходимо большое количество экспериментов. В стратегическом планировании машинных экспериментов можно выделить следующие этапы: 1) построение структурной модели; 2) построение функциональной модели. Структурная модель выбирается исходя из того, что должно быть сделано, а функциональная — из того, что может быть сделано. Структурная модель плана эксперимента характеризуется числом факторов и числом уровней для каждого фактора. Число элементов эксперимента равно где k — число факторов эксперимента; q — число уровней i-го фактора, i=1, k. При этом под элементом понимается структурный блок эксперимента, определяемый как простейший эксперимент в случае одного фактора и одного уровня. Функциональная модель плана эксперимента определяет количество элементов структурной модели Nф, т. е. необходимое число различных информационных точек. При этом функциональная модель может быть полной и неполной. Функциональная модель называется полной, если в оценке реакции участвуют все элементы, т. е. Nф = Nс, и неполной, если число реакций меньше числа элементов, т. е. Nф Таким образом, использование при стратегическом планировании машинных экспериментов структурных и функциональных моделей плана позволяет решить вопрос о практической реализуемости модели на ЭВМ исходя из допустимых затрат ресурсов на моделирование системы S. Тактическое планированиепредставляет собой определение способа проведения каждой серии испытаний машинной модели, предусмотренных планом эксперимента, и оно связано с вопросами эффективного использования выделенных для эксперимента машинных ресурсов. Тактическое планирование машинного эксперимента связано, прежде всего, с решением следующих проблем: 1) определения начальных условий и их влияния на достижение установившегося результата при моделировании; 2) обеспечения точности и достоверности результатов моделирования; 3) уменьшения дисперсии оценок характеристик процесса функционирования моделируемых систем; 4) выбора правил автоматической остановки имитационного эксперимента с моделями систем. Первая проблема при проведении машинного эксперимента возникает вследствие искусственного характера процесса функционирования модели Мм, которая в отличие от реальной системы S работает эпизодически. Решение второй проблемы тактического планирования связано с оценкой точности и достоверности результатов моделирования (при конкретном методе реализации модели, например, методе статистического моделирования на ЭВМ) при заданном числе реализаций (объеме выборки), и с оценкой необходимого числа реализаций при заданных точности и достоверности результатов моделирования системы S. С выбором количества реализаций при обеспечении необходимой точности и достоверности результатов тесно связана проблема уменьшения дисперсии. В настоящее время существуют методы, позволяющие при заданном числе реализаций увеличить точность оценок, полученных на машинной модели Мм, и, наоборот, при заданной точности оценок сократить необходимое число реализаций при статистическом моделировании. Эти методы используют априорную информацию о структуре и поведении моделируемой системы S и называются методами уменьшения дисперсии. Простейший способ решения проблемы автоматической остановки имитационного эксперимента – задание требуемого количества реализаций N, или длины интервала моделирования Т. Однако такой подход неэффективен, так как в его основе лежат достаточно грубые предположения о распределении выходных переменных, которые на этапе планирования являются неизвестными. Другой способ – задание доверительных интервалов для выходных переменных и остановка прогона машинной модели Мм при достижении заданного доверительного интервала, что позволяет теоретически приблизить время прогона к оптимальному. Однако, введение в модель Ммправил остановки и операций вычисления доверительных интервалов увеличивает машинное время, необходимое для получения одной точки. Правила автоматической остановки могут быть включены в машинную модель следующими способами: 1) путем двухэтапного проведения прогона, когда сначала делается пробный прогон из N* реализаций, позволяющий оценить необходимое количество реализаций N (причем если N*≥N, то прогон можно закончить, в противном случае количество реализаций необходимо дополнить (набрать еще N—N* реализаций); 2) путем использования последовательного анализа для определения минимально необходимого количества реализаций N, которое рассматривается при этом как величина, зависящая от результатов N—1 предыдущих реализаций эксперимента. Таким образом, чем сложнее машинная модель Мм, тем важнее этап тактического планирования машинного эксперимента. Процесс планирования машинных экспериментов смоделью Мм носит итерационный характер, т. е. при уточнении некоторых свойств моделируемой системы S этапы стратегического и тактического планирования экспериментов могут чередоваться. Представим модели в следующем виде: где x – факторы (входные величины); b – неизвестные параметры (коэффициенты); h – реакция системы (выходная величина). Целью анализа экспериментальных данных является определение оценок неизвестных параметров b в некоторой заданной области факторного пространства X. Рассмотрим статистическую модель (рис. 4.6).  Рис. 4.6. Модель системы В реальных условиях, из-за наличия помехи e, вместо истинного значения выходной величины h экспериментатор измеряет величину Y=Y(x,b). Чтобы правильно и точно оценить параметры модели, оценки должны быть: несмещенными, состоятельными, эффективными. Оценки b являются несмещенными, если их математические ожидания равны истинным значениям параметров: M[b]=b. Это значит, что в процессе вычисления параметров модели не должны возникать статистические ошибки. Оценка называется состоятельной, если при увеличении числа наблюдений n до бесконечности она сходится по вероятности к истинному значению параметра: Достаточное условие для этого Оценки будут эффективными, если они позволяют получить максимальную информацию из наблюдений. Часто бывает, что из исследуемого параметра можно найти несколько состоятельных оценок. Чтобы выбрать одну из них сравнивают дисперсии всех оценок и по минимуму дисперсии получают оценку, которая и будет эффективной где D[b] - дисперсия оценки b, Существует несколько различных методов оценивания параметров: - максимального правдоподобия; - моментов; - оценивание по Байесу; - наименьших квадратов. Метод максимального правдоподобия базируется на использовании априорной информации, полученной из эксперимента. При этом методе получают выборку значений случайной величины X(x1,x2,...,xn) и рассматривают оцениваемые параметры b как случайные величины с некоторым законом распределения вероятности. Затем это распределение перестраивается таким образом, чтобы получить апостериорное распределение вероятности, плотность которого несет информацию о возможных значениях b на основе экспериментальных данных X. Этот метод приводит к эффективным и состоятельным оценкам, однако оценки могут быть смещенными. Метод моментов является одним из наиболее старых методов. При его использовании вычисляются первые n моментов случайной величины, которые затем приравниваются выборочным моментам. После этого находят n значений оцениваемых параметров b. Оценивание по Байесу, как и метод максимального правдоподобия, основывается на использовании априорной информации. Определяется плотность распределения вероятностей случайных величин x, и на основе апостериорной информации принимается решение. Метод наименьших квадратов (МНК) основывается на суммировании квадратов ошибок. Этот метод является самым распространенным методом при оценивании параметров модели. При выборе методов обработки существенную роль играют три особенности машинного эксперимента с моделью системы S. 1. Возможность получать большие выборки позволяет количественно оценить характеристики процесса функционирования системы, но имеется серьезная проблема хранения промежуточных результатов моделирования. Эту проблему можно решить, используя рекуррентные алгоритмы обработки, когда оценки вычисляют по ходу моделирования. 2. Сложность исследуемой системы часто приводит к тому, что априорное суждение о характеристиках процесса функционирования системы, например о типе ожидаемого распределения выходных переменных, является невозможным. Поэтому при моделировании систем широко используются непараметрические оценки и оценки моментов распределения. 3. Блочность конструкции машинной модели Мм и раздельное исследование блоков связаны с программной имитацией входных переменных одной частичной модели по оценкам выходных переменных другой частичной модели. Если ЭВМ не позволяет воспользоваться переменными, записанными на внешние носители, то следует представить эти переменные в форме, удобной для построения алгоритма их имитации. При исследовании сложных систем и большом числе реализаций N в результате моделирования получается значительный объем информации о состояниях процесса функционирования системы. Поэтому фиксацию и обработку результатов моделирования необходимо так организовать, чтобы оценки для искомых характеристик формировались постепенно по ходу моделирования, т. е. без специального запоминания всей информации о состояниях системы S. Если при моделировании системы S учитываются случайные факторы, то и среди результатов моделирования присутствуют случайные величины. В этом случае в качестве оценок для искомых характеристик рассчитывают средние значения, дисперсии, корреляционные моменты и т. д. Для оценки вероятных значений случайной величины, т. е. закона распределения, область возможных значений случайной величины h разбивается на п интервалов. Затем накапливается количество попаданий случайной величины в эти интервалы тk, к=1, п. Оценкой вероятности попадания случайной величины в интервал с номером k служит частота попадания в него – mk/N. Для оценки среднего значения случайной величины 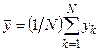 . .При этом ввиду несмещенности и состоятельности оценки В качестве оценки дисперсии случайной величины h можно использовать выражение 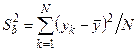 . .Более рационально оценивать дисперсию с помощью следующим образом: 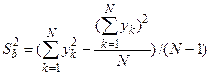 . .При обработке результатов машинного эксперимента с наиболее часто возникают следующие задачи: определение эмпирического закона распределения случайной величины, проверка однородности распределений, сравнение средних значений и дисперсий переменных, полученных в результате моделирования, и т. д. Эти задачи с точки зрения математической статистики являются типовыми задачами по проверке статистических гипотез. Задача определения эмпирического закона распределения случайной величины наиболее общая из перечисленных, но для правильного решения она требует большого числа реализаций N. В этом случае по результатам машинного эксперимента находят выборочный закон распределения Fэ(y) (либо плотность распределения fэ(y)) и выдвигают нулевую гипотезу Н0, что полученное распределение согласуется с каким-либо теоретическим распределением. Выбор вида теоретического распределения F(y) (или f(y)) проводится по графику зависимости выборочного закона распределения. Далее эту гипотезу Н0 проверяют на состоятельность с помощью статистических критериев согласия: Колмогорова, Пирсона, Смирнова и т. д.. При этом необходимую статистическую обработку результатов по возможности ведут в процессе моделирования системы. Если вероятность расхождения теоретического и эмпирического распределений Р { UT≥ U} согласно выбранному критерию согласия не велика, то проверяемая гипотеза о виде распределения Н0 принимается. Критерий согласия Колмогорова основан на выборе в качестве меры расхождения U величины Из теоремы Колмогорова следует, что при 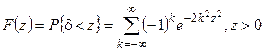 , ,где Если вычисленное на основе экспериментальных данных значение Критерий Колмогорова целесообразно применять для обработки результатов моделирования в тех случаях, когда известны все параметры теоретической функции распределения. Недостаток использования этого критерия связан с необходимостью фиксации в памяти ЭВМ всей информации. Критерий согласия Пирсона основан на определении в качестве меры расхождения экспериментального и теоретического законов распределениявеличины 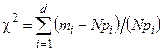 , ,где тi— количество значений случайной величины h, попавших в i-й подынтервал; pi — вероятность попадания случайной величины h в i-й подынтервал, вычисленная из теоретического распределения; d — количество подынтервалов, на которые разбивается интервал измерения в машинном эксперименте. При Из теоремы Пирсона следует, что, какова бы ни была функция распределения F(y) случайной величины h, при 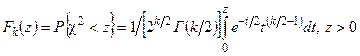 .где Г(k/2) — гамма-функция; z — значение случайной величины .где Г(k/2) — гамма-функция; z — значение случайной величины По вычисленному значению U= Хотя рассмотренные оценки искомых характеристик процесса функционирования системы S являются простейшими, они охватывают большинство случаев, встречающихся в практике обработки результатов моделирования системы. Метод наименьших квадратов Рассмотрим применение метода наименьших квадратов на примере линейной модели с одной независимой величиной. Уравнение модели с одной независимой величиной имеет вид: Оценкой уравнения (4.4) будет: Зависимость (4.4) представляет собой уравнение теоретической линии регрессии, а (4.5) – эмпирической линию регрессии (рис.4.7). Коэффициенты b0 и b1 являются оценками истинных коэффициентов b0 и b1. 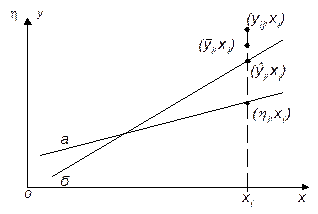 Рис. 4.7. Линия регрессии: а – теоретическая линия регрессии; б – эмпирическая линия регрессии На рис. 4.7 обозначены точки Для несмещенных оценок и тогда коэффициенты b0 и b1 могли быть определены решением системы уравнений (4.6). Однако, в реальных условиях левая часть (4.6) отличается от нуля на величину ei Величина ei называется невязкой. Она может быть вызвана ошибкой эксперимента или неправильным выбором линейной модели. Поэтому возникает задача найти такие коэффициенты уравнения регрессии, при которых невязка будет минимальной. Лучшей оценкой минимума ошибки является выражение 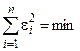 . .Это выражение приводит к методу наименьших квадратов: 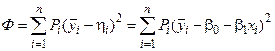 , (4.8) , (4.8)где Минимум функции Ф достигается при одновременном равенстве нулю частных производных этой функции по всем искомым коэффициентам: 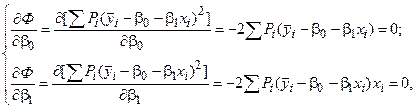 (4.9) (4.9)где После замены b0 и b1 их оценками b0 и b1 получаем систему нормальных уравнений: 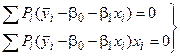 или 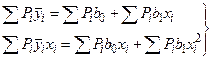 (4.10) (4.10)Решая систему нормальных уравнений относительно b0 и b1 получаем: 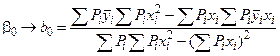 , (4.20) , (4.20)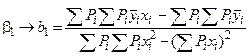 . (4.21) . (4.21)Аналогичную методику можно применить для оценки динамических характеристик. Регрессионный анализдает возможность построить модель, наилучшим образом соответствующую набору данных, полученных в ходе машинного эксперимента. Под наилучшим соответствием понимается минимизированная функция ошибки, являющаяся разностью между прогнозируемой моделью и данными эксперимента. Такой функцией ошибки при регрессионном анализе служит сумма квадратов ошибок. После нахождения коэффициентов модели возникает задача установления пригодности модели и значимости коэффициентов. С этого момента метод наименьших квадратов превращается в регрессионный анализ. Применение регрессионного анализа возможно только при выполнении следующих предположений. 1. Математическое ожидание величины 2. Значения 3. Дисперсия ошибки 4. Различные измерения величины y взаимно независимы. При выполнении этих четырех условий МНК дает несмещенные оценки b0 и b1 параметров b0 и b1 . В случае нахождения доверительной области для коэффициентов b0 и b1 должно выполняться еще одно предположение. 5. Условие распределения С помощью корреляционного анализаисследователь может установить, насколько тесна связь между двумя (или более) случайными величинами, наблюдаемыми и фиксируемыми при моделировании конкретной системы S. Корреляционный анализ результатов моделирования сводится к оценке разброса значений случайной величины h относительно среднего значения 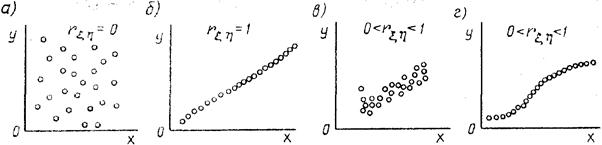 Рис. 4.9. Различные случаи корреляции переменных Для оценки точности полученного по результатам моделирования оценки коэффициента корреляции используется коэффициент w = ln [(1+ rxh)/(1-rxh)]/2, причем w приближенно подчиняется гауссовскому распределению со следующими средним значением и дисперсией: Наличие статистически значимой корреляционной зависимости между переменными модели можно сделать проверкой гипотезы Н0 о том, что rxh=0. Если гипотеза Н0 при анализе отвергается, то корреляционную зависимость признают статистически значимой. Очевидно, что выборочное распределение введенного в рассмотрение коэффициента w при rxh= 0 является гауссовским с нулевым средним mw= 0 идисперсией При анализе результатов моделирования важно отметить то обстоятельство, что даже если удалось установить тесную зависимость между двумя переменными, то отсюда еще не следует их причинно-следственная взаимообусловленность. Возможна ситуация, когда случайные x и h стохастически зависимы, хотя причинно они являются для системы S независимыми. Таким образом, корреляционный анализ устанавливает связь между исследуемыми случайными переменными машинной модели и оценивает тесноту этой связи. Однако в дополнение к этому желательно располагать моделью этой зависимости, полученной после обработки результатов моделирования. При обработке и анализе результатов моделирования часто возникает задача сравнения средних выборок. Если в результате такой проверки окажется, что математическое ожидание совокупностей случайных переменных {у{1)}, {у{2)}, …, {у{n)} отличается незначительно, то статистический материал, полученный в результате моделирования, можно считать однородным (в случае равенства двух первых моментов). Это дает возможность объединить все совокупности в одну и позволяет существенно увеличить информацию о свойствах исследуемой модели Мм, а следовательно, и системы S. Так как попарное использование критериев Смирнова и Стьюдента в этом случае затруднено, в связи с наличием большого числа выборок, то для этой цели используется дисперсионный анализ. дисперсионный анализ позволяет вместо проверки гипотезы о равенстве средних значений выборок проводить проверку гипотезы о тождественности выборочной и генеральной дисперсий. Возможны и другие подходы к анализу и интерпретации результатов моделирования, но при этом необходимо помнить, что их эффективность существенно зависит от вида и свойств конкретной моделируемой системы S. Вопросы для Самопроверки 1 Дайте определение эксперимента. 2 Какие вопросы решает планирование эксперимента? 3 Перечислите виды экспериментов по способу и условиям про- ведения, форме представления полученных результатов. 4 Дайте определение математической модели объекта исследования. 5 Что называют факторами, областью определения факторов? 6 Что называют функцией отклика и поверхностью отклика? 7 Какие виды математических моделей используются при про- ведении экспериментальных исследований? 8 Перечислите этапы проведения экспериментальных исследований. 9 Перечислите основные задачи эксперимента. 10 Дайте определение параметра оптимизации. 11 Перечислите требования, предъявляемые к параметру оптимизации. 12 Что называют обобщенным параметром оптимизации? 13 В каких случаях применяют шкалу желательности? 14 Изобразите кривую желательности. Возможно ли применение кривой для определения обобщенного параметра оптимизации? 15 Требования, предъявляемые к факторам. 16 Что называют уровнями факторов и интервалом варьирования факторов? 17 Какие ограничения необходимо учитывать при выборе интервала варьирования? 18 Как зависит количество опытов в эксперименте от числа уровней факторов? 19 Дайте определение факторного пространства. 1 2 |
