Лекции. Лекция Уравнения гиперболического типа. Колебания струны df. Струна
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Лекция 5. Уравнение распространения тепла в стержне Допустим, имеется однородный стержень длины 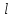 . Предположим, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. Нас интересует процесс распространения тепла в таком стержне. . Предположим, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. Нас интересует процесс распространения тепла в таком стержне.Ось 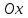 расположим так, что один конец стержня совпадает с точкой расположим так, что один конец стержня совпадает с точкой 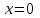 , а другой - с точкой , а другой - с точкой 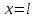 . . Пусть 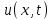 - температура в сечении стержня с абсциссой - температура в сечении стержня с абсциссой 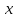 в момент времени в момент времени 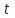 . Опытным путём установлено, что скорость распространения тепла, т.е. количество тепла, протекающего через сечение с абсциссой . Опытным путём установлено, что скорость распространения тепла, т.е. количество тепла, протекающего через сечение с абсциссой 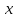 за единицу времени, определяется формулой за единицу времени, определяется формулой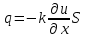 , ,где 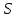 - площадь сечения стержня, - площадь сечения стержня, 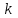 - коэффициент теплопроводности. - коэффициент теплопроводности.Рассмотрим элемент стержня, заключенный между сечениями с абсциссами 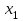 и и 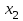 ( (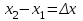 ). Количество тепла, прошедшего через сечение с абсциссой ). Количество тепла, прошедшего через сечение с абсциссой 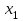 за время за время 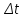 , будет равно , будет равно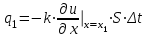 , ,а для сечения с абсциссой 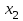 : :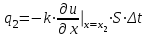 . .Приток тепла 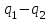 в выделенный элемент за время в выделенный элемент за время 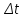 будет равен: будет равен: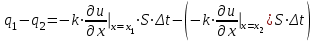 = =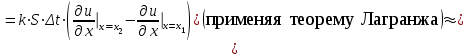 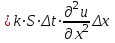 . (*) . (*)Этот приток тепла за время 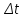 затратился на повышение температуры элемента стержня на величину затратился на повышение температуры элемента стержня на величину 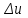 : :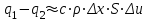 или 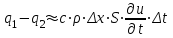 , (**) , (**)где 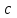 - теплоёмкость материала стержня, - теплоёмкость материала стержня, 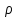 - плотность материала стержня - плотность материала стержня ( 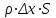 - масса выделенного элемента стержня). - масса выделенного элемента стержня).Приравняв выражения (*) и (**) одного и того же количества тепла 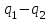 , получаем , получаем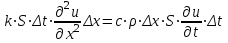 или 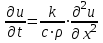 . .Далее обозначив 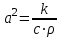 , окончательно получаем: , окончательно получаем: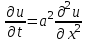 . .Это и есть уравнение распространения тепла в однородном стержне (одномерное уравнение теплопроводности). ▲ Чтобы решение уравнения теплопроводности было определено, функция 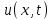 должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Краевые условия могут быть различными. Для первой краевой задачи краевые условия для должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Краевые условия могут быть различными. Для первой краевой задачи краевые условия для 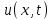 следующие: следующие: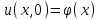 , (а) , (а)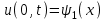 , (б) , (б)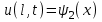 . (в) . (в)Условие (а) – начальное условие. Оно соответствует тому, что при 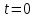 в различных сечениях стержня задана температура, равная в различных сечениях стержня задана температура, равная 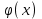 . .Условия (б), (в) – граничные условия. Они соответствуют тому, что на концах стержня при 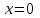 и при и при 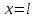 поддерживается температура, равная поддерживается температура, равная  и и 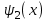 соответственно. соответственно.Доказано, что уравнение теплопроводности имеет единственное решение в области 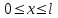 , , 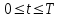 , удовлетворяющее условиям (а), (б), (в). , удовлетворяющее условиям (а), (б), (в).Распространение тепла в неограниченном стержне (Задача Коши) Задача: Определить температуру однородного бесконечного стержня в любой момент времени 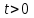 по известной температуре по известной температуре 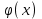 в различных сечениях в момент времени в различных сечениях в момент времени 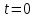 . Считать, что боковая поверхность теплоизолирована, так что тепло из стержня через неё не уходит. . Считать, что боковая поверхность теплоизолирована, так что тепло из стержня через неё не уходит.Пусть стержень совпадает с осью 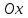 . Тогда математически задача формулируется следующим образом. Найти решение уравнения . Тогда математически задача формулируется следующим образом. Найти решение уравнения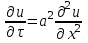 (1) (1)в области 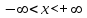 , , 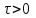 , удовлетворяющее начальному условию , удовлетворяющее начальному условию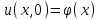 . (2) . (2)Эта задача также решается методом Фурье. Прежде чем решать поставленную задачу (1),(2), проведём вспомогательную замену переменной 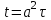 . .Тогда 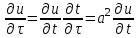 , ,и, следовательно, уравнение (1) записывается в виде 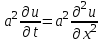 или 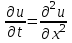 . .Начальные условия (2) не меняются, т.к. при 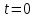 переменная переменная 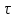 также равна нулю. также равна нулю.Таким образом, решаем следующую задачу. Найти функцию 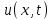 такую, что такую, что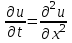 , (1) , (1)удовлетворяющую условию 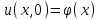 . (2) . (2)Применим метод Фурье. Решение будем искать в виде 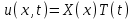 . (3) . (3)Тогда из (1): 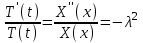 . (4) . (4)Каждое из этих соотношений не может зависеть ни от 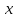 , ни от , ни от 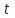 , и потому их приравниваем постоянной , и потому их приравниваем постоянной 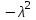 (т.к. по смыслу задачи не может неограниченно возрастать). Из (4) получаем два обыкновенных однородных дифференциальных уравнения первого и второго порядка с постоянными коэффициентами (т.к. по смыслу задачи не может неограниченно возрастать). Из (4) получаем два обыкновенных однородных дифференциальных уравнения первого и второго порядка с постоянными коэффициентами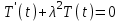 , (5) , (5)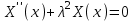 . (6) . (6)Решая их, находим 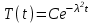 , , 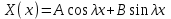 . . Подставляя эти решения в (3), получаем 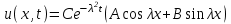 , , 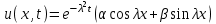 , (7) , (7)где 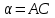 , , 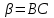 . .Путём подстановки (7) в (1) легко проверить, что (7) представляет собой частные решения уравнения (1) при любом 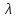 . Общее же решение уравнения (1) будет равно сумме всех частных решений (7). Однако . Общее же решение уравнения (1) будет равно сумме всех частных решений (7). Однако 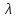 произвольно и может принять любое значение в интервале произвольно и может принять любое значение в интервале 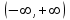 , поэтому сумму частных решений следует заменить интегралом по параметру , поэтому сумму частных решений следует заменить интегралом по параметру 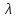 , т.е. общее решение уравнения (1) представляется в виде , т.е. общее решение уравнения (1) представляется в виде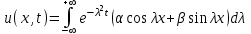 . (8) . (8)Выберем 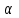 и и 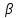 так, чтобы (8) удовлетворяло условию (2). Для этого в (8) положим так, чтобы (8) удовлетворяло условию (2). Для этого в (8) положим 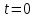 и использовав (2), получаем и использовав (2), получаем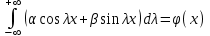 . (9) . (9)В свою очередь функция 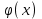 может быть представлена интегралом Фурье может быть представлена интегралом Фурье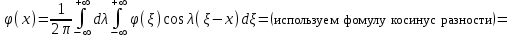 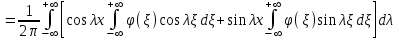 . (10) . (10)Сравнивая (9) и (10), получим 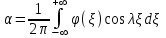 , , 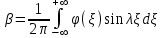 . (11) . (11)Подставляя (11) в (8), получим 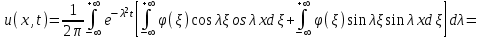 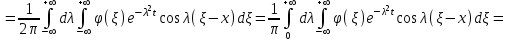 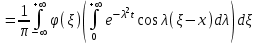 . (12) . (12)Это и есть решение поставленной задачи. Внутренний интеграл (без доказательства) можно заменить на 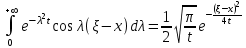 . .Подставив это выражение в (12), получим 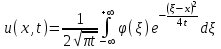 . .И, возвращаясь к старым переменным ( 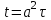 ), окончательно получаем ), окончательно получаем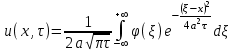 . .Эта формула, называемая интегралом Пуассона, представляет решение поставленной задачи о распространении тепла в неограниченном стержне. ▲ Доказано, что функция, определяемая интегралом Пуассона, является решением задачи (1),(2), если функция 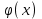 ограничена на ограничена на 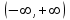 . .▲ Полезно иметь в виду формулу 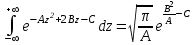 . .Лекция 6. Эллиптический тип. Уравнение Лапласа. К уравнениям эллиптического типа приводит изучение стационарных, т.е. не меняющихся во времени, процессов различной физической природы. Простейшим уравнением эллиптического типа является уравнение Лапласа. df. Уравнением Лапласа называется уравнение 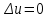 , ,где 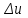 - лапласиан, который имеет вид в декартовых координатах - лапласиан, который имеет вид в декартовых координатах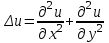 , ,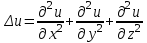 , ,и в полярных координатах 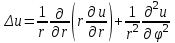 . .df. Функция, удовлетворяющая уравнению Лапласа, называется гармонической. ▲ Этому уравнению удовлетворяет стационарное распределение температуры в теле. Уравнению Лапласа удовлетворяет потенциал стационарного электрического поля, где отсутствуют заряды, и потенциал поля тяготения в области, где отсутствуют массы. Уравнение Лапласа имеет бесконечное множество решений. Какое-то конкретное решение определяется заданием некоторых дополнительных условий. Типичной для уравнения Лапласа является задача: найти функцию 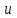 , гармоническую в области , гармоническую в области 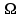 и удовлетворяющую на границе и удовлетворяющую на границе 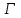 области области 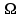 граничному условию, которое может быть одного из следующих видов: граничному условию, которое может быть одного из следующих видов: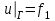 - первая краевая задача (задача Дирихле); - первая краевая задача (задача Дирихле);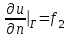 - вторая краевая задача (задача Неймана); - вторая краевая задача (задача Неймана);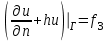 -третья краевая задача. -третья краевая задача.Здесь 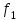 , , 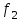 , , 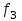 , , 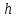 - заданные функции, - заданные функции, 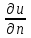 - производная в направлении внешней нормали к границе - производная в направлении внешней нормали к границе 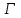 . .Задача Дирихле для круга. Решение методом Фурье. Задача ставится следующим образом: найти функцию, гармоническую внутри круга и принимающую на его границе заданные значения. Если ввести полярные координаты 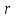 и и 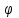 так, чтобы полюс находился в центре данного круга, радиус которого пусть так, чтобы полюс находился в центре данного круга, радиус которого пусть 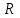 , то задача записывается в следующем виде: , то задача записывается в следующем виде: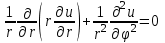 , (1) , (1)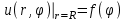 , (2) , (2)где 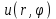 - функция, требующая определения, а - функция, требующая определения, а 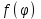 - заданная функция. - заданная функция.Будем искать решение уравнения (1) в виде 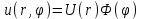 . (3) . (3)Подставим (3) в (1) и получим 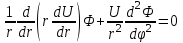 или (умножив все на 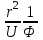 ) )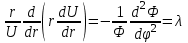 . .Последнее равенство должно выполняться для всех 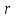 и и 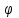 из данной области (круг: из данной области (круг: 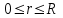 , , 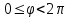 ). Это возможно лишь случае, когда обе части равенства не зависят от ). Это возможно лишь случае, когда обе части равенства не зависят от 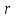 и и 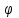 , т.е. являются одной и той же постоянной, так как левая часть его может зависеть только , т.е. являются одной и той же постоянной, так как левая часть его может зависеть только 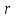 , а правая – только от , а правая – только от 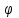 . Обозначив эту постоянную через . Обозначив эту постоянную через 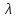 , получаем два обыкновенных дифференциальных уравнения второго порядка , получаем два обыкновенных дифференциальных уравнения второго порядка 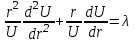 , (4) , (4)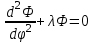 . (5) . (5)Уравнение (5) имеет общее решение 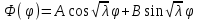 , ,где 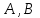 - произвольные постоянные. Что касается значений - произвольные постоянные. Что касается значений 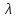 , то они не могут быть произвольными. Так как прибавление к аргументу , то они не могут быть произвольными. Так как прибавление к аргументу 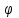 слагаемого слагаемого 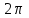 возвращает точку возвращает точку 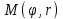 в исходное положение. Это значит, что в исходное положение. Это значит, что 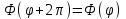 , т.е. функция , т.е. функция 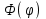 является периодической с периодом является периодической с периодом 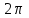 . Тогда . Тогда 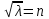 , , 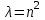 , , 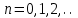 . Отрицательные значения . Отрицательные значения 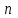 можно не принимать во внимание, поскольку знак можно не принимать во внимание, поскольку знак 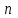 влияет только на знак влияет только на знак 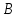 - произвольной постоянной. - произвольной постоянной.Таким образом, уравнение (5) имеет решения 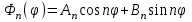 , , 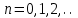 . .Уравнение (4) (уравнение Эйлера) при 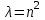 теперь принимает вид теперь принимает вид 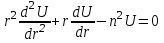 . .Решение этого уравнения находится с помощью подстановки 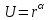 . . Так как 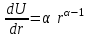 , , 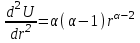 , ,то 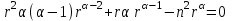 , ,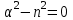 , ,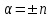 . .Если 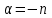 , то , то 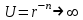 при при 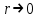 . Такая функция не может быть использована для построения решения задачи Дирихле (ищется решение непрерывное и конечное в круге). . Такая функция не может быть использована для построения решения задачи Дирихле (ищется решение непрерывное и конечное в круге).При 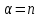 получаем получаем 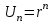 , , 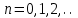 . Подставляя выражения для . Подставляя выражения для 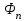 и и 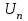 в формулу (3), записываем частные решения в формулу (3), записываем частные решения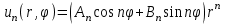 . .Решением этого уравнения (3) является также функция 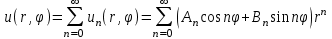 . .Коэффициенты 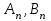 определим из граничного условия (2). При определим из граничного условия (2). При  имеем имеем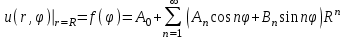 . (6) . (6)Запишем разложение функции 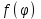 в ряд Фурье в ряд Фурье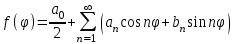 , (7) , (7)где 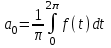 , , 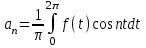 , ,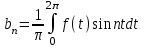 , , 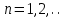 . .Сравнивая ряды (6) и (7), получаем 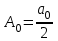 , , 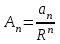 , , 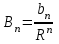 , , 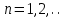 . .Таким образом, решение поставленной задачи есть 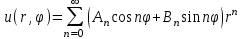 , (8) , (8)где 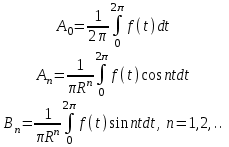 (9). (9). |
