Лекции. Лекция Уравнения гиперболического типа. Колебания струны df. Струна
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Лекция 3. Уравнения гиперболического типа. Колебания струны. df. Струна – идеально гибкая, тонкая нить, упругая лишь тогда, когда она натянута, и оказывающая сопротивление растяжению. Рассмотрим туго натянутую струну, закрепленную на концах. Выведем струну из положения равновесия (оттянув или ударив по ней), струна начнёт колебаться. Предположим, что каждая точка струны колеблется по прямой, перпендикулярной к исходному положению струны, и струна находится в одной и той же плоскости (поперечные плоские колебания). Выберем в этой плоскости декартову прямоугольную систему координат 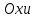 . В качестве оси . В качестве оси 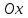 возьмём прямую, на которой находилась струна в положении равновесия, за ось возьмём прямую, на которой находилась струна в положении равновесия, за ось 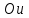 примем прямую, проходящую через левый конец струны и перпендикулярно к оси примем прямую, проходящую через левый конец струны и перпендикулярно к оси 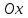 . .Отклонение струны от положения равновесия обозначим через 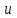 ; очевидно, ; очевидно, 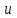 зависит от абсциссы зависит от абсциссы 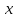 точки струны и времени точки струны и времени 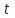 , т.е. , т.е. 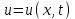 . .Чтобы составить представление о колебаниях струны, необходимо начертить ряд графиков функции 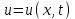 при различных значениях при различных значениях 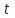 , т.е. необходимо определить функцию , т.е. необходимо определить функцию 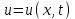 . .При фиксированном значении 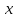 функция функция 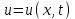 определяет закон движения точки с абсциссой определяет закон движения точки с абсциссой 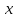 . Эта точка движется по прямой, параллельной оси . Эта точка движется по прямой, параллельной оси 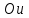 . Скорость и ускорение указанного движения выражаются формулами . Скорость и ускорение указанного движения выражаются формулами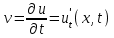 , , 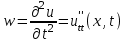 . .Будем рассматривать малые колебания струны, т.е. такие, при которых угол наклона касательной к графику функции 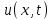 при каждом фикси-рованном значении при каждом фикси-рованном значении 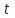 мал, то есть приближённо можно считать, что мал, то есть приближённо можно считать, что 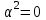 . Далее можно показать, что из этого предположения следует . Далее можно показать, что из этого предположения следует 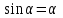 и и 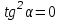 , т.е. , т.е. 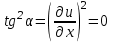 . Тогда длина дуги струны, ограниченной точками . Тогда длина дуги струны, ограниченной точками 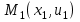 и и 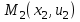 вычисляется по формуле вычисляется по формуле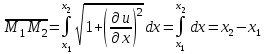 . .Последнее равенство означает, что длина любого участка струны всегда остаётся постоянной. В этих предположениях уравнение свободных колебаний струны (одномерное волновое уравнение) имеет вид 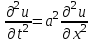 , (1) , (1)если внешние силы отсутствуют. Уравнение вынужденных колебаний имеет вид 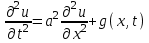 . (2) . (2)Чтобы из множества решений уравнения с частными производными второго порядка выбрать определённое решение, необходимо задать дополнительные условия. Нужно указать отклонение и скорость движения в начальный момент времени 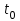 (обычно (обычно 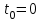 ), т.е. ), т.е.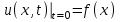 , , 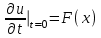 , (3) , (3)где 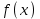 , , 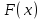 - заданные функции. - заданные функции.Нужно зафиксировать отклонения концов струны. Поскольку они закреплены, то 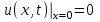 , , 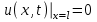 , (4) , (4)где 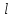 - длина струны. - длина струны.df. Условия (3) называются начальными условиями, а условия (4) называются краевыми (граничными) условиями. Таким образом, задача о свободных колебаниях струны ставится следующим образом. Найти решение 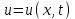 линейного однородного уравнения с частными производными второго порядка линейного однородного уравнения с частными производными второго порядка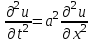 , ,удовлетворяющее начальным условиям 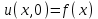 , , 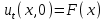 , ,и краевым условиям 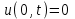 , , 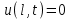 , ,причём 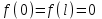 . .▲ Можно доказать, что при некоторых предположениях относительно функций 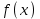 и и 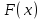 поставленная задача имеет единственное решение. поставленная задача имеет единственное решение.Задача о свободных колебаниях бесконечной струны. Метод Даламбера. Предполагается, что струна является неограниченной, поэтому задача о свободных колебаниях неограниченной струны называется задачей Коши (граничные условия не накладываются). Эта задача ставится следующим образом. Найти решение 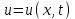 линейного однородного уравнения с частными производными второго порядка линейного однородного уравнения с частными производными второго порядка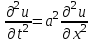 , , 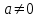 , (1) , (1)удовлетворяющее начальным условиям 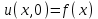 , , 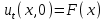 , (2) , (2)где 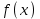 и и 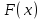 - заданные функции, определённые в бесконечном промежутке - заданные функции, определённые в бесконечном промежутке 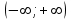 . .Перепишем (1) 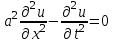 . .Определим тип уравнения. Так как 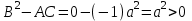 , ,то уравнение (1) гиперболического типа. Приведём уравнение (1) к каноническому виду. Для этого запишем уравнение характеристик 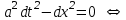 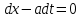 или или 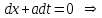 общие интегралы имеют вид 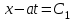 , , 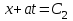 . .Введём новые переменные 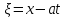 , , 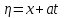 . . Пересчитаем производные, имея в виду, что 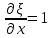 , , 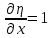 , ,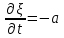 , , 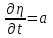 . Следовательно, . Следовательно,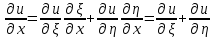 , ,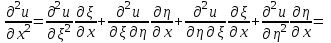 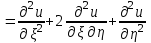 , ,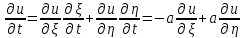 , ,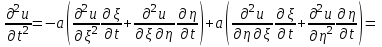 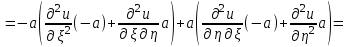 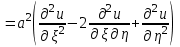 . .Подставляя эти производные в (1) 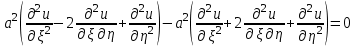 , ,получаем уравнение (1) в каноническом виде 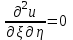 . .Проинтегрируем полученное уравнение, полагая 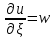 . .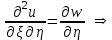 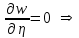 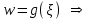 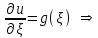 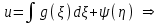 обозначая интеграл через новую функцию, получаем 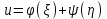 , , где 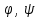 - произвольные дважды дифференцируемые функции своих аргументов. - произвольные дважды дифференцируемые функции своих аргументов.Возвращаясь к старым переменным, получаем общее решение уравнения (1) 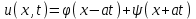 . (4) . (4)▲ С физической точки зрения общее решение (4) интересно тем, что представляет сумму двух бегущих волн произвольной формы, движущихся в противоположных направлениях со скоростью 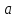 . . Теперь найдём функцию 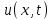 , удовлетворяющую начальным условиям (2). , удовлетворяющую начальным условиям (2).Сначала вычислим производную 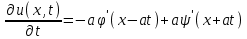 . .Условия (2) принимают следующий вид 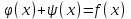 , , 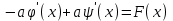 . (5) . (5)Проинтегрируем второе равенство в (5) по отрезку 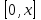 , получим , получим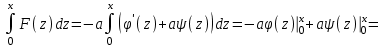 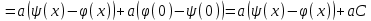 . .Откуда 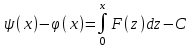 . .Теперь условия (5) можно записать в виде 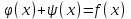 , , 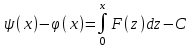 и определить из них функции 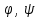 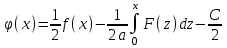 , ,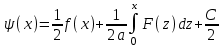 . .Подставляя в эти формулы вместо 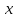 в функцию в функцию 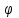 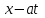 , в функцию , в функцию 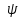 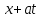 , получим , получим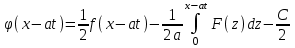 , ,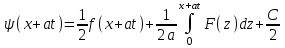 . .По формуле общего решения (4) 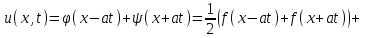 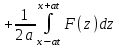 или окончательно получаем решение Даламбера 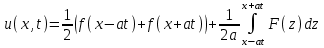 . .Лекция 4. Задача о колебаниях ограниченной струны (задача о колебаниях струны, закреплённой на концах). Метод Фурье. Задача. Найти решение 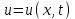 линейного однородного уравнения с частными производными второго порядка линейного однородного уравнения с частными производными второго порядка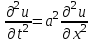 , , 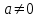 , (1) , (1)удовлетворяющее начальным условиям 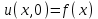 , , 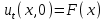 , (2) , (2)и граничным условиям 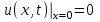 , , 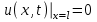 . (3) . (3)Для решения задачи (1)-(3) будем применять метод Фурье. Решение будем искать в виде 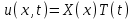 . (4) . (4)Подставим (4) в исходное уравнение (1): 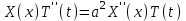 , (5) , (5)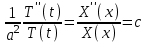 . (6) . (6)Из (6) получаем два обыкновенных однородных дифференциальных уравнения второго порядка с постоянными коэффициентами 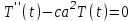 , (7) , (7)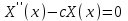 . (8) . (8)Найдём решение уравнения (8), удовлетворяющее условиям (3), которые с учётом (4)принимают вид 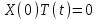 , , 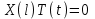 . (9) . (9)Поскольку решение должно быть нетривиальным 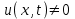 , то из (9) следует , то из (9) следует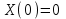 , , 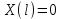 . (10) . (10)Запишем характеристическое уравнение для (8) 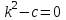 . (11) . (11)Необходимо рассмотреть три возможных случая: 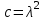 , , 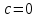 , , 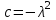 . .Случай 1. 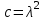 . .В этом случае характеристическое уравнение (8) имеет два различных вещественных корня 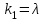 и и 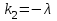 , и, следовательно, общее решение уравнение (8) записывается в виде , и, следовательно, общее решение уравнение (8) записывается в виде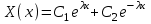 . (12) . (12)Условия (10) приводят к системе уравнений 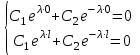 или или 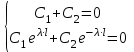 . (13) . (13)Определитель однородной системы (13) отличен от нуля 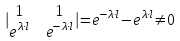 , , Следовательно, система (13) имеет единственное решение 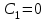 , , 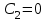 . .Таким образом, решение уравнения (8), удовлетворяющее условиям (10), есть 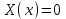 . Это решение не подходит, т.к. в этом случае функция . Это решение не подходит, т.к. в этом случае функция 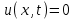 . .Случай 2. 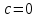 . .В этом случае характеристическое уравнение (8) имеет два одинаковых вещественных корня 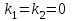 и, следовательно, общее решение уравнение (8) записывается в виде и, следовательно, общее решение уравнение (8) записывается в виде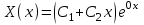 или или 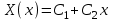 (14) (14)Условия (10) приводят к системе уравнений 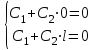 . (15) . (15)Система (14) имеет единственное решение 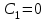 , , 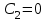 . .Таким образом, решение уравнения (8), удовлетворяющее условиям (10), и в этом случае есть 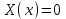 . Это решение не подходит, т.к. в этом случае функция . Это решение не подходит, т.к. в этом случае функция 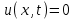 . .Случай 3. 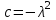 . .В этом случае характеристическое уравнение (8) имеет два комплексно-сопряженных корня 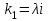 и и 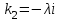 , и, следовательно, общее решение уравнение (8) записывается в виде , и, следовательно, общее решение уравнение (8) записывается в виде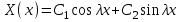 . (16) . (16)Используя условия (10), получаем систему 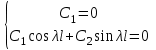 или или 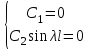 . . Так как нас интересует нетривиальное решение 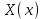 , то из второго уравнения системы имеем , то из второго уравнения системы имеем 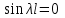 . Решение этого уравнения . Решение этого уравнения 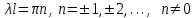 ибо ибо 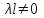 ( (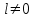 длина струны, длина струны, 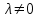 второй случай), или второй случай), или 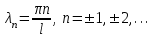 . (17) . (17)Итак, каждая из функций 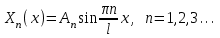 , (18) , (18)где 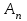 - произвольная константа (к ней отнесён знак n , т.к. синус функция нечётная), является решением уравнения (8), удовлетворяющим условиям (10). - произвольная константа (к ней отнесён знак n , т.к. синус функция нечётная), является решением уравнения (8), удовлетворяющим условиям (10).df. Постоянные 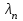 , определяемые формулой (17), называются собственными числами, а функции , определяемые формулой (17), называются собственными числами, а функции 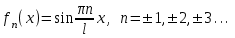 , называются собственными функциями уравнения (8). , называются собственными функциями уравнения (8).Вернёмся к уравнению (7). Так как 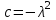 , , 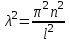 , следовательно, уравнение (7) принимает вид , следовательно, уравнение (7) принимает вид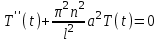 . (19) . (19)Характеристическое уравнение 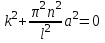 имеет мнимые корни 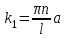 и и 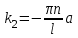 . Следовательно, общее решение уравнения (7) определяется формулой . Следовательно, общее решение уравнения (7) определяется формулой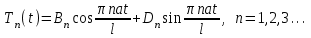 , (20) , (20)где 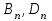 - произвольные постоянные. - произвольные постоянные.Подставляем (18) и (20) в (4). Получаем 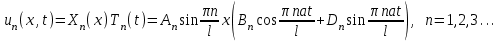 или или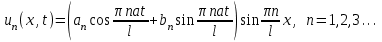 , (21) , (21)где 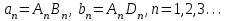 . .df. Каждая из функций (21) является решением уравнения (1), удовлетворяющим условиям (3), и называется собственной функцией этого уравнения, а колебания, определяемые ею, называются собственными колебаниями. Перейдём ко второй части метода Фурье. Составим ряд 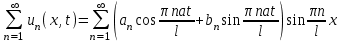 . (22) . (22)Предположим, что этот ряд равномерно сходится, его сумма является непрерывной функцией и ряд можно дважды почленно дифференцировать по xи t. Обозначим сумму этого ряда через 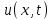 , т.е. , т.е.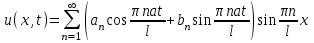 . (23) . (23)Эта функция также является решением уравнения (1), удовлетворяющая условиям (3). Коэффициенты ряда (23) выберем так, чтобы функция удовлетворяла условиям (2). Продифференцируем (23) по t, получим 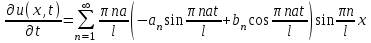 . (24) . (24)Подставляем в (23) и (24) значение t=0 и учитываем условия (2), получаем 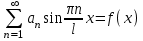 , , 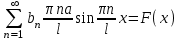 . (25) . (25)Следовательно, функции 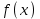 и и 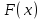 представляют собой разложения в ряд Фурье по синусам на отрезке представляют собой разложения в ряд Фурье по синусам на отрезке 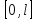 . Как известно, коэффициенты таких разложений определяются формулами . Как известно, коэффициенты таких разложений определяются формулами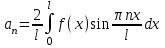 , , 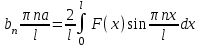 или 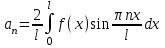 , , 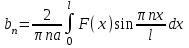 . (26) . (26)Итак, функция (23) с коэффициентами (26) дает решение рассматриваемой задачи. ▲ Из формулы (21) 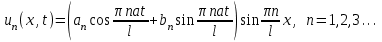 видно, что в моменты времени 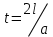 , , 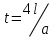 … струна возвращается в первоначальное положение. Следовательно, колебания являются незатухающими, периодическими с периодом … струна возвращается в первоначальное положение. Следовательно, колебания являются незатухающими, периодическими с периодом 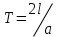 . Это происходит потому, что не учтены силы сопротивления. Если эти силы учесть, то колебания окажутся затухающими. . Это происходит потому, что не учтены силы сопротивления. Если эти силы учесть, то колебания окажутся затухающими. |
