Лекции. Лекция Уравнения гиперболического типа. Колебания струны df. Струна
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Интеграл Пуассона Формулу (8) можно преобразовать. Для этого в неё надо подставить выражения для коэффициентов (9) и произвести тригонометрические преобразования. А именно, 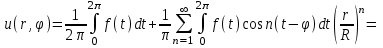 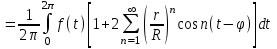 . .Принимая во внимание формулы Эйлера, получаем 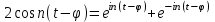 . .Следовательно, 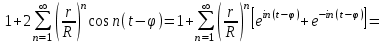 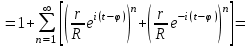 (Комплексные члены каждого ряда образуют геометрические прогрессии, знаменатели которых по модулю меньше единицы: 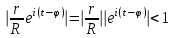 , , 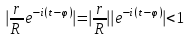 А сумма членов таких геометрических прогрессий находится по известной формуле.) 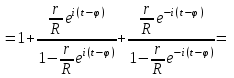 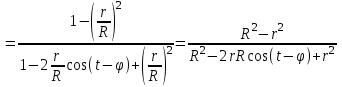 . .Таким образом, 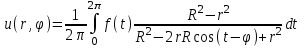 . .Эта формула называется интегралом Пуассона, и функция, определяемая этой формулой, является решением задачи Дирихле для круга. Лекция 7. Понятие о конечно-разностных методах. Для нахождения решений задач математической физики наряду с аналитическими методами (например, метод разделения переменных) используются численные методы, к которым относятся конечно-разностные методы, метод конечных элементов, метод контрольных объёмов и др. Эти методы используются для нахождения приближенных решений. Основная идея численных методов состоит в том, что исходное уравнение с заданными условиями заменяется (аппроксимируется) системой алгебраических уравнений относительно значений искомой функции в некоторых точках. Конечно-разностные аппроксимации Ряд Тейлора для функции 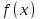 в окрестности точки в окрестности точки 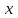 имеет вид имеет вид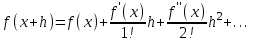 . .Если этот ряд оборвать на втором члене, то получим 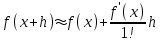 , ,откуда 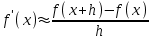 . .Выражение, стоящее в правой части, называется правой разностной производной. Она аппроксимирует первую производную 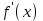 в точке в точке 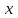 . .Если в разложении Тейлора 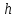 заменить на заменить на 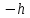 , то получится левая разностная производная , то получится левая разностная производная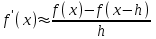 . .Если из 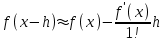 вычесть вычесть 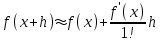 , то получится центральная разностная производная , то получится центральная разностная производная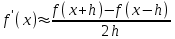 . .Если в ряде Тейлора оставить на одно слагаемое больше, то аналогично можно получить центральную разностную производную для аппроксимации 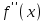 : :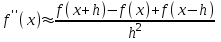 . .Теперь понятие конечно-разностной аппроксимации можно распространить на частные производные. Если исходить из разложения Тейлора 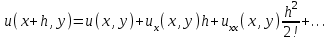 , ,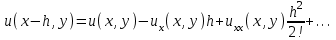 , ,можно получить следующие аппроксимации частных производных 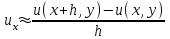 , ,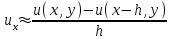 , ,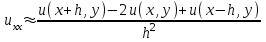 , ,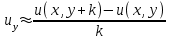 , ,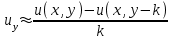 , ,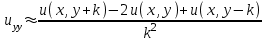 . .Решение первой краевой задачи для уравнения теплопроводности методом конечных разностей Первая краевая задача для уравнения теплопроводности ставится следующим образом. Необходимо найти функцию 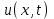 , удовлетворяющую уравнению , удовлетворяющую уравнению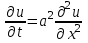 , (1) , (1)и краевым условиям 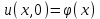 , , 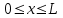 , (2) , (2)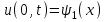 , , 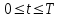 , (3) , (3)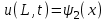 , , 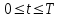 , (4) , (4)т.е. требуется найти решение 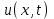 в прямоугольнике, ограниченном прямыми в прямоугольнике, ограниченном прямыми 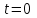 , , 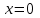 , , 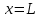 , , 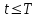 , если известны значения искомой функции на трёх сторонах этого прямоугольника: , если известны значения искомой функции на трёх сторонах этого прямоугольника: 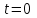 , , 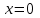 , ,  . .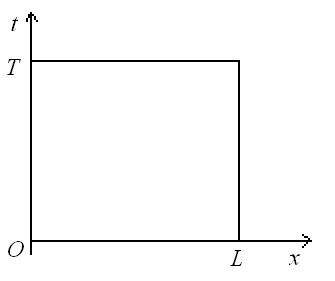 Покроём область решения задачи (прямоугольник) сеткой, образованной прямыми 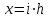 , , 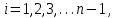 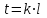 , , 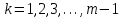 , ,где 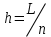 , , 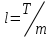 . О выборе . О выборе 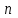 и и 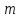 (или что тоже самое (или что тоже самое 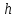 и и 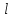 ) скажем ниже. ) скажем ниже.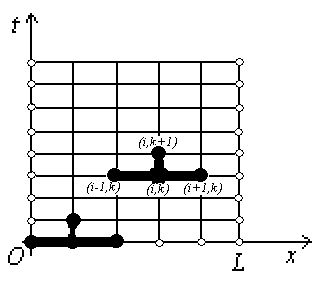 Будем искать приближённые значения решения в узлах сетки, т.е. в точках пересечения этих прямых. Введём обозначения: 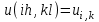 . .С помощью конечно-разностных аппроксимаций 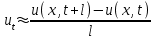 , ,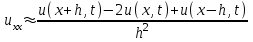 , ,запишем вместо уравнения (1) соответствующее ему уравнение в конечных разностях для точки 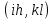 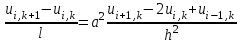 . (5) . (5)Из (5) найдём 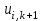 : :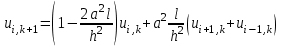 . (6) . (6)Из формулы (6) следует, что если известны три значения 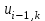 , , 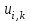 , , 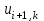 в в 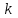 -ом ряду, то определяется значение -ом ряду, то определяется значение 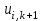 в в 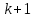 -ом ряду. Так как известны все значения функции -ом ряду. Так как известны все значения функции 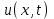 на прямой на прямой 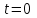 (условие (2)) и на прямых (условие (2)) и на прямых 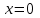 (условие (3)) и (условие (3)) и 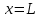 (условие (4)), то ряд за рядом определяются все значения искомого решения во всех узлах сетки. (условие (4)), то ряд за рядом определяются все значения искомого решения во всех узлах сетки.Теперь вернёмся к выбору 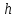 и и 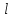 . Доказано, что по формуле (6) можно получить приближённое решение не при произвольных шагах . Доказано, что по формуле (6) можно получить приближённое решение не при произвольных шагах 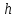 и и 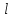 , а только в том случае, если , а только в том случае, если 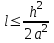 . . Формула (6) сильно упрощается, если шаг 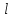 по оси по оси 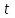 выбрать так, чтобы было выбрать так, чтобы было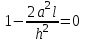 или 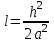 . .В этом случае формула (6) принимает удобный для вычислений вид: 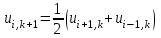 . . |
