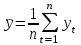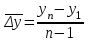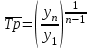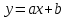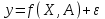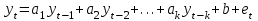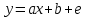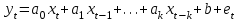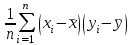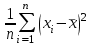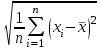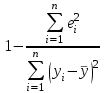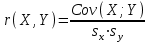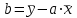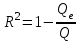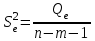ФОС. ФОС Б1.О.21 Эконометрика БИ. Льтет экономики, управления и юриспруденции Каф
 Скачать 246.92 Kb. Скачать 246.92 Kb.
|
|
Ответ: 1 _, 2 _, 3 _. 15. Для каждого элемента из левой части таблицы выберите один ответ из правой части.
Ответ: 1 _, 2 _, 3 _ 16. Для каждого элемента из левой части таблицы выберите один ответ из правой части.
Ответ: 1 _, 2 _, 3 _, 4 _, 5 _ 15. Для каждого элемента из левой части таблицы выберите один ответ из правой части.
Ответ: 1 _, 2 _, 3 _, 4 _. 18. Установить соответствие/ При исследовании связи двух показателей получены некоторые результаты. Какому из показателей соответствует каждый из результатов?
Ответ: 1 _, 2 _, 3 _ 19. Установить соответствие При исследовании связи двух показателей получены некоторые результаты. Какому из показателей соответствует каждый из результатов?
Ответ: 1 _, 2 _, 3 _ 20 Для каждого элемента из левой части таблицы выберите один ответ из правой части
Ответ: 1 _, 2 _, 3 _., 4 _. 21. Установить соответствие Для кубической параболы характерно следующее поведение приростов:
Ответ: 1 _, 2 _, 3 _ 22. Установить правильную последовательность Этапы построения эконометрической модели: Постановка проблемы (определение и формулировка конечных целей моделирования и набора участвующих в модели показателей – факторов). Оценка качества модели и ее верификация (проверка прогнозных свойств). Идентификация модели (статистическое оценивание неизвестных параметров модели и параметров распределения случайной составляющей 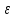 ). ).Спецификация модели – выбор формы связи переменных модели, то есть, вида функции (значения параметров модели пока неизвестны). Ответ: ___________ 23. Установить правильную последовательность При положительной асимметрии показатели центра группирования случайной величины располагаются в порядке (слева направо): 1. Среднее. 2. Мода. 3. Медиана. Ответ: ___________ 24. Установить правильную последовательность Предпосылки (предположения) к построению уравнения линейной регрессии 1. Математическое ожидание 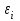 равно нулю. равно нулю.2. Значения 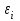 попарно не коррелированы, или, более сильно, попарно независимы между собой. Здесь i – номер в упорядоченной последовательности значений x. попарно не коррелированы, или, более сильно, попарно независимы между собой. Здесь i – номер в упорядоченной последовательности значений x. 3. Свойство гомоскедастичности: дисперсия 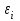 постоянна (одинакова для различных i). постоянна (одинакова для различных i).4. При заданных значениях 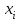 на переменную y не оказывают влияние никакие другие систематически действующие факторы, и величина на переменную y не оказывают влияние никакие другие систематически действующие факторы, и величина 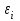 является случайной. является случайной.Ответ: ___________ 25. Установить правильную последовательность Области принятия гипотез по критерию Дарбина-Уотсона располагаются слева направо в следующее порядке: 1. H0 принимается (отсутствие автокорреляции). 2. H0 отвергается (положительная автокорреляция). 3. H0 отвергается (отрицательная автокорреляция) Ответ: ___________ 26. Установить правильную последовательность Статистический анализ уравнения множественной линейной регрессии включает: 1. Проверку предпосылок регрессионного анализа (свойств остатков: случайность, попарная независимость, гомоскедастичность, нормальность распределения). 2. Проверку общего качества уравнения регрессии; 3. Проверку статистической значимости каждого коэффициента модели; Ответ: ___________ 27. Установить правильную последовательность Построение модели временного ряда осуществляется по традиционной схеме, которая состоит из следующих этапов: 1. Графическое представление и описание поведения временного ряда. 2. Выделение и удаление закономерных составляющих временного ряда, зависящих от времени: тренда, сезонных и циклических составляющих. 3. Прогнозирование будущего развития процесса, представленного временным рядом. 4. Исследование случайной (остаточной) составляющей временного ряда (построение закона распределения). 5. Вывод суждения о наличии разного рода тенденций на основании анализа исходного процесса. Ответ: ___________ 28. Установить правильную последовательность При аналитическом выравнивании временного ряда решаются следующие задачи: 1. Выявление степени близости теоретических и фактических данных 2. Выбор метода определения параметров модели. 3. Выбор вида уравнения, отображающего тип развития. 4. Получение значений параметров модели. Ответ: ___________ 29. Установить правильную последовательность Основные этапы экстраполяционного прогнозирования экономической динамики на основе временных рядов с использованием трендовых моделей: 1. Предварительный анализ данных. 2. Формирование набора моделей-кандидатов (например, кривых роста). 3. Тестирование адекватности и точности моделей. 4. Выбор лучшей модели. 5. Численное оценивание параметров моделей. 6. Получение точечного и интервального прогнозов. 7. Верификация прогноза. Ответ: ___________ 30. Установить правильную последовательность Чаще всего при изучении временных рядов ставятся следующие цели: 1. Краткое описание характерных особенностей ряда. 2. Подбор статистической модели (моделей) для описания того процесса, который мог породить данный временной ряд. 3. Прогнозирование будущих значений на основе прошлых наблюдений. 4. Управление процессом, порождающим временной ряд. Ответ: ___________ 1.4 Практические задания 1. Тема: Расчет коэффициента парной корреляции. Проверка гипотезы об отсутствии линейной связи. План работы. 1. Представьте на точечной диаграмме связь Y с X (точки, не соединенные линиями). 2. Сделайте вывод о форме связи и однородности наблюдений. 3. Выполните расчет ковариации, дисперсии X и дисперсии Y по формулам. 4. Получите коэффициент корреляции по формуле и с помощью функции КОРРЕЛ. 5. Сделайте вывод по знаку коэффициента корреляции. 6. По таблице Чеддока сделайте вывод о тесноте (силе) корреляционной связи. 7. Проверьте гипотезу о равенстве нулю коэффициента корреляции (об отсутствии линейной связи) на уровне значимости 0,05. 8. По данным таблицы 2 получите коэффициент корреляции с помощью функции КОРРЕЛ и выполнить пункты 5-7. Таблица 1 – Источник: Регионы России. Социально-экономические показатели. 2021: Стат. сб. / Росстат. М., 2021. 1242 с. Д 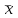 анные 2020 года по Южному федеральному округу анные 2020 года по Южному федеральному округуX 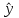 – Среднедушевые денежные доходы населения в месяц, рублей. – Среднедушевые денежные доходы населения в месяц, рублей.Y 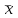 – Общая площадь жилых помещений, приходящаяся в среднем на одного жителя, (на конец года; квадратных метров) – Общая площадь жилых помещений, приходящаяся в среднем на одного жителя, (на конец года; квадратных метров)
Таблица 2 составлена по данным Росстат. Режим доступа https://rosstat.gov.ru/ X – Посевные площади сельскохозяйственных культур по Российской Федерации (хозяйства всех категорий; тысяч гектаров). Y – Валовые сборы сельскохозяйственных культур по Российской Федерации (хозяйства всех категорий; тысяч тонн). Культура – рожь
2. Тема: Парная линейная регрессия. Экономический смысл параметров линейной модели. План работы: 1. Представьте на точечной диаграмме связь Y с X (точки, не соединенные линиями). 2. Запишите систему уравнений МНК с числовыми коэффициентами (см. лекцию). 3. Найдите решение системы уравнений МНК. 4. Найдите параметры модели по формулам МНК (см. лекцию). 5. Поясните экономический смысл коэффициента регрессии. 6. Добавьте полученное уравнение на точечную диаграмму, построенную в пункте 1. 7. Подставив в уравнение заданные значения X, рассчитайте модельные значения ŷ. Для таблицы 2 выполните пункты 1-5. Таблица 1 Источник: Крымстат https://crimea.gks.ru/ X 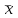 – Число разводов на 1000 человек населения (коэффициент разводимости). – Число разводов на 1000 человек населения (коэффициент разводимости).Y 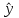 – Число родившихся на 1000 человек населения (коэффициент рождаемости). – Число родившихся на 1000 человек населения (коэффициент рождаемости).
Таблица 2 Источник: Крымстат https://crimea.gks.ru/ (данные 2021 года). X 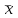 – Число браков на 1000 человек населения (коэффициент брачности). – Число браков на 1000 человек населения (коэффициент брачности).Y 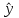 – Число родившихся на 1000 человек населения (коэффициент рождаемости). – Число родившихся на 1000 человек населения (коэффициент рождаемости).
3. Тема: Правило сложения дисперсий. Коэффициент детерминации План работы: 1. Представить на точечной диаграмме связь Y с X (точки, не соединенные линиями). Добавить к диаграмме линию тренда (линейного), показать на диаграмме уравнение и коэффициент детерминации (достоверность аппроксимации). 3. Найти параметры модели регрессии по формулам МНК и сравнить с уравнением на диаграмме. 4. Записать уравнение регрессии и пояснить экономический смысл коэффициента регрессии. 5. Подставить в уравнение заданные значения x и получить модельные значения ŷ . 6. Рассчитать остатки e = y-ŷ. 7. Проиллюстрировать правило сложения дисперсий. 8. Рассчитать коэффициент детерминации и сделать вывод. 9. Рассчитать: дисперсии и среднеквадратические ошибки параметров модели. 10. Проверить гипотезу о равенстве нулю коэффициента регрессии на уровне значимости 0,05. 11. С доверительной вероятностью 0,95 получить границы для истинного значения коэффициента регрессии. Данные – таблица 2 из Задания 2. 4. |