ФОС. ФОС Б1.О.21 Эконометрика БИ. Льтет экономики, управления и юриспруденции Каф
 Скачать 246.92 Kb.
|
|
Тема: Парная линейная регрессия. Применение модели регрессии для прогноза. Доверительные границы для прогноза. План работы: 1. Представьте на точечной диаграмме связь у с x (точки, не соединенные линиями). 2. Добавьте к диаграмме линию тренда (линейного), покажите на диаграмме уравнение и коэффициент детерминации (достоверность аппроксимации). 3. Найдите параметры уравнения линейной регрессии с помощью функции ЛИНЕЙН. 4. Поясните экономический смысл коэффициента регрессии. Поясните смысл коэффициента детерминации. 5. Проверьте гипотезу о статистической значимости коэффициента регрессии по критерию Стьюдента на уровне значимости 0,05. Найдите границы доверительного интервала для коэффициента регрессии с доверительной вероятностью 0,95. 6. Оцените среднюю относительную ошибку точечного прогноза (V). 7. Определите рекомендуемый диапазон ожидаемых значений хр, которые можно подставлять в уравнение регрессии. 8. Подставьте в уравнение значение хp, ожидаемое через 5 лет, получите точечный прогноз и границы доверительного интервала для прогноза с доверительной вероятностью 0,95 (ожидаемое значение x через 5 лет получите по среднему цепному приросту). 9. Добавьте результаты прогнозирования на диаграмму, полученную в п.1. 10. Представите графически границы интервального прогноза для индивидуальных значений y. Для этого задайте 10 произвольных значений xp из рекомендуемого диапазона, постройте таблицу значений точечного прогноза и 95%-го доверительного интервала для прогноза индивидуальных значений y. Представьте точечный прогноз и границы интервального прогноза на диаграмме (точки, соединенные сглаженными линиями). 11.Добавьте к той же диаграмме исходные данные в виде точек. Сколько исходных значений попали в границы найденного прогноза? Соответствует ли это 95%-й доверительной вероятности? Таблица составлена по данным Росстат. Режим доступа https://rosstat.gov.ru/ Данные по хозяйствам всех категорий. Культура – овёс
5. Тема: Парная линейная регрессия. Проверка свойств остатков. Статистические выводы по условиям Гаусса-Маркова План работы: 1. Представить на точечной диаграмме связь Y с X (точки, не соединенные линиями). 2. Добавить к диаграмме линию тренда (линейного), показать на диаграмме уравнение. 3. Определить число наблюдений n с помощью функции СЧЁТ. 4. Найти параметры модели регрессии с помощью функций НАКЛОН и ОТРЕЗОК. 5. Записать уравнение регрессии и пояснить экономический смысл коэффициента регрессии. 6. Подставить в уравнение заданные значения x и получить модельные значения ŷ. 7. Рассчитать остатки e = y-ŷ. 8. Представить на точечной диаграмме связь e с X (точки, не соединенные линиями). 9. Проверить гипотезу о нормальном законе распределения остатков графическим методом. В этом методе значения остатков e сопоставляются с обратной функцией стандартного нормального распределения. Ранг (i) находим с помощью функции РАНГ (категория функций статистические). Первый аргумент функции – текущее значение е, второй – весь массив е (закрепить ссылку), третий аргумент – 0 или 1 по желанию. u – функция НОРМСТОБР. Аргумент – значение (2i-1)/(2n) Представить на точечной диаграмме связь e с u (точки, не соединенные линиями) и сделать вывод по гипотезе. Чем лучше точки ложатся на прямую линию, тем ближе закон распределения к нормальному. 10. Проверить гипотезу о гомоскедастичности (постоянстве дисперсии остатков) по критерию ранговой корреляции Спирмена. Значение |e| – абсолютная величина (модуль) находим с помощью функции ABS (категория функций – математические). 11. Проверить гипотезу о попарной независимости отклонений (отсутствии автокорреляции) по критерию Дарбина-Уотсона. Значения критических точек выбираются для заданного n при m=1. Данные – таблица из задания 4 (с 1990 года по настоящее время) 6. Тема: множественная корреляция. Мультиколлинеарность. План работы. 1. Представить графически связь Y с каждым фактором X. 2. Заполнить корреляционную таблицу с помощью функции КОРРЕЛ. 3. Сделать вывод о наличии мультиколлинеарности. 4. Рассчитать коэффициент детерминации и сделать вывод. 5. Рассчитать частные коэффициенты корреляции Y с каждым фактором X. Сравнить с парными коэффициентами корреляции. Сделать вывод о причине различия.  Источник: Регионы России. Социально-экономические показатели. 2022: Стат. сб. / Росстат. М., 2020. 1122 с. Д 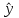 анные 2021 года по Южному федеральному округуY – Потребительские расходы в среднем на душу населения в месяц, рублей/ X1 – Среднедушевые денежные доходы населения в месяц, рублей. X2 – Среднемесячная номинальная начисленная заработная плата работников организаций, рублей. X3 – Стоимость фиксированного набора потребительских товаров и услуг на конец года, рублей. X4 – Соотношение браков и разводов (на 1000 браков приходится разводов)/
7. Тема: Оценка параметров множественной линейной регрессии по методу наименьших квадратов План работы 1. Получить параметры модели множественной линейной регрессии различными способами: а) непосредственно применяя МНК (минимизируя сумму квадратов отклонений с помощью Поиска решения); б) решить систему уравнений МНК матричным методом; в) найти параметры модели с помощью функции ЛИНЕЙН. 2. Записать уравнение регрессии. 3. Проверить гипотезу о равенстве нулю коэффициентов регрессии в генеральной совокупности на уровне значимости 0,05 по критерию Стьюдента. 4. Сделать вывод о статистической значимости коэффициентов регрессии. 5. Пояснить экономический смысл каждого коэффициента регрессии. 6 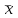. Найти доверительные интервалы для коэффициентов регрессии (доверительная вероятность 0,95).Исходные данные – таблица из Задания 6. 8. Тема: Сравнительный анализ факторов по степени влияния на изменение результативного признака y. План работы. 1. Получить параметры уравнения множественной линейной регрессии и дополнительную статистику с помощью функции ЛИНЕЙН. 2. Записать уравнение регрессии. 3. Сформулировать и проверить гипотезы о равенстве нулю (о статистической незначимости) для каждого коэффициента регрессии на уровне значимости 0,05. 4. При наличии незначимых коэффициентов исключить соответствующие факторы, получить и записать новое уравнение регрессии. 5. Проверить гипотезу о несущественности уменьшения коэффициента детерминации при исключении части факторов. 6. Пояснить смысл каждого коэффициента регрессии в полученном уравнении. 7. Найти доверительные интервалы для истинных значений коэффициентов регрессии с доверительной вероятностью 0,95. 8. Рассчитать: а) Коэффициенты средней эластичности. б) Стандартизованные коэффициенты регрессии (бета-коэффициенты). в) Дельта-коэффициенты. 9. Сравнив между собой рассчитанные в п. 8 коэффициенты, сделать вывод: изменение какого фактора оказывает большее влияние на изменение y. Исходные данные – таблица из Задания 6. 9. Тема: Лаговые переменные. План работы. 1. Представить на одной диаграмме динамику x и y (зависимость от времени). Тип диаграммы – точечная, точки соединены отрезками. 2. Представить в виде корреляционного поля связь y(t) c x(t), связь y(t) c x(t-1), связь y(t) c x(t-2). Тип диаграммы – точечная, точки не соединены. 3. С помощью функции ЛИНЕЙН найти параметры модели 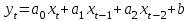 4. Проверить гипотезу о статистической значимости коэффициентов а0, а1 и а2. Уровень значимости 0,05. 5. При наличии незначимых коэффициентов исключить соответствующие факторы и заново применить функцию ЛИНЕЙН. 6. Записать полученное уравнение. 7. Применить полученное уравнение для расчета модельных значений ŷ, включая прогноз на 2023 год. 8. Представить на одном графике динамику y и ŷ (зависимость от времени). Таблица составлена по данным Крымстат. Режим доступа http://crimea.gks.ru Естественное движение населения Y – Родившиеся, человек; X – Зарегистрировано браков, единиц
|