ФОС. ФОС Б1.О.21 Эконометрика БИ. Льтет экономики, управления и юриспруденции Каф
 Скачать 246.92 Kb. Скачать 246.92 Kb.
|
|
10. Тема: Фиктивные переменные. План работы. 1. Представить на одном графике динамику x и y (зависимость от времени). 2. Представить в виде корреляционного поля связь y c x. Тип диаграммы – точечная, точки не соединены. Добавить к диаграмме линию тренда. 3. Найти параметры линейной модели, рассчитать значения ŷ и остатки. 4. Представить на одном графике динамику y и ŷ (зависимость от времени). 5. Представить на графике ряд остатков. Сделать вывод о наличии сезонности. 6. Добавить фиктивные переменные в количестве 11 (январь считать базовым уровнем). 7. С помощью функции ЛИНЕЙН найти параметры модели с фиктивными переменными. 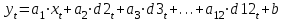 8. Проверить гипотезу о статистической значимости коэффициентов а1, а2,…, a12 на уровне значимости 0,05. 9. При наличии незначимых коэффициентов исключить соответствующие факторы, получить новое уравнение, проверить статистическую значимость коэффициентов 10. Применить полученное уравнение для расчета модельных значений ŷ. 11. Представить на одном графикt динамику y и ŷ (зависимость от времени). Таблица составлена по данным Крымстат. Режим доступа http://crimea.gks.ru X – Среднемесячная номинальная начисленная заработная плата работников по полному кругу организаций, рублей/ Y – Оборот розничной торговли, млн.рублей/
11. Тема: Обоснование и моделирование линейного и полиномиального тренда. План работы. Ознакомьтесь с примерами обоснования выбора моделей и оценки параметров моделей, По аналогии с примерами выполните задание согласно плану: 1. Представить данные графически. Сделать предположение о типе тренда. Добавьте к диаграмме уравнение выбранного вами тренда и прогноз вперед на 2-3 года. 2. Выполнить идентификацию модели (определить степень полинома) по поведению приростов. 3. Найти оценку параметров модели с помощью функции ЛИНЕЙН. 4. Выполнить проверку статистической значимости коэффициента при старшей степени полинома на уровне значимости 0,05. Сделать окончательный вывод о типе модели тренда по трем характеристикам: а) поведение модели на периоде упреждения; б) поведение показателей динамики (приростов); в) статистическая значимость коэффициента при старшей степени полинома. 5. Записать уравнение модели тренда (зависимость y от t). 6. Если тренд линейный, записать экономический смысл коэффициента наклона. Источник данных: Росстат https://rosstat.gov.ru/ Мониторинг развития информационного общества в Российской Федерации Пример 1. Линейный тренд. у – Число музейных предметов, внесенных в электронный каталог, тыс. единиц
Пример 2. Полиномиальный тренд Число доступных в Интернете музейных предметов, внесенных в электронный каталог и имеющих цифровые изображения на 10 000 предметов общего музейного фонда
12. Тема: Прогнозирование по модели полиномиального тренда и по модели простой экспоненты План работы 1. Представить зависимость у от года в виде точечной диаграммы (значения соединены отрезками с маркерами). 2. Добавить справа от столбца y столбец t. 3. Представить зависимость у от t в виде точечной диаграммы (значения соединены отрезками с маркерами). 4. Добавить к диаграмме две линии тренда: полином 2-й степени и экспоненциальную модель. Показать уравнения моделей и добавить прогноз вперед на 3 года. I. Полиномиальный тренд 5. Получить параметры полиномиального тренда с помощью функции ЛИНЕЙН. Для полинома 2-й степени при вызове функции ЛИНЕЙН в качестве Х используют столбцы t и t2. 6. С помощью полученной модели вычислить значения ŷ для данных значений t и на 3 периода вперед ( = 1, 2 3). 7. Получить интервальный прогноз с доверительной вероятностью 0,95 ( = 0,05). Формула для расчета доверительных интервалов прогноза относительно тренда, имеющего вид полинома второго или третьего порядка: 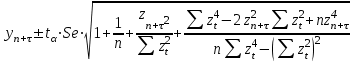 , , 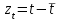 Здесь – период прогнозирования; n – число наблюдений; все суммы от 1 до n; t – критическая точка распределения Стьюдента (найти с помощью функции СТЬЮДРАСПОБР);. Se – среднеквадратичная ошибка модели. II. Экспоненциальный тренд 8. С помощью функции ln (категория Математические) вычислить значения Y=ln(y). 9. Убедиться, что значения Y имеют тренд, близкий к линейному. 10. Найти оценку параметров линейной модели для зависимости Y от t с помощью функции ЛИНЕЙН. 11. Получить модельные значения 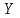 и точечный прогноз на 3 года. и точечный прогноз на 3 года.12. Получить модельные значения 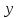 и точечный прогноз на 3 года потенцированием значений и точечный прогноз на 3 года потенцированием значений 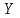 (используем функцию EXP категории Математические). (используем функцию EXP категории Математические).13. Получить интервальный прогноз с доверительной вероятностью 0,95 для Y по формуле для линейного тренда: 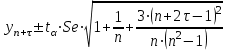 или или 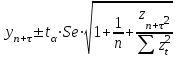 14. Получить интервальный прогноз для y потенцированием границ, полученных для Y. Данные Росстат y – посевные площади под корнеплодные кормовые культуры (включая сахарную свеклу на корм скоту), тыс. га
13. Тема: Построение модели авторегрессии План работы 1. Представляем данные графически с целью предположения о наличии тренда и сезонности. Если тренд отсутствует или близок к линейному, можно приступать к построению АР-модели. 2. Если тренд нелинейный, тренд следует исключить обязательно, если линейный, то желательно. Для исключения тренда переходят к ряду приростов или моделируют тренд и переходят к ряду z=y-T. 3. Построение АР-модели. а) Определяем порядок модели p. Для рядов с сезонностью p равно периоду сезонности. В остальных случаях рассчитываем значения АКФ (автокорреляционной функции) для сдвига k=1, 2, … Максимальное значение k<=[n/4]. Если значения АКФ плавно убывают, рекомендуется рассчитать значения частной автокорреляционной функции (ЧАКФ). б) Находим параметры АР-модели с помощью функции ЛИНЕЙН и проверяем гипотезу о равенстве нулю коэффициентов (о статистической незначимости). При наличии незначимых коэффициентов соответствующие «факторы» исключаем. в) Если модель строили для ряда z, преобразуем в модель для y. 4. Применяем модель для прогноза на 3 года. Когда заканчиваются заданные значения, для прогноза используем смоделированные. Таблица составлена по данным Росстат. Режим доступа http://www.gks.ru у – Посевные площади сельскохозяйственных культур по Российской Федерации (хозяйства всех категорий; тысяч гектаров). Культура – помидоры открытого грунта.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
