математика. Линейная алгебра Вопрос 1 Определение матрицы Матрицей

• Название: Линейная алгебра Вопрос 1 Определение матрицы Матрицей
• Анкор: математика
• Дата: 06.02.2022
• Размер: 258.98 Kb.
• Имя файла: Ekzamen_po_matematike.docx
• Тип: Документы; #353157

Линейная алгебра

Вопрос 1

1. 
   Определение матрицы
   

Матрицей размера m × n называется совокупность mn чисел, расположенных в виде таблицы из m строк и n столбцов: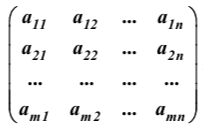

2. 
   Типы матриц
   

• 
  Если в матрице число строк равно числу столбцов, т. е. m = n, то матрицу называют квадратной и в этом случае говорят, что n её порядок.
  
• 
  Остальные матрицы называют прямоугольными.
  
• 
  Квадратная матрица E называется единичной, если все её элементы на главной диагонали равны единице, а остальные равны нулю.
  
• 
  Квадратная матрица называется треугольной, если элементы, стоящие на главной диагонали и над ней, отличны от нуля (не все).
  
• 
  Трапециевидная матрица – прямоугольная матрица, имеющая вид: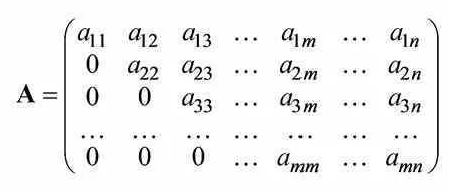
  

• 
  Диагональная матрица – квадратная матрица, элементы только на главной диагонали которой отличны от нуля.
  
• 
  Нулевая матрица – матрица, все элементы которой равны нулю.
  
• 
  Две матрицы называются равными, если они одинакового размера и если равны их элементы, стоящие на одинаковых местах.
  

3. 
   Обозначения матриц
   

Матрицы обозначаются либо одной буквой А, либо А_mxn, либо (а_ij)_mxn.

4. 
   Правила сложения матриц, умножения матрицы на число
   

При сложении (вычитании) матриц одинакового размера складываются (вычитаются) соответствующие элементы:



При умножении матрицы A на число α необходимо на это число умножить все её элементы:

5. 
   Свойства этих операций
   

• 
  k*A=A*k
  
• 
  A+B=B+A
  
• 
  k*(A+B)=k*A+k*B
  
• 
  (k₁+k₂)*A=k₁*A+k₂*A
  
• 
  A+B+C=(A+B)+C=A+(B+C)
  
• 
  A-B=A+(-1)*B
  
• 
  -1*A=-A (Противоположные матрицы)
  
• 
  A+(-A)=0 (Нулевая матрица)
  
• 
  A+-0=A
  

Вопрос 2

1. 
   Умножение матриц
   

При умножении матриц размеры матриц-сомножителей должны быть согласованы: число столбцов первого сомножителя должно равняться числу строк второго, в противном случае умножение невозможно.

Произведением А*B матрицы A = (a_ij)_mxn на матрицу B = (b_ij)_nxk называется матрица C = (c_ij)_mxk, элементы c_ij которой определяются формулой:



Таким образом, чтобы получить элемент cij , стоящий на пересечении i-й строки и j-го столбца, необходимо составить сумму парных произведений элементов i-й строки первой матрицы на элементы j-го столбца второй матрицы: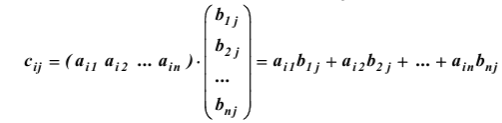

2. 
   Свойства умножения матриц
   

• 
  A*B не равно B*A
  
• 
  A*B=B*A (следовательно, перестановочные матрицы)
  
• 
  A*B*C=(A*B)*C=A*(B*C)
  
• 
  A*(B+C)=A*B+A*C
  
• 
  (A+B)*C=A*C+B*C
  
• 
  k*A*B=(k*A)*B=A*(k*B)
  
• 
  A*E=A
  

E*c=c

Вопрос 3

1. 
   Определение определителя квадратной матрицы 2-го; 3-го порядка
   

Определителем квадратной матрицы 2-го порядка 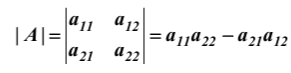называется число, которое записывается и вычисляется так:



Определителем квадратной матрицы 3-го порядка 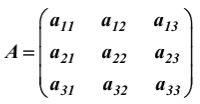называется число, которое записывается и вычисляется так:

2. 
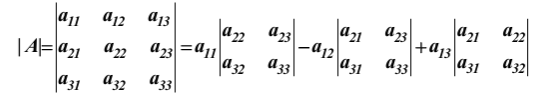   Правило треугольника для вычисления определителя 3-его порядка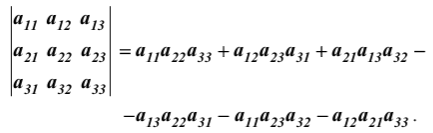
   

Вопрос 4

1. 
   Определение минора и алгебраического дополнения элемента определителя
   

Минор элемента матрицы (M_ij – элемента a_ij) – определитель, который получается из основного определителя вычёркиванием i-ой строчки и j-ого столбца, на пересечении которых стоит элемент a_ij.

Алгебраическое дополнение А_ij элемента а_ij - .

2. 
   Перечислить свойства определителей
   

• 
  Транспонирование – линейная операция, при которой строки матрицы заменяются её столбцами.
  

|А^Т|=|А|

• 
  При перестановке строк/столбцов определитель меняет свой знак.
  
• 
  Если в определителе две одинаковые строки (столбца), он равен нулю.
  
• 
  Если в столбце (строке) есть общий множитель, его можно вынести за знак определителя.
  
• 
  Если в определителе существует нулевая строка (столбец), он равен 0.
  
• 
  Если в определителе есть две пропорциональные строки (столбца), он равен 0.
  
• 
  Если в определителе элементы какой-либо строки (столбца) есть сумма элементов, то определитель равен сумме определителей, где в соответствующей строке (столбце) стоят первые слагаемые, во втором – вторые.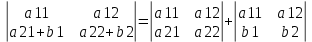
  

• 
  Если к элементам какой-либо строки (столбца) добавить соответствующий элементы другой строки (столбца), умноженные на некоторое число, то определитель не изменяется.
  

При линейной комбинации строк (столбцов) определитель не меняется.

• 
  Определитель может быть вычислен разложением по любой строке (столбцу).
  

Определитель равен сумме произведений любой строки на их алгебраические дополнения.

• 
  Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения другой строки (столбца) равна 0.
  

Вопрос 5

1. 
   Определение обратной матрицы
   

Матpица A⁻¹ называется обpатной к квадратной матрице A, если A⁻¹ ⋅ A = A ⋅ A⁻¹ = E , где E – единичная матрица.

Если |A| ≠ 0 , то обратная матрица может быть найдена по формуле: .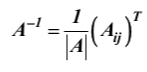

Если |A| = 0 , то матрица А называется вырожденной, и обратной для неё не существует.

2. 
   Теорема о единственности обратной матрицы (с доказательством)
   

Если обратная матрица существует, то она единственная.

Доказательство (от противного):

Пусть существуют матрица А, А₁^-1, А₂^-1.

А* А₁^-1= А₁^-1*А=Е

А* А₂^-1= А₂^-1*А=Е

А₁^-1*А* А₂^-1=(А₁^-1*А)* А₂^-1=Е* А₂^-1= А₂^-1 Следовательно, А₁^-1= А₂^-1

А₁^-1*А* А₂^-1=А₁^-1*(А* А₂^-1)=А₁^-1*Е= А₁^-1

Вопрос 6

1. 
   Теорема о существования обратной матрицы (с доказательством)
   

Обратная матрица существует тогда и только тогда, когда матрица невырожденная (|A|≠0).

Доказательство:

• 
  А^-1 – существует, следовательно, А* А^-1=Е
  

|А* А^-1|=1, следовательно, |А|≠0, |А^-1|≠0, |А^-1|=1/|А|

• 
  Пусть определитель матрицы А отличен от нуля. Докажем, что для матрицы А существует обратная матрица А^-1.
  

Дана матрица:



Найдем транспонированную матрицу: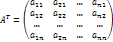



Для каждого элемента матрицы найдем алгебраическое дополнение и составим присоединенную матрицу:



Используя основное свойство алгебраических дополнений, получим:





Получили соотношение:

Тогда . Следовательно, если , то получим , т.е. для невырожденной матрицы А построили обратную матрицу .

2. 
   Сформулировать правило нахождения обратной матрицы
   

• 
  Вычислить определитель матрицы А.
  

Если он равен нулю, то обратно матрицы не существует.

Если отличен от нуля, то:

• 
  Составить матрицу из алгебраических дополнений.
  
• 
  Разделить все элементы полученной матрицы на определитель матрицы А и получить обратную матрицу.
  

Вопрос 7

1. 
   Определение минора k-го порядка матрицы
   

Минор k-ого порядка матрицы А (М_k) – определитель, составленный из элементов, стоящих на пересечении отмеченных k строк и k столбцов.

2. 
   Определение ранга матрицы
   

Рангом матрицы А называется порядок наивысшего отличного от нуля минора матрицы А.

3. 
   Перечислить элементарные преобразования матриц
   

• 
  Перестановка местами двух строк/столбцов.
  
• 
  Умножение строки или столбца на k≠0.
  
• 
  Линейная комбинация строк/столбцов.
  
• 
  Транспонирование.
  
• 
  Вычёркивание нулевых строк (столбцов).
  

4. 
   Сформулировать их основное свойство
   

Элементарные преобразования матриц не изменяют её ранга.

Вопрос 8

1. 
   Определение матрицы трапецевидной формы
   

Трапециевидная матрица – прямоугольная матрица, имеющая вид: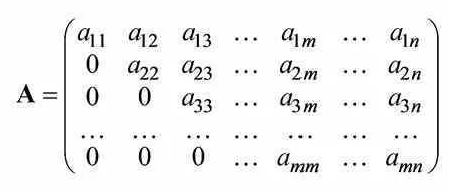

2. 
   Доказать теорему о ранге трапецевидной матрицы
   

Ранг трапецевидной матрицы равен числу ее ненулевых строк .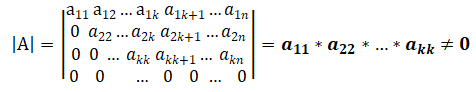



А все остальные миноры большего порядка (если такие в этой трапеции найдутся) содержат нулевую строку, поэтому будут равны 0, значит ранг этой матрицы r(C)=k.

Вопрос 9

1. 
   Понятие СЛАУ (систем линейных алгебраических уравнений)
   

a ₁₁*x₁+ a₁₂*x₂+…+ a_1n*x_n=b₁

a₂₁*x₁+ a₂₂*x₂+…+ a_2n*x_n=b₂

…

a_m1*x₁+ a_m2*x₂+…+ a_mn*x_n=b_m

Где a_ij- коэффиценты системы,

b_i- свободные члены,

x₁, x₂, … , x_n- неизвестные

2. 
   Определение решения СЛАУ
   

Решением системы называется набор чисел с₁, с₂… с_n, которые при подстановки их вместо неизвестных во все уравнения системы обращают эти уравнения в тождества.

3. 
   Типы СЛАУ (совместная, несовместная, определённая, неопределённая, однородная, неоднородная)
   

Система называется совместной, если она имеет решения, и несовместной, если е неё нет решений.

Совместная система называется определённой, если она имеет единственно решение, и неопределённой, если она имеет множество решений.

Система называется однородной, если у неё все свободные члены равны 0 (всегда совместная).

Вопрос 10

1. 
   Теорема Кронекера–Капелли
   

Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы.

2. 
   Теорема о числе решений
   

• 
  Если ранг r совместной системы равен числу неизвестных n, то система имеет единственное решение.
  
• 
  Если r < n, то система имеет бесконечное множество решений. В этом случае r неизвестных являются базисными, а остальные n – r – свободными. Значения свободных неизвестных выбираются произвольно, а значения базисных определяются единственным образом через свободные.
  

Вопрос 11

1. 
   Теорема (правило) Крамера (с доказательством)
   

Если система крамеровского вида (система линейных уравнений называется крамеровской, если в ней число уравнений равно числу неизвестных), |A|≠0 (|A|= Δ-главный определитель системы), то система имеет единственное решение, которое находится по формуле: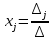

j=1,2,…,n

Δ_j получается из главного определителя системы Δ заменой j-го столбца, столбцом свободных членов.

Доказательство:

Формулы Крамера следуют из матричной формулы ( X=A^-1*B)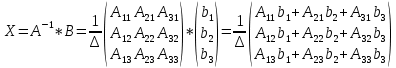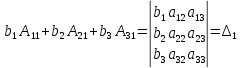



, это формула разложения по 1-му столбцу. Значит, х₁=Δ₁/Δ. Аналогично х₃ и х₂.

Вопрос 12

1. 
   Матричная запись СЛАУ
   

A*X=B

Матрица системы А: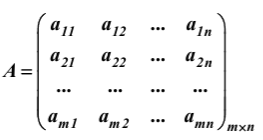



Матрица неизвестных: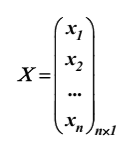



Матрица свободных членов: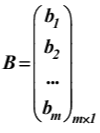



Наряду с матрицей системы А рассматривают также расширенную матрицу системы, получаемую из матрицы А добавлением столбца свободных членов:

2. 
   Матричный метод решения СЛАУ
   

Любая крамеровская система А*Х=В совместна и имеет единственное решение, которое можно найти по формуле: Х=А^-1*В

|A|≠0 => сущ обратная матрица А^-1. Умножаем матричное уравнение А*Х=В слева на А^-1:

А^-1*А*Х=А^-1В, Е*Х=А^-1*В, Х=А^-1*В

Вопрос 13

1. 
   Метода Гаусса решения СЛАУ
   

a ₁₁*x₁+ a₁₂*x₂+…+ a_1n*x_n=b₁

a₂₁*x₁+ a₂₂*x₂+…+ a_2n*x_n=b₂

…

a_m1*x₁+ a_m2*x₂+…+ a_mn*x_n=b_m

Преобразование систем (приводят к эквивалентной системе):

• 
  Перестановка местами двух уравнений.
  
• 
  Умножение левой и правой части на k≠0.
  
• 
  Линейная комбинация уравнений.
  
• 
  Вычёркивание уравнений, у которых правые и левые части равны нулю.
  

Каждое из перечисленных элементарных преобразований, а, значит, и любая их последовательность, переводит линейную систему в эквивалентную.

Элементарные преобразования системы уравнений равносильны элементарным преобразованиям над строками ее расширенной матрицы. Поэтому в дальнейшем описание метода Гаусса будет приводиться с использованием расширенной матрицы.

Как и при вычислении ранга матрицы с помощью элементарных преобразований, будем приводить матрицу к трапецевидной форме. Система уравнений, конечно, изменится, но будет эквивалентной исходной.

Вопрос 14

1. 
   Решение однородных систем
   

Система линейных уравнений называется однородной, если все ее свободные члены равны 0.

Однородная система 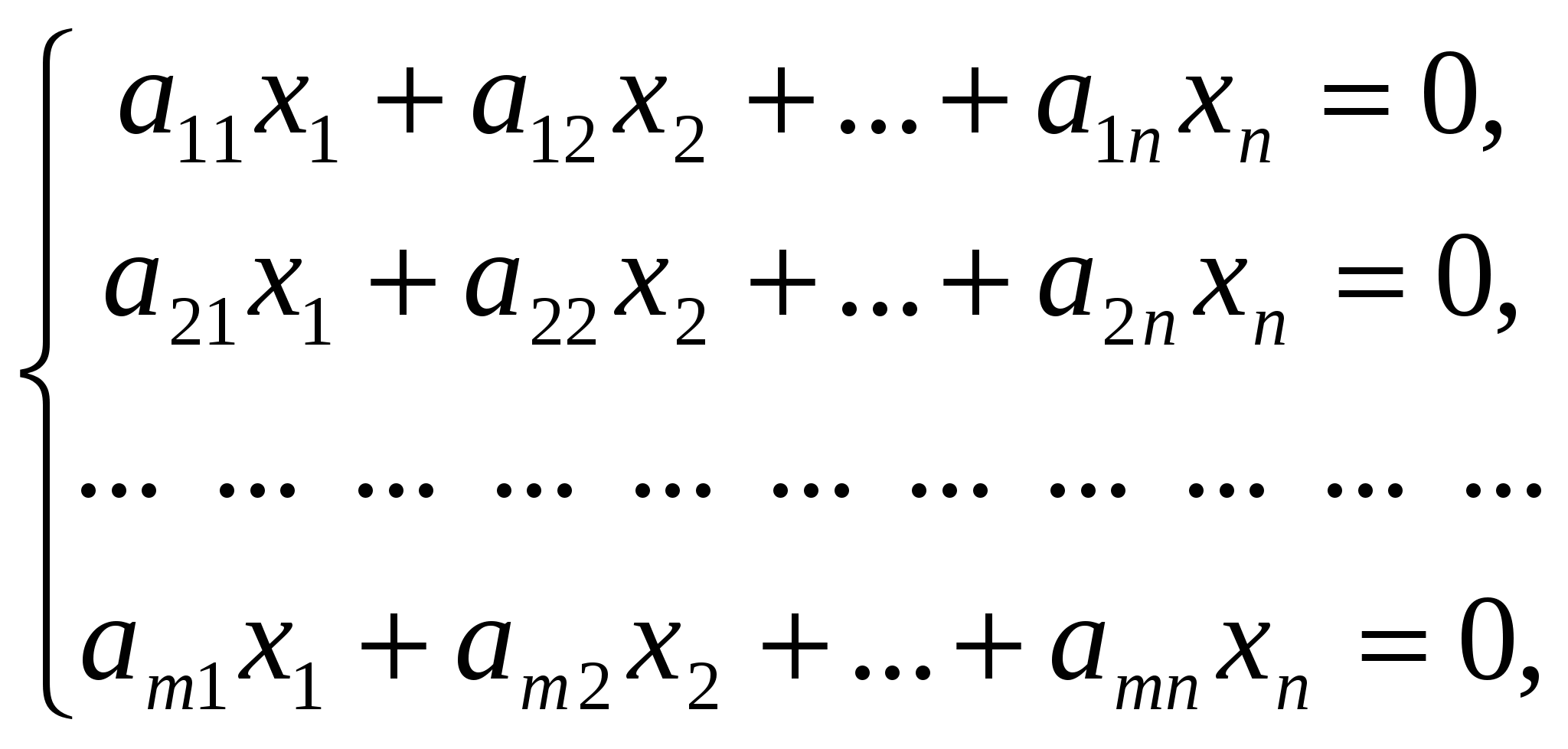линейных алгебраических уравнений с неизвестными представляет собой систему вида



Однородные СЛАУ всегда совместны, поскольку всегда имеется нулевое решение.

2. 
   Сформулировать и доказать условия существования ненулевых решений однородных СЛАУ
   

Однородная система является частным случаем, значит, для нее все справедливо, как и для обычной системы.

• 
  Если r(A)=n (ранг матрицы равен числу неизвестных), то однородная система будет иметь единственное решение - нулевое.
  
• 
  Если r(A)