Линейная функция

• Название: Линейная функция
• Дата: 25.02.2021
• Размер: 0.59 Mb.
• Имя файла: 2_5312040398078610942.doc
• Тип: Решение; #179335

МИНИСТРЕСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН

АНДИЖАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ З.М.БАБУРА



КУРСОВАЯ РАБОТА
По дисциплине: ТФКП

Тема: Линейная функция
Выполнила:

Студентка 4 курса

группа 17– МЕ

Косимова Н. А.

Проверил:

Дж. Дехконов


Содержание

Введение

0. 
   Линейная функция.
   
1. 
   Дробно-линейная функция.
   
2. 
   Степенная функция. Понятие римановой поверхности.
   
3. 
   Показательная и логарифмическая функции.
   
   0. 
      Показательная функция.
      
   1. 
      Логарифмическая функция.
      
   2. 
      Решение примеров.
      
   3. 
      Список литературы.
      

ВВЕДЕНИЕ


Теория функций комплексной переменной (теория аналитических функций) в рамках университетского курса является в основном продолжением курса математического анализа. Основы теории функций комплексной переменной (ТФКП) были заложены в середине XVIII века Л. Эйлером, а как самостоятельная ветвь математики дисциплина оформилась около середины XIX века благодаря работам О. Коши, К. Вейерштрасса, Ю. В. Сохоцкого и Б. Римана. Сейчас ТФКП является одним из важнейших разделов математики. Ее идеи и результаты проникли во многие другие математические дисциплины, такие как алгебраическая топология, обыкновенные дифференциальные уравнения, математическая физика, функциональный анализ, теория вероятностей, вычислительная математика и др. В связи с этим курс ТФКП является обязательным на всех отделениях механико-математического, физического и геологического факультетов.

В последние годы теория функций комплексных переменных получила многочисленные приложения. При этом подходе физические величины рассматриваются как граничные значения функции многих комплексных переменных, голоморфной в некоторой области D, определяемой аксиомами. Но в отличие от одного комплексного переменного в пространстве многих комплексных переменных имеет место явление: не всякая область есть область голоморфности. (В ТФКП из теоремы Римана о возможности конформного отображения произвольной области на единичный круг, который также является областью аналитичности, следует, что всякая область есть область аналитичности.) Поэтому ввиду отсутствия конкретного вида функции возникает задача о построении оболочки голоморфности (множества функций голоморфных) в области D. Далее можно в принципе найти выражение любой функции , голоморфной в D, через её значения на части границы. Если последние значения окажутся связанными с экспериментально наблюдаемыми, то полученное представление открывает путь к экспериментальной проверке теории.

Линейная функция.

Функция w = az + b, (10) , где а и b — заданные комплексные числа и а≠0, называется линейной функцией. Так как w ’ = а ≠ 0, то отображение (10) является конформным во всей плоскости С. Докажем, что оно также однолистно в С. Если w₁ = az₁ + b, w₂ = az₂ + b, то w₁ — w₂ = a(z₁ — z₂). Поэтому при z₁ ≠ z₂ получаем, что w₁ ≠ w₂ , и однолистность установлена. Положив по определению w(∞) = ∞, получим однолистное отображение всей расширенной комплексной плоскости на .

Для изучения геометрических свойств отображения (10) рассмотрим вначале случай b = 0, т.е. w = az. Пусть а = , z = .Тогда

w = .

Поэтому для получения вектора w = az нужно выполнить следующие два действия:

1) умножить заданный вектор z на |а|. При этом направление вектора z останется прежним, но длина увеличится в |а| раз. Значит, умножение на |а| есть преобразование подобия (гомотетия) с центром в начале координат и коэффициентом подобия |а|;

2) повернуть полученный вектор |a|z на угол α.

Для рассмотрения общего случая (10) заметим, что при сложении вектора az с вектором b происходит параллельный перенос концевой точки вектора az на вектор b. Итак, отображение (10) получается путем композиции (т.е. последовательного выполнения) следующих трех операций: 1) преобразования подобия с центром в начале координат и коэффициентом подобия |а|; 2) поворота вокруг начала координат на угол α; 3) параллельного переноса на вектор b.

Дробно-линейная функция.

Перейдем к изучению дробно-линейной функции, определяемой равенством

, (11)

и соответствующего дробно-линейного отображения. Так как

, ,

то естественно определить w(∞) = а/с, w(—d/c) = ∞. Определенная таким образом функция будет непрерывной во всей расширенной комплексной плоскости .

Если с = 0, то w = и дробно-линейная функция сводится к уже изученной линейной функции. Поэтому в дальнейшем предполагается, что с ≠ 0.

Умножим числитель и знаменатель дроби (11) на с и добавим в числителе +ad — ad. Тогда дробь (11) можно представить в виде

. (12)

Если bc — ad = 0, то w = a/c и функция (11) сводится к постоянной. В дальнейшем считаем выполненными условия

с ≠ 0, bc – ad ≠ 0. (13)

Покажем, что дробно-линейная функция (11) осуществляет взаимно-однозначное отображение на . С этой целью решим уравнение (11) относительно z (это возможно при z ≠ —d/c, z ≠ ∞, w ≠ а /с, w ≠ ∞):

.

Поэтому каждое значение w ≠ а/с и w ≠ ∞ имеет только один прообраз z ≠ - d/c и z ≠ ∞. Но в силу определения значению w = а/с соответствует z = ∞, а значению w = ∞ — величина z = —d/c. Итак, каждая точка w имеет только один прообраз z , что и требовалось доказать.

Установим теперь конформность отображения (11). Так как

,

то при z ≠ - d/c и z ≠ ∞ производная w' существует и не равна нулю. По теореме 1 дробно-линейное отображение является конформным всюду, кроме этих двух точек.

Для выяснения конформности при z = - d/c и z = ∞ нам понадобится следующее определение.

Под углом между двумя линиями в точке z = ∞ понимается угол между образами этих линий при отображении w = в начале координат.

Теорема 5. Дробно-линейная функция

, ad — bс ≠ 0, w(∞) = а/с, w(- d/c) = ∞, (14)

осуществляет взаимно-однозначное и конформное отображение расширенной комплексной плоскости на всю .

Мы не исключаем случай с = 0 в теореме 5, так как в этом случае дробно-линейная функция становится линейной, также обладающей всеми свойствами, указанными в теореме 5.

Установим теперь круговое свойство дробно-линейного отображения. Для единообразия дальнейших формулировок удобно рассматривать прямую как окружность бесконечно большого радиуса.

Теорема 6. При дробно-линейном отображении (14) окружности всегда переходят в окружности.

(Заметим, что окружность конечного радиуса может переходить в окружность бесконечного радиуса, т.е. в прямую, и наоборот.)

Доказательство. Рассмотрим уравнение

А(х² +у²) + Вх + Су + D = 0, (15)

где А, В, С, D — действительные коэффициенты. При А = 0 получаем Вх + Су + D = 0, т.е. уравнение прямой. Если А ≠ 0, то, разделив на А и выделив полные квадраты, придем к равенству

(x - x₀)² + (y - y₀)² = ± R²

которое определяет либо окружность, если справа +R², либо точку, если R = 0, либо пустое множество, если справа –R². С другой стороны, любую окружность (в частности, прямую) можно задать уравнением вида (15).

Докажем вначале круговое свойство для отображения w = 1/z. Возьмем произвольную окружность на комплексной плоскости. Она задается уравнением (15). Обозначим z = х + iy, w = u + iv. Равенство w = 1/z дает z = 1/w, или

,

откуда

, .

Чтобы получить уравнение кривой, в которую перейдет окружность при отображении w = 1/z, подставим в (15) найденные выражения для х и у:



или

A + B u – C v + D (u² + v²) = 0

Мы пришли к уравнению такого же вида, что и (15), но в плоскости переменного w = u + iv. Как мы видели ранее, такое уравнение определяет либо окружность (в частности, прямую при D = 0), либо точку, либо пустое множество. Но в силу взаимной однозначности дробно-линейного отображения окружность не может перейти в точку или в пустое множество. Значит, она переходит в окружность и круговое свойство отображения w = 1/z установлено.

Рассмотрим теперь общий случай дробно-линейного отображения (14). Если с = 0, то получим линейное отображение w = a₁z + b₁, которое сводится к растяжению с поворотом и сдвигу. Каждое из этих преобразований, очевидно, обладает круговым свойством. Значит, и для отображения w = a₁z + b₁ данное свойство имеет место.

Пусть теперь с ≠ 0. Воспользовавшись равенством (12), представим дробно-линейное отображение в виде

, (16)

где Е = , F = , G = .

Из равенства (16) следует, что дробно-линейное отображение представлено в виде композиции следующих трех преобразований:

1) w₁ = z + G; 2) w₂ = 1/w; 3) w = E + Fw₂. Как было установлено выше, каждое из этих преобразований окружность переводит в окружность. Значит, их композиция также обладает этим свойством, что и требовалось доказать.

Чтобы сформулировать еще одно свойство дробно-линейных отображений, нам понадобиться следующее определение.

Точки А и А' называются симметричными относительно окружности радиуса R < ∞, если они лежат на одном луче, выходящем из центра О окружности, и

О 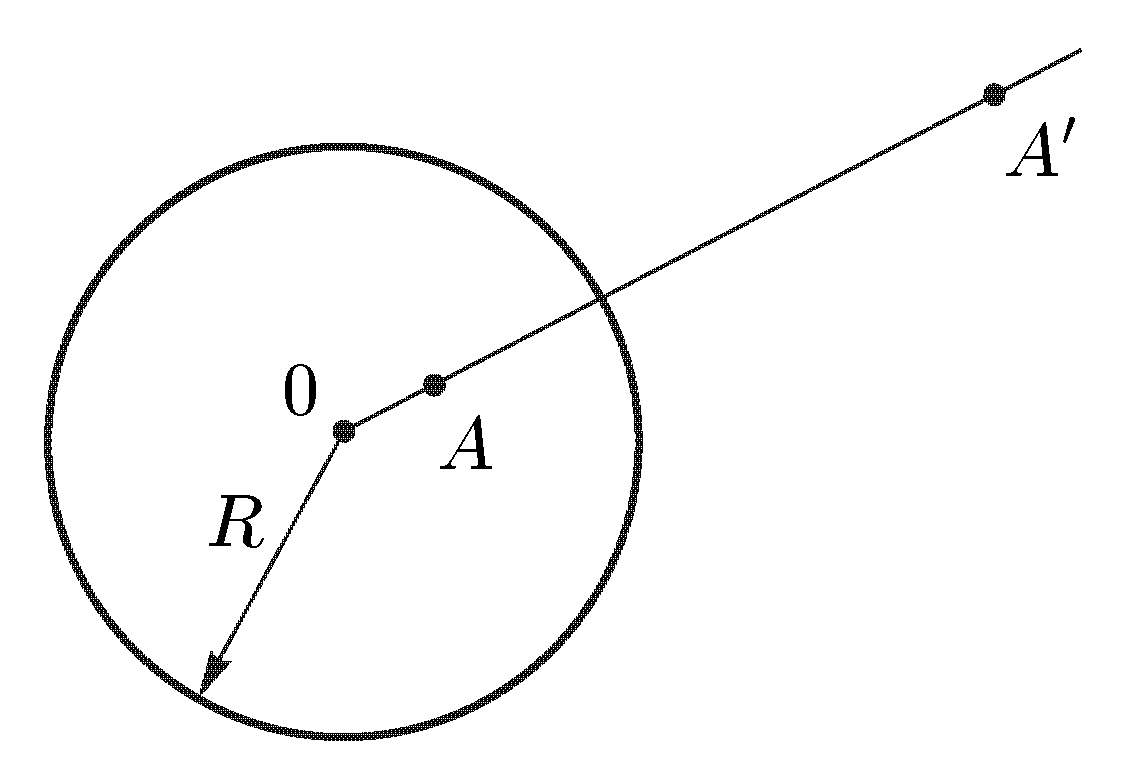А• ОА' = R². (17)

Если точка А приближается к окружности (см. рис. 4), т.е. если ОА → R, то О А' тоже стремится к R; всякая точка на окружности симметрична самой себе; если ОА → 0, то ОА' → ∞. Поэтому для точки О симметричной будет бесконечно удаленная точка. Под симметрией относительно

окружности радиуса R = ∞ понимается (рис. 4) обычная симметрия относительно прямой.

Лемма 7. Для того чтобы точки А и А' были симметричными относительно окружности Г (возможно, бесконечного радиуса), необходимо и достаточно, чтобы любая окружность, проходящая через А и А', была перпендикулярна Г (рис. 5).

Доказательство. Необходимость. Пусть точки А и А' симметричны относительно окружности Г. Проведем произвольную окружность Г ' через точки А и А’ , и пусть В — точка пересечения окружностей Г и Г’. По известной теореме о секущей и касательной произведение секущей ОА' на ее внешнюю часть ОА равно квадрату касательной. В то же время, в силу

с 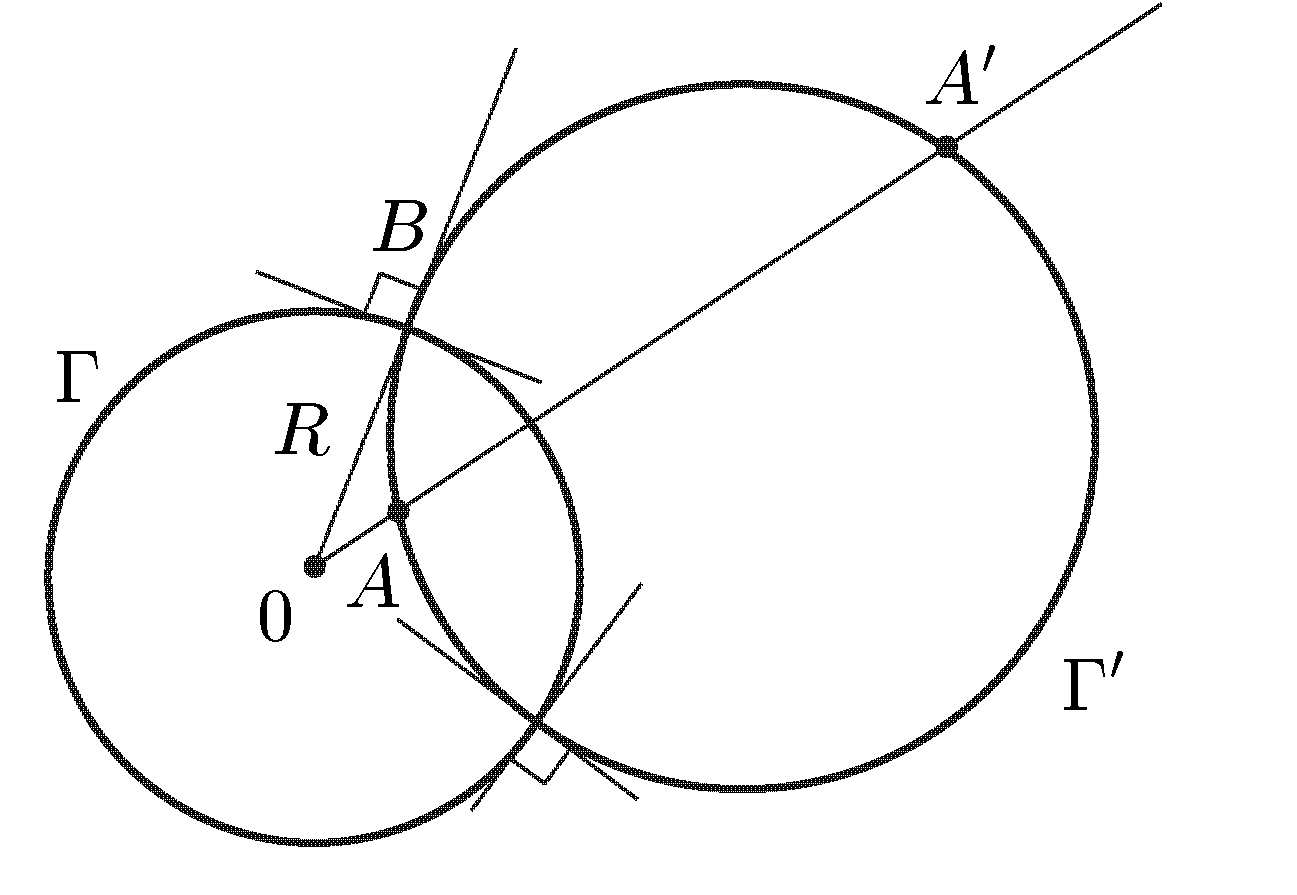имметрии, ОА • ОА’ = R². Значит, (рис. 5)

радиус ОВ является касательной к окружности Г’. Поскольку радиус ОВ перпендикулярен касательной к Г, проходящей через точку В, то окружности Г и Г’ перпендикулярны, что и требовалось доказать. Если Г' — прямая (это будет в случае А = 0), то она проходит через точку О и, следовательно, также перпендикулярна Г.

Достаточность. Пусть точки А и А' таковы, что любая окружность (в частности, прямая), проходящая через них, пересекает Г под прямым углом (см. рис. 5). Докажем, что А и А’ симметричны относительно Г. Так как прямая АА' перпендикулярна Г, то она проходит через точку О. Значит, точки О, А, А' лежат на одной прямой. Но они лежат и на одном луче, выходящем из точки О. Действительно, если бы точки А и А' лежали по разные стороны от точки О, то окружность с диаметром АА' не была бы перпендикулярна Г.

Проведем произвольную окружность Г ' через А и А' с радиусом R’ < ∞. Пусть В — точка пересечения Г и Г’. По условию, Г и Г’ пересекаются под прямым углом. Поэтому радиус ОВ будет касаться Г '. По той же теореме о секущей и касательной ОА • ОА' = R². Следовательно, точки А и А' симметричны относительно Г.

Мы доказали лемму 7 в случае R < ∞. Если R = ∞, то рассуждение существенно упрощается.

Теперь мы готовы установить следующее свойство дробно-линейных отображений (свойство сохранения симметрии):

Теорема 8. При дробно-линейном отображении (14) пара точек, симметричных относительно окружности (в частности, прямой), переходит в пару точек, симметричных относительно образа этой окружности.

Доказательство. Пусть точки z₁ и z₂ симметричны относительно окружности Г. При дробно-линейном отображении (14) Г перейдет в кривую γ, которая по теореме 6 также является окружностью; точки z₁ и z₂ перейдут в точки w₁ и w₂. Надо доказать, что w₁ и w₂ симметричны относительно γ. Возьмем любую окружность γ ', проходящую через w₁ и w₂,и рассмотрим ее прообраз Г ' при отображении (14) (т.е. множество точек на плоскости переменного z, переходящих в γ '). Для этого выразим z из уравнения (14):

при ad – bc ≠ 0

Мы видим, что Г ’ получается из γ’ также дробно-линейным отображением. Поскольку γ ‘ является окружностью, то по теореме 6 Г ‘ — тоже окружность. Так как Г ‘ проходит через точки z₁ и z₂, симметричные относительно Г, то по лемме 7 окружность Г ‘ перпендикулярна Г. В силу конформности дробно-линейного отображения и γ ‘ перпендикулярна γ. По лемме 7 отсюда следует, что точки w₁ и w₂ симметричны относительно γ, и доказательство завершено.

Установленные свойства дробно-линейных отображений позволяют находить отображения областей, ограниченных окружностями (в частности, прямыми).

Степенная функция. Понятие римановой поверхности.

Рассмотрим степенную функцию

w = zⁿ, (18)

где n — натуральное число. Производная w' = nz^n-1 существует и отлична от нуля во всех точках z ≠ 0, z ≠ ∞. Поэтому отображение, осуществляемое функцией (18), является конформным во всех точках, кроме z = 0 и z = ∞. Если записать переменные z и w в показательной форме, z = r e^iφ, w = ρе^iθ, то (18) приводит к равенствам ρ = r ⁿ, θ = nφ.

Отсюда видно, что окружности |z| = r переходят в окружности |w| = r ⁿ, угол 0 < φ < α, где α < 2 π /n, с вершиной в начале координат, лежащий в плоскости переменного z, отображается на угол 0 < θ < nα плоскости w. Следовательно, конформность отображения нарушается в точке z = 0: углы в этой точке увеличиваются при отображении в n раз. Нетрудно показать, что отображение (18) не является конформным и в точке z = ∞.

Пусть точки z₁ и z₂ таковы, что z₂ = z₁ e^{i2 π /n}, n ≥ 2. Легко видеть, что z₁ ≠ z₂ , и . Поэтому отображение (18) не является однолистным во всей комплексной плоскости С, но является таковым внутри любого угла величиной α < 2 π /n с вершиной в начале координат.

Чтобы ввести функцию, обратную степенной, нам нужны следующие определения.

Многозначной функцией комплексного переменного называется правило (закон), по которому комплексному числу z из множества D соответствует несколько (возможно, бесконечно много) комплексных чисел w.

Все функции, рассмотренные ранее (кроме функции Arg z), были однозначными. Функция Arg z является многозначной:

Arg z = arg z + 2πk ,

где arg z — главное значение аргумента и к — любое целое число. В дальнейшем под термином функция, используемым без каких-либо пояснений, подразумевается однозначная функция; многозначность изучаемых функций всегда будет оговариваться дополнительно.

Пусть функция w = f(z) отображает область D на область Е. Обратной к функции w = f(z) называется функция (вообще говоря, многозначная) z = g(w), определенная на области Е, которая каждому комплексному числу w Е ставит в соответствие все комплексные числа z D, такие что f(z) = w.

Другими словами, функция, обратная к w = f(z), — это правило, по которому каждой точке w Е соответствуют все ее прообразы z D.

Если функция w = f(z) однолистна в D, то обратная функция однозначна (и также однолистна) в Е; если w = f(z) не однолистна, то обратная функция будет многозначной. Например, обратной к функции w = zⁿ является многозначная функция z = : каждому значению w, отличному от 0 и ∞, соответствует n различных корней n-й степени, определяемых формулой

(*).

Числа 0 и ∞ имеют по одному корню: , а .

Теорема 9. Пусть функция w = f(z) однолистна и аналитична в области D, отображает D на область Е и f '(z) ≠ 0. Тогда обратная функция z = g(w) также аналитична в области Е и

(19)

Доказательство. Зафиксируем произвольную точку z 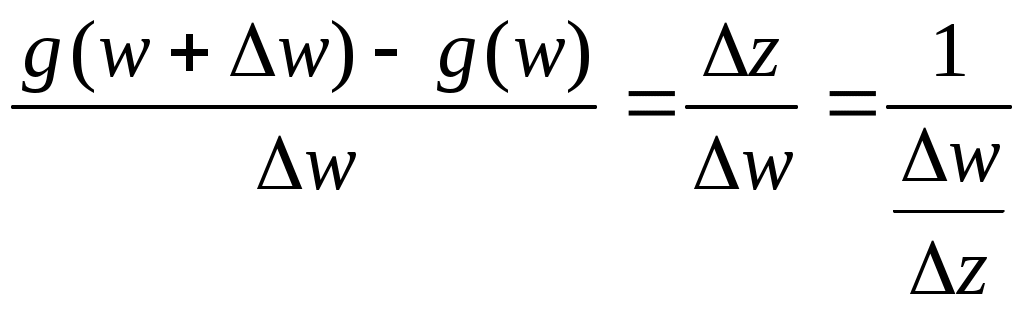D и возьмем приращение Δz ≠ 0. Тогда, в силу однолистности функции w = f(z), соответствующее приращение Δw = f(z + Δz) — f(z) также не равно нулю. Поэтому

Так как функция w = f(z) аналитична, то она непрерывна в точке z.

Следовательно, Δw → 0 при Δz → 0, а в силу взаимной однозначности верно и обратное: Δz → 0 при Δw → 0. Отсюда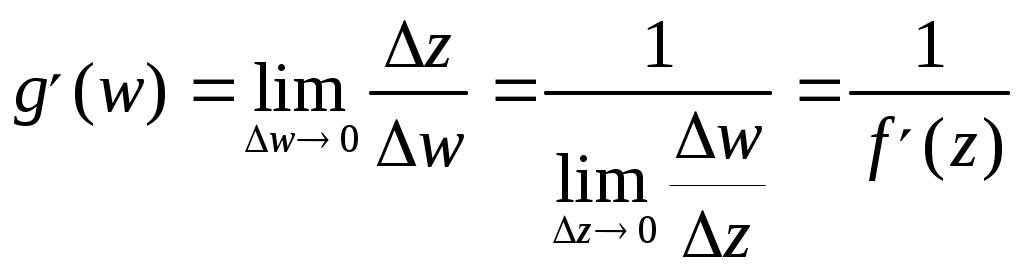



что и требовалось доказать.

Аргументом функции z = g(w), обратной w = f(z), является переменная w. Поскольку аргумент функции часто обозначают через z, то для единообразия переобозначают переменные z и w и пишут w = g(z). Например, обратная функция к w = zⁿ запишется как w = .

Рассмотрим подробнее функцию w = 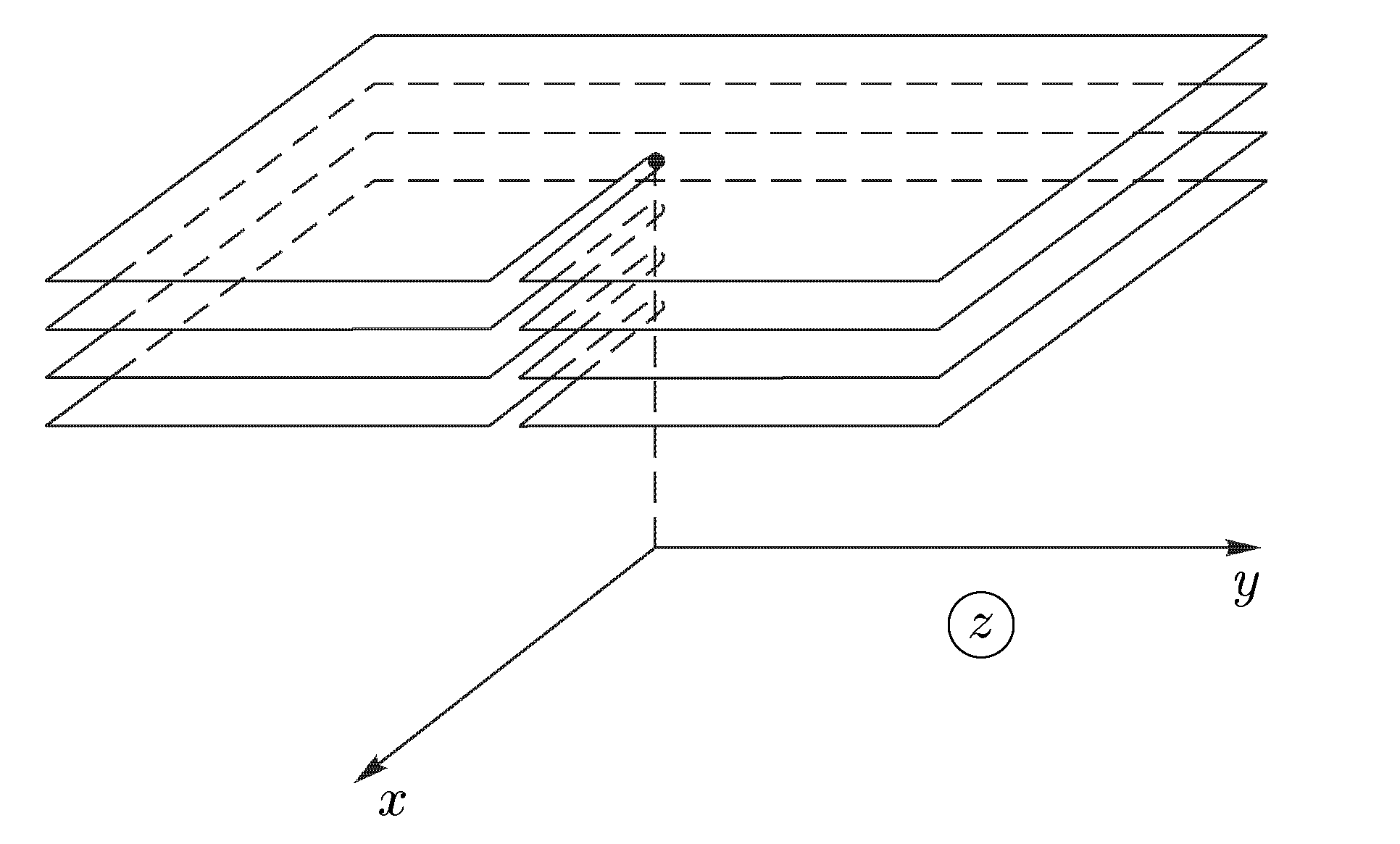. Как было отмечено выше, она является многозначной. Тем не менее можно определить эту функцию на множестве более сложного устройства, чем комплексная плоскость, на котором функция w = станет взаимно-однозначной и непрерывной. Опишем соответствующее множество. Возьмем n экземпляров ("листов") D₀, D₁,..., D_n-1 комплексной плоскости, разрезанной вдоль положительной полуоси, и расположим их друг над другом (на рис. 6а показан случай n = 4).

(рис. 6а)

Затем тот край разреза области D₀, к которому мы подходим снизу от луча ОХ (т.е. по полуплоскости у < 0), склеим с верхним краем разреза области D₁; нижний край разреза области D₁ склеим с верхним краем разреза области D₂ и т.д., пока не склеим нижний край разреза D_n-2 с верхним краем разреза D_n-1. Теперь склеим оставшиеся свободными нижний край разреза области D_n-1 (на рис. 6а это D₃) с верхним краем разреза области D₀. В трехмерном пространстве такую склейку невозможно осуществить без пересечения с уже сделанными склейками промежуточных листов. Но мы условимся считать эту склейку непересекающейся с предыдущими (т.е. точки этой склейки считаются отличными от точек остальных склеек). Полученная поверхность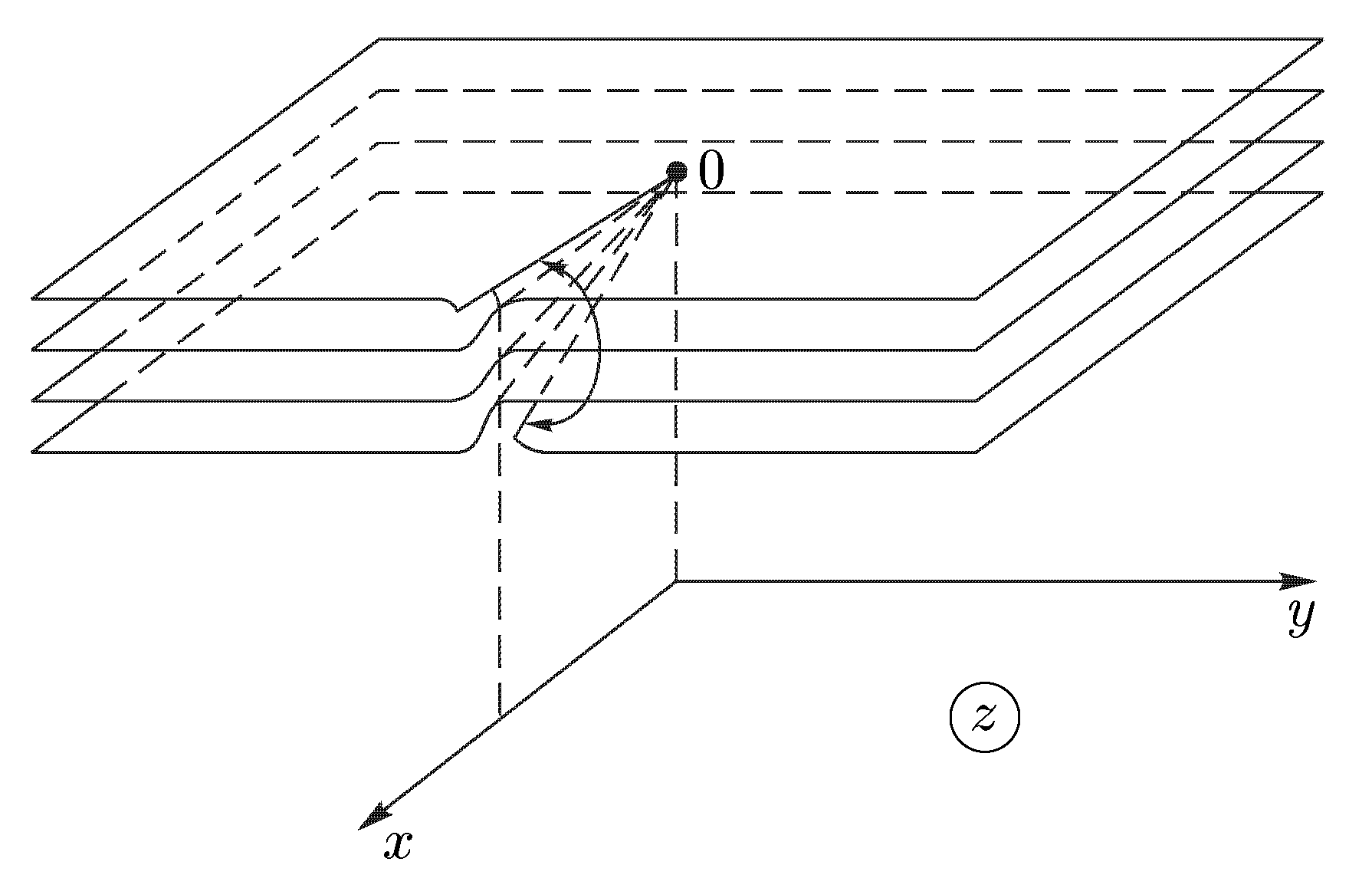

(рис. 6б)

показана на рис. 6б. Она называется римановой поверхностью функции w = . Над каждой точкой комплексной плоскости, отличной от 0 и ∞, расположено ровно n точек римановой поверхности. Точки х > 0 действительной полуоси не составляют исключения, так как все склейки, расположенные над ней, считаются непересекающимися. Лишь две точки не обладают этим свойством: z = 0 и z = ∞.Все листы римановой поверхности считаются склеенными в точках, расположенных над точками z = 0 и z = ∞.

Определим теперь функцию w = на построенной римановой поверхности. Напомним, что если z = r e^iφ, то все корни n-й степени из z определяются формулой (*):

(20)

Угол φ в этой формуле можно выбирать из любого промежутка длины 2π; нам удобно предполагать, что 0 ≤ φ < 2π.

Точкам z = r e^iφ, лежащим на листе D₀ и склейке D₀ с D_n-1, ставим в соответствие значение корня с k = 0; точкам, лежащим на листе D₁ и склейке D₁ с D₀, — значение корня с k = 1. Вообще, точкам, лежащим на D_k, при 1 ≤ k ≤ n-1, и склейке D_k, с D_k-1, соответствует значение корня с данным k. Построенное соответствие будет однозначной функцией на римановой поверхности.

Нетрудно показать, что эта функция взаимно-однозначно отображает риманову поверхность на всю комплексную плоскость. Действительно, лист D_k будет отображаться в угол , а склейки отобразятся в лучи, соединяющие эти углы; тем самым вся комплексная плоскость будет покрыта образами точек римановой поверхности.

Покажем, что это отображение является и непрерывным. Если точка z лежит на листе D_k с разрезом, то непрерывность в этой точке прямо следует из формулы (20) с фиксированным к. Для демонстрации непрерывности в точках склеек рассмотрим контур на римановой поверхности, состоящий из точек, расположенных над окружностью |z| = 1 комплексной плоскости. Начнем обходить этот контур с точки z, расположенной на верхнем крае разреза листа D₀. Так как r = 1, φ = 0, k = 0, то w = = 1. При обходе первого витка контура на листе D₀ будет

и . Перейдя по склейке на лист D₁, мы получим, по определению, (так как к = 1). В частности, при φ = 0 будет то же самое значение корня, к которому мы приближались, подходя к нижнему берегу разреза по листу D₀. Значит, в точках склейки D₀ c D­₁ функция будет непрерывной. Аналогично показывается непрерывность корня и при переходе с D_k-1 на D_k при 1 ≤ k ≤ n-1. Наконец, обходя контур по листу D_n-1 и приближаясь к нижнему краю разреза, получим k = n - 1, , и ,

т.е. то самое значение, с которого мы начинали на верхнем крае разреза листа D₀. Таким образом, функция будет непрерывной во всех точках римановой поверхности. Как функция, обратная к аналитической, она является также однозначной аналитической функцией на этой поверхности (кроме точек z = 0 и z = ∞).

Возьмем любую окружность |z| = r на комплексной плоскости, охватывающую точку z = 0. Эта окружность будет охватывать также и точку z = ∞. Обходя контур на римановой поверхности, состоящий из точек, расположенных над этой окружностью, мы будем переходить с одного листа римановой поверхности на другой. Поэтому точки z = 0 и z = ∞ называются точками ветвления. Ни одна другая точка описанным свойством не обладает: если взять окружность с центром в точке z ≠ 0, z ≠ ∞, не содержащую внутри себя точку 0, то соответствующие точки на римановой поверхности образуют n окружностей, не связанных друг с другом. Обходя каждую из них, мы не выйдем за пределы одного и того же листа.

Однозначная аналитическая в области D функция f (z) называется регулярной ветвью многозначной функции F (z), определенной в этой же области, если значение f (z) в каждой точке z области D совпадает с одним из значений F (z) в этой точке.

Многозначная функция F (z) является однозначной и аналитической на своей римановой поверхности (за исключением точек ветвления). Поэтому возможность выделить в области D регулярную ветвь означает возможность расположить эту область на римановой поверхности, не разрезая D и не задевая точек ветвления. Область D должна при этом целиком укладываться на одном листе или спускаться по склейке с одного листа на другой (как ковер по лестнице). Например, кольцо 1 < |z| < 2 нельзя без разрывов расположить на римановой поверхности функции F (z) = , n ≥ 2, поскольку точки кольца, располагаемые над положительной полуосью, должны одновременно попасть на разные листы, что невозможно. Но если разрезать кольцо по любому радиусу, то такое расположение становится возможным. При этом расположить D на римановой поверхности можно n способами (и, следовательно, выделить в D n различных ветвей функции ). Для выделения конкретной ветви достаточно указать значение функции в какой-либо точке области D. Тем самым указывается лист римановой поверхности, на который попадает эта точка, а значит, фиксируется расположение и всей области D.

Показательная и логарифмическая функции

1. Показательная функция e^z определяется следующими соотношениями: для любого комплексного числа z = х + iу

e^z = e^{x + iy} = e^x(cos y + i sin y). (21)

Второе равенство в (21) получается, если принять по определению е^{х + iу} = е^хе^iу и применить к е^iу формулу Эйлера . Из (21) следует, что

|e^z| = |е^x+iу| = е^x, Arg e^z = у + 2 πn.

Определение (21) и свойства функции е^iφ позволяют легко доказать, что функция e^z обладает обычными свойствами показательной функции:

e^z1+z2 = e^z1e^z2; e^{z1 – z2} = e^z1/e^z2; (e^z)ⁿ = e^nz.

Докажем, что функция e^z будет аналитической во всей комплексной плоскости С. Для этого надо проверить выполнимость условий Коши—Римана (7). Если w = u + iv, то в силу (21) u + iv = е^х cos у + iе^х sin у, откуда u = е^х cos у, v = e^x sin y;



Таким образом, условия (7) выполнены, и аналитичность функции e^z доказана. Чтобы вычислить производную (e^z)’, воспользуемся независимостью производной от направления и вычислим производную в направлении оси ОХ:

.

Следовательно, для производной функции e^z имеет место обычная формула

(e^z)’ = е^z .

Следующее свойство функции e^z не имеет аналога в случае показательной функции действительного переменного: функция e^z является периодической с чисто мнимым периодом 2πi. В самом деле, для любого целого n

e^{z +2πni} = e^x(cos(y + 2πn) + i sin(у+2πn)) = е^x(cos y + i sin y) = e^z.

Из периодичности функции w = e^z следует, в частности, что она не является однолистной во всей комплексной плоскости. Для выяснения, в каких областях эта функция однолистна, положим z₁ = x₁ + iy₁, z₂ = х₂ + iy₂. В силу (21), равенство e^z1 = e^z2 равносильно следующим условиям:

e^x1 = e^x2, cos y₁ = cos y₂, sin y₁ = sin y₂,

откуда следует х₁ = x₂, y₁ = y₂ + 2πn, где n — произвольное целое число, или

z₁ – z₂ = 2πni. (22)

Следовательно, для взаимной однозначности отображения w = e^z в области D необходимо и достаточно, чтобы D не содержала никакой пары точек, для которой справедливо (22). В частности, этому условию удовлетворяет любая горизонтальная полоса шириной 2π, например полосы

{z : - ∞ < х < ∞, 2πk < у < 2 π(k + 1)}, k = 0, ±1, ±2,...

Каждой такой полосе соответствует совокупность значений w = e^z = e^xe^iy = ρe^iθ для которых, в силу равенств ρ = е^х, θ = у, имеем

0 < ρ < ∞, 2πk < θ < 2π(k + 1).

Эти значения w заполняют всю комплексную плоскость переменного w с разрезом по действительной положительной полуоси. При этом прямые у = у₀ (показаны на рис. 7, а пунктиром) переходят в лучи θ = у₀ (рис. 7б), а интервалы x = x₀, 2πk< у < 2π(k + 1) (показаны сплошными линиями 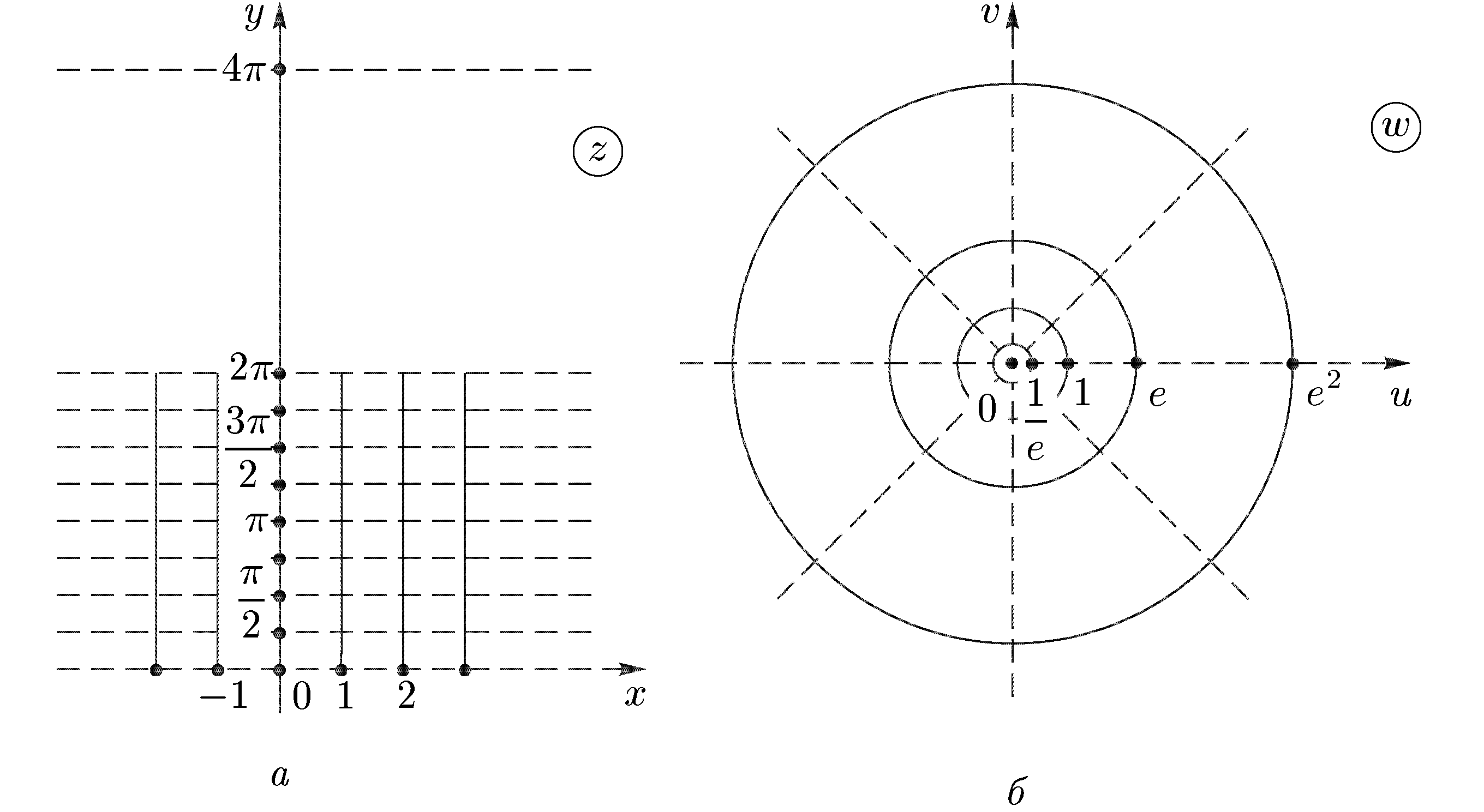(рис. 7)

для k = 0) — в окружности ρe^x0 (с выколотыми точками на полуоси u > 0). Полосы 0 < Im z < h < 2 π показательная функция e^z отображает в углы 0 < θ < h. В частности, полоса 0 < Im z < π переводится в верхнюю полуплоскость.

2. Логарифмической функцией называется функция, обратная показательной.

Так как показательная функция e^z не является однолистной в С, то обратная к ней функция будет многозначной. Эта многозначная логарифмическая функция обозначается Ln z. Таким образом, если w = Ln z, то z = e^w. Положим

w = u + iv, z = r e^iφ = re^{iArg z}.

Тогда

re^{iArg z} = z = e^w = e^{u + iv} = e^ue^iv.

Сравнивая числа, стоящие в начале и конце этой цепочки, заключаем, что

r = e^u, e ^{i Arg z} = e^iv. (23)

Из первого равенства находим u = ln r, где ln r — обычный натуральный логарифм положительного числа r. Второе равенство в (23) дает v = Arg z. Таким образом,

Lnz = ln |z| + i Arg z. (24)

Каждому комплексному числу z, отличному от 0 и ∞, формула (24) ставит в соответствие бесконечное множество значений Ln z, отличающихся друг от друга на величину 2 πki, где k — любое целое число. Удобно представить Arg z в виде

Arg z = arg z + 2 πk, - π < arg z ≤ π,

где arg z — главное значение аргумента. Тогда формула (24) примет вид

Ln z = ln |z| +i(arg z + 2πk ). (25)

Для каждого значения k функция Ln z является непрерывной однозначной функцией в комплексной плоскости с разрезом по отрицательной полуоси; она также и аналитична в этой области как функция, обратная аналитической функции e^z. Таким образом, для каждого фиксированного k формула (25) определяет регулярную ветвь многозначной функции Ln z. Эта ветвь взаимно-однозначно отображает плоскость с разрезом по отрицательной полуоси в полосу

- π + 2 πk < Im w < π + 2πk.

Ветвь, которая получается при k = 0, обозначается ln z и называется главным значением многозначной функции Ln z:

ln z = ln |z| + i arg z.

Н 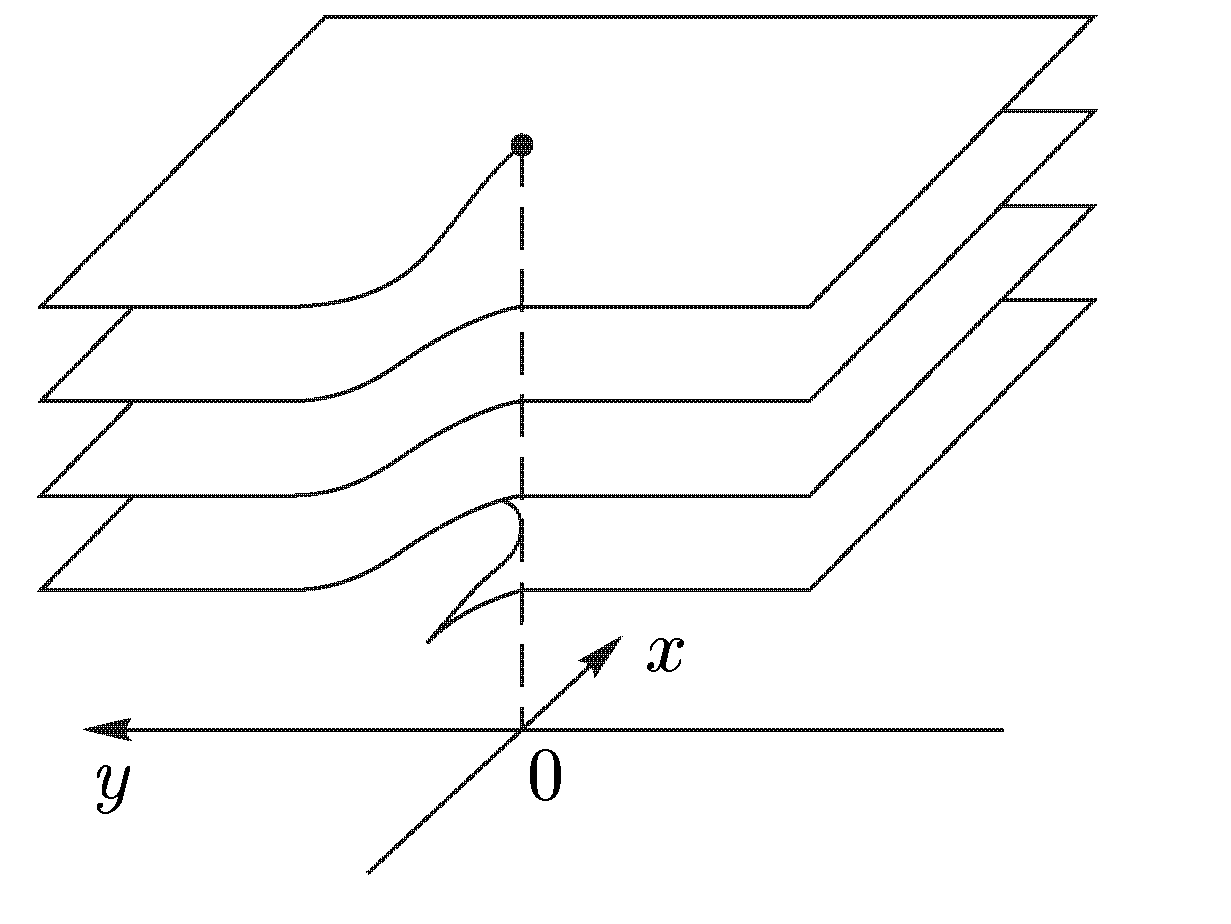апример, ln i = ln 1 + iπ/2 = iπ/2; ln(-i) = ln 1 — iπ/2 = —iπ/2. Если приближаться к точке z = — 1 по верхней полуплоскости у > 0, то ; если по нижней, — то .

Чтобы представить себе риманову поверхность функции Ln z, возьмем бесконечное количество экземпляров ("листов") плоскости с разрезом по отрицательной полуоси и склеим их так, как показано на рис. 8. Над каждой точкой плоскости, кроме точек z = 0 и z = ∞,

располагается бесконечно много точек (рис. 8)

римановой поверхности. В точках 0 и ∞ функция Ln z не определена, и точек поверхности над ними нет. Точки z = 0 и z = ∞ называются точками ветвления бесконечного порядка.

Рис. 8 наглядно демонстрирует причину того, что : если предположить, что точки — 1 ± h, h > 0, находятся на одном и том же листе римановой поверхности и устремить h, к нулю, то предельные положения этих точек окажутся на разных листах римановой поверхности.

Выделить регулярную ветвь логарифма можно не только в области D, являющейся плоскостью с разрезом по отрицательной полуоси. Если сделать разрез плоскости по любому лучу, то полученная область также допускает выделение в ней регулярной ветви. Пусть разрез сделан по лучу, идущему под углом θ к оси ОХ. Тогда регулярные ветви будут задаваться следующей формулой: при z = e^iφ

Ln z = ln r + i(φ + 2πk), θ < φ < θ + 2 π.

Формула (25) является частным случаем при θ = - π. Производная каждой регулярной ветви f (z) логарифма находится по формуле , аналогичной формуле для производной логарифмической функции действительного переменного. Этот факт выводится из равенства (e^z)’ = e^z и формулы (19) производной обратной функции. Действительно, обратной к w = f(z) будет функция z = e^w. Отсюда и из (19) получаем

.

Решение примеров

Пример 4.5 ([3], № 2.1). Найти целую линейную функцию (т.е. функцию вида w = az +b , где a и b комплексные постоянные), отображающую треугольник с вершинами в точках 0 , 1, i на подобный ему треугольник с вершинами 0 , 2 , 1 + i (рис. 4.6 и 4.7).

Решение. В соответствии с геометрическим смыслом преобразования, осуществляемого линейной функцией, точка z = 0 (вершина прямого угла треугольника в плоскости z ) переходит в точку w =1 + i (вершина прямого угла образа этого треугольника в плоскости w ): 1 + i = a 0 +b b =1 +i .

Вершина z = i переходит в вершину w = 2 2 = a i +1 + i ; ai =1 − i; a = −i −1 w = (1+i)(1− z) .

Пример 4.6 ([3], № 2.6). Найти целую линейную функцию w(z), отображающую полосу, заключенную между прямыми х = а

и x = a + h на полосу 0 < u <1 при указанной нормировке: w (a) = 0 .

Решение. В силу принципа соответствия границ при конформном отображении, граница исходной области переходит в границу отображения этой области. Чтобы внутренность исходной области переходила во внутренность отображения, дается условие, в данном случае w (a) = 0 .

Общий вид целой линейной функции w = cz + d . Пусть прямая х = а переходит в прямую u = 0 , тогда iυ = c (a +iy) + d .

Прямая x = a + h переходит в прямую u =1 , тогда

1 +iυ = c (a + h +iy) + d 1 = ch c = h1 w = h1 z + d .

Используем условие w (a) = 0 :

0 = h1 a + d d = − ah w = h1 (z − a ) .

Пример 4.7 ([3], № 2.7). Найти целую линейную функцию, отображающую круг z < 1 на круг w − w0 < R так, чтобы центры

кругов соответствовали друг другу и горизонтальный диаметр переходил в диаметр, образующий с направлением действительной оси угол α.

Решение. По смыслу линейного преобразования, изменим диаметр круга с 1 на R преобразованием w1 = Rzeiα, сохранив центр

круга в начале координат и повернув горизонтальный диаметр на угол α против часовой стрелки. Затем осуществим преобразование параллельного переноса так, чтобы центр круга z= 0 перешел в

центр круга w = w0 : w2 = w1 + w0 . Окончательно: w = eiαRz + w0 .

ЗАКЛЮЧЕНИЕ

Как и предполагалось, при обобщении соответствующих понятий для функций комплексных переменных были получены некоторые идейные расхождения, которые до поры до времени не прослеживаются в силу аналогичности определений. Основной причиной этого для обобщения из ТФКП служила переопределённость условий Коши-Римана, для функций многих действительных переменных – введенная асимметрия вещественного пространства.

Список литературы.

1. Эйдерман В. Я. «Основы теории функций комплексного переменного и операционного исчисления.»

2. Свешников А. Г., Тихонов А. Н. «Теория функций комплексной переменной»

3. Михайлов В.Д. «Теория функций комплексной переменной» Практикум

4. Билута П. А. Лекции по теории функций комплексного переменного.

Новосиб. гос. ун-т. Новосибирск, 2005.

5. Волковыский Л. И., Лунц Г. Л., Араманович И. Г. Сборник задач по теории функций комплексного переменного. М.: Физматлит, 2002.

6. Привалов И. И. Введение в теорию функций комплексного переменного. М:, Физматгиз, 1960.

7. Чуешев В. В., Чуешева Н. А. Справочное пособие по теории функций комплексного переменного. Кемерово, 1993, Ч. I-III.