Тесты по математике 2курс1. Линейных уравнений называется совместной, если она

• Название: Линейных уравнений называется совместной, если она
• Дата: 25.01.2023
• Размер: 0.88 Mb.
• Имя файла: Тесты по математике 2курс1.doc
• Тип: Решение; #903897
• страница: 4 из 6

Какое из следующих утверждений ложно?

1) А  А ^–1 = А^-1  А = Е ;

2) если а₁₁ а₂₂ – а ₁₂ а₂₁ 0 ,то существует обратная матрица А^-1;

3) если а₁₁а₂₂ – а₁₂а₂₁ = 0 , то для А найдется обратная ей матрица А^-1.

4) А= ;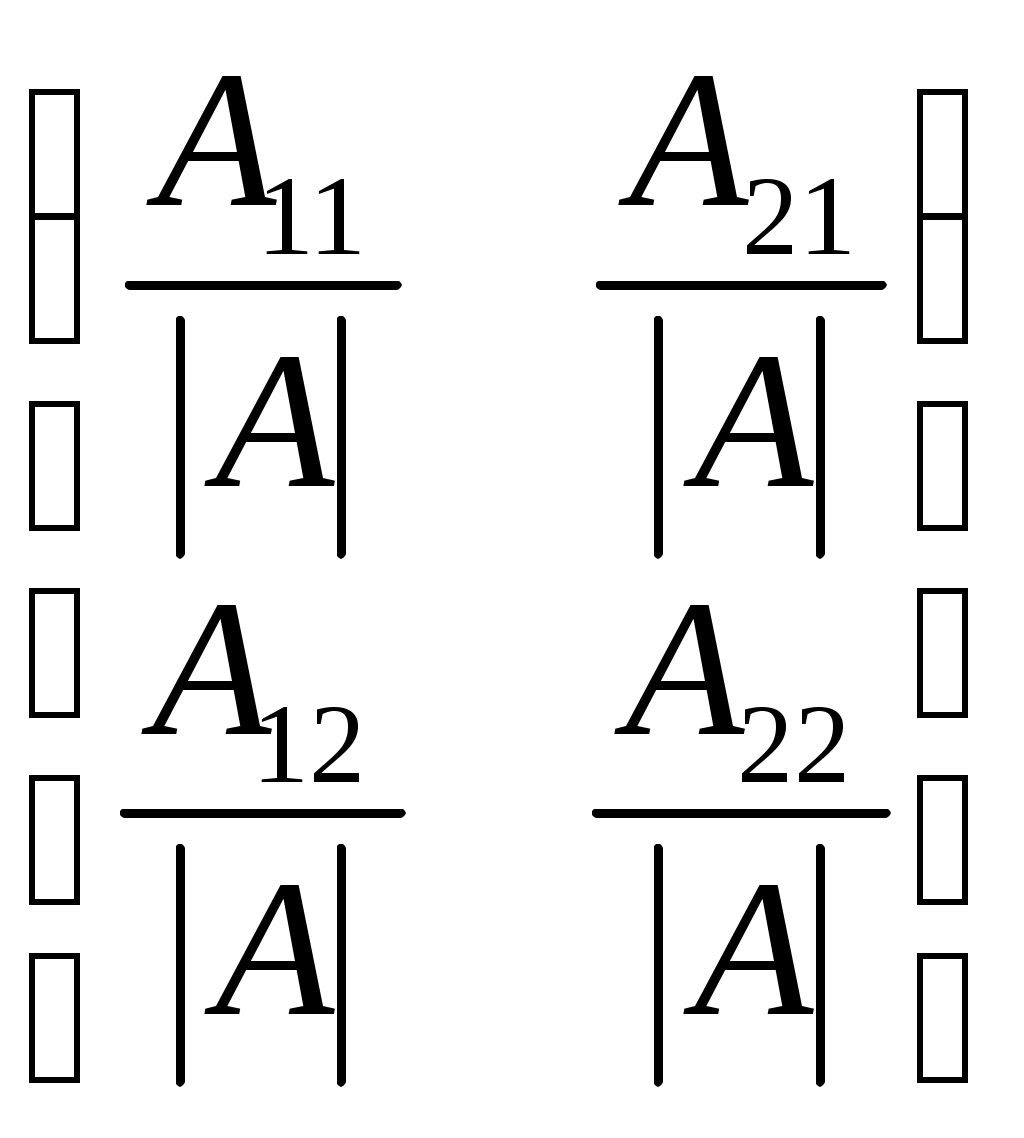

5) А^-1Е =А^-1.

3

Решение системы в матричной форме: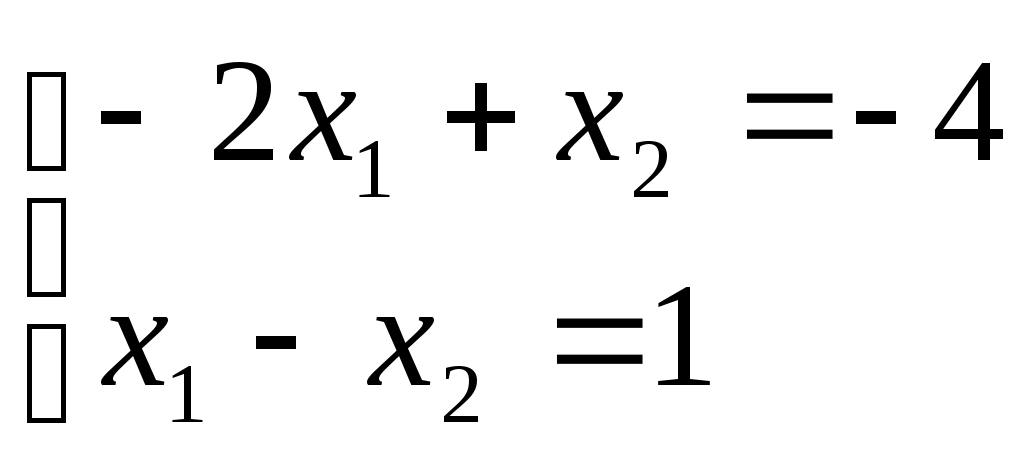

А= ; В = ; X= .

1) Х=А^-1 В;

2) Х=АВА^-1;

3) Х=АВ;

4) не имеет решения;

5) Х=А^-1В А.

1

Вычислить определитель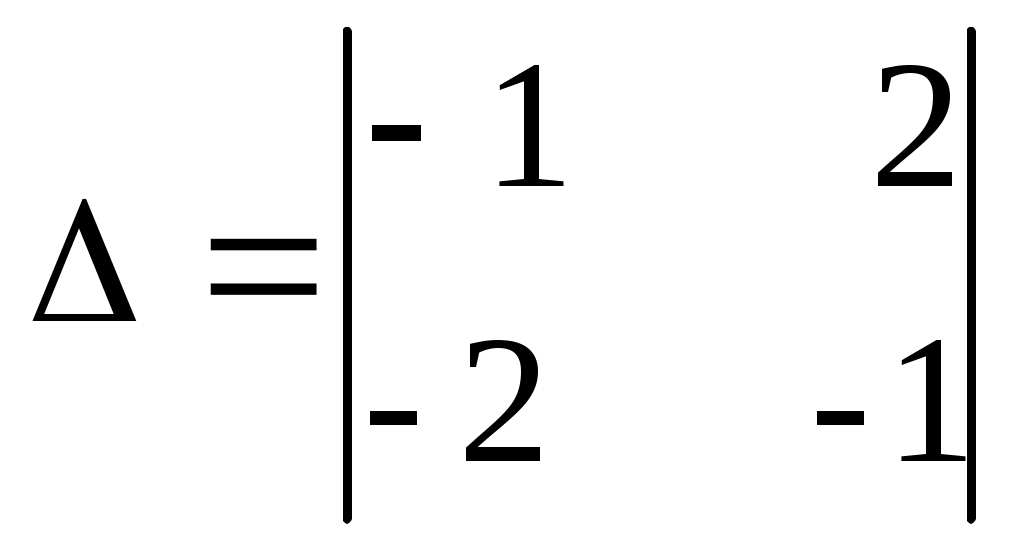

1) 5

2) -3

3) 3

4) 0

5) -5

1

Найти ранг матрицы

1) 2;

2) 3;

3) 1;

4) 0;

5) 4.

2

Общее уравнение прямой на плоскости

1) Ах + Ву + С = 0;

2) ;

3) у = kx + b;

4) у – у₁ = k (x – x₁) ;

5) .

1

Уравнение прямой с угловым коэффициентом

1) Ах + Ву + С = 0;

2) ;

3) у = kx + b;

4) у – у₁ = k (x – x₁) ;

5) .

3

Уравнение прямой проходящей через данную точку в данном направлении

1) Ах + Ву + С = 0;

2) ;

3) у = kx + b;

4) у – у₁ = k (x – x₁);

5) .

4

На плоскости, что определяет формула ?

1) Скалярное произведение векторов х и у;

2) Длину векторов х и у;

3) Угол между векторами;

4) Косинус угла между векторами х и у;

5) Синус угла между векторами х и у.

4

Найти угол между векторами ; .

1) 30⁰;

2) 60⁰;

3) 0⁰;

4) 90⁰;

5) 45⁰.

4

Условие перпендикулярности прямых ,

1) 

2) 

3) 

4) -  - 

5) -  - 

1

Уравнение прямой, проходящей через две данные точки

1) Ах + Ву + С = 0;

2) ;

3) у = kx + b;

4) у – у₁ = k (x – x₁) ;

5) .

2

Вычислить А*В, если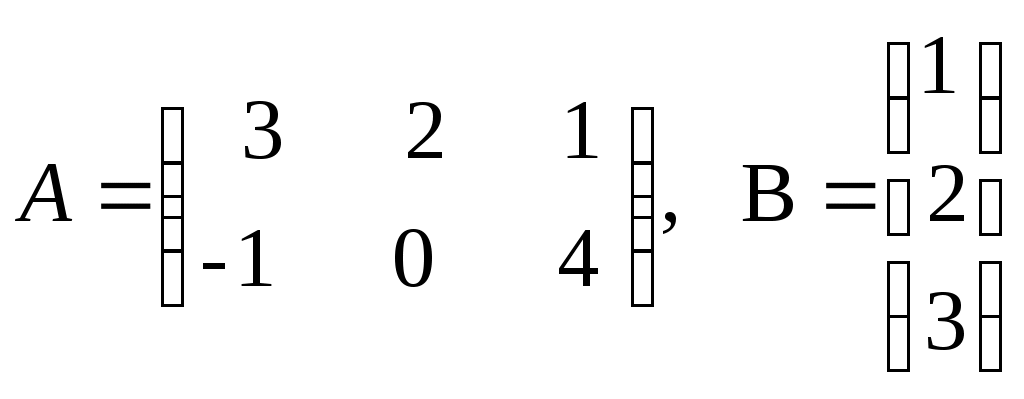

1)

2)

3) (10 11)

4)

5)

4

Формула расстояния между точками ,

A) d x -x -y -y 

B) d  

C) d  

D) d  

E) d  

5

Найти расстояние от точки -3 4 до оси Ох

1) -3

2) 4

3) 25

4) 7

5) 1

2

Вычислить определитель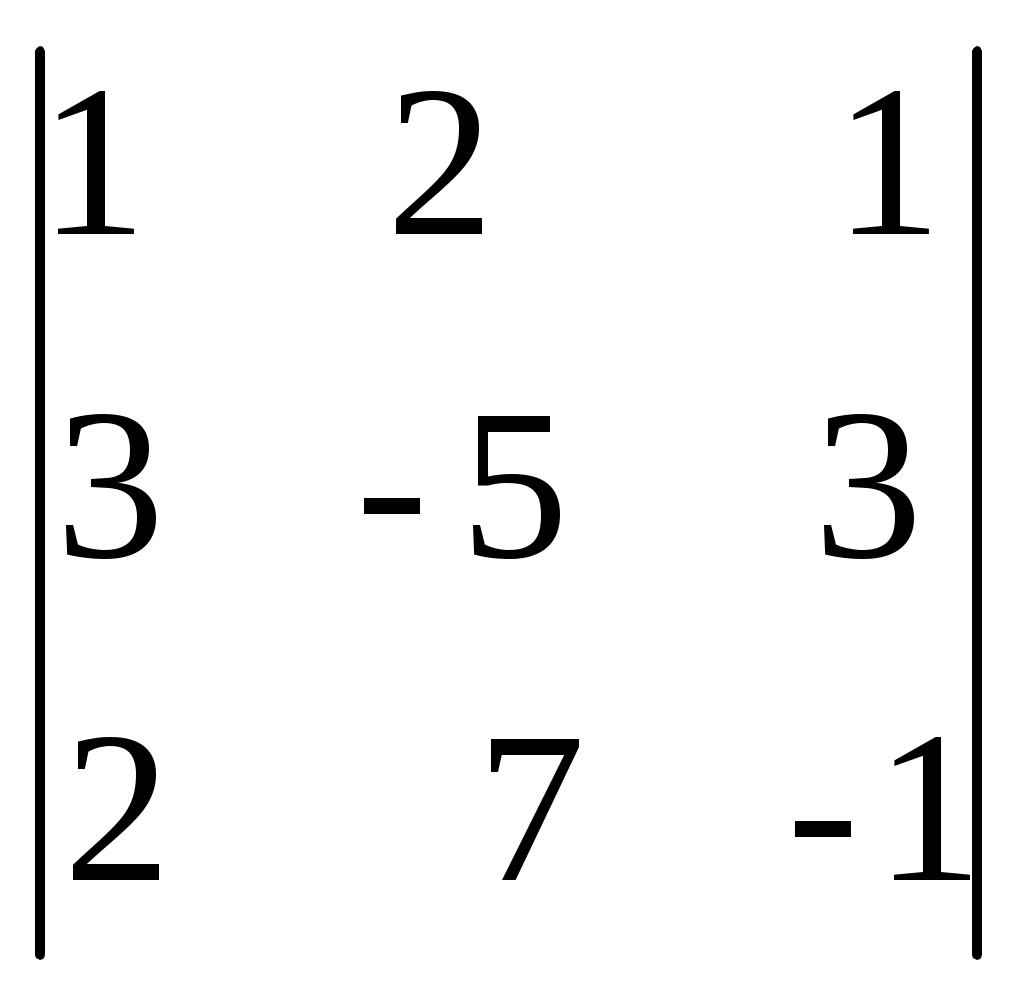

1) -23;

2)-33;

3)27;

4) 29;

5) 33.

5

Найти модуль вектора , если ,
1) 1;

2) 25;

3) 7;

4) 9

5) 5.