Тесты по математике 2курс1. Линейных уравнений называется совместной, если она
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
5 | | |||
| | Произведение | 1 | | |
| | Если векторы а и b перемножаются векторно, а их результат скалярно на вектор с, такое число называется… скалярным произведением; векторным произведением нулевым вектором смешанным произведением; общим решением . | 4 | | |
| | Какое произведение векторов обычно используют при нахождении углов между ними: Скалярное; векторное; смешанное; все 3 вида из пунктов 1,2,3; любое. | 1 | | |
| | Если векторы лежат на одной прямой или на параллельных прямых, то они называются… компланарными коллинеарными равными свободными ортогональными | 2 | | |
| | Если векторы лежат в одной плоскости или параллельны одной плоскости, то они называются … компланарными коллинеарными равными свободными ортогональными | 1 | | |
| | Два вектора коллинеарные, если… их соответствующие координаты равны их соответствующие координаты пропорциональны их смешанное произведение равно нулю их скалярное произведение равно нулю. Нет правильного ответа | 2 | | |
| | Два вектора ортогональны, если… их соответствующие координаты равны их соответствующие координаты пропорциональны их смешанное произведение равно нулю их скалярное произведение равно нулю. Нет правильного ответа | 4 | | |
| | Векторы компланарные, если … их соответствующие координаты равны их соответствующие координаты пропорциональны их смешанное произведение равно нулю их скалярное произведение равно нулю. Нет правильного ответа | 3 | | |
| | Модуль вектора 7 6 | 2 | | |
| | Какое произведение векторов приводит в итоге к новому вектору скалярное векторное смешанное все 3 вида из пунктов 1,2,3 любое | 2 | | |
| | Скалярное произведение вектора 2а на b , если -6 0 -2 2 6 | 5 | | |
| | Коллинеарные векторы – это векторы: лежащие на одной прямой. не лежащие на одной прямой. лежащие на параллельных прямых. верны 1) и 3). правильно 2) и 4). | 4 | | |
| | Косинус угла между векторами | 3 | | |
| | Скалярным произведением | 1 | | |
| | Найти длину вектора 5 25 7 1 12 | 1 | | |
| | Найти длину вектора 1) 36; 2) 6; 3) 4) 32; 5) | 2 | | |
| | Какие координаты имеет вектор (-3; -4; 12); (3; 4; 12); (-3; -4; -12); (3; 4; -12); нет верного ответа. | 4 | | |
| | Найти длину вектора 1) 12; 2) 1; 3) 11; 4) 7; 5) 0. | 4 | | |
| | Найти скалярное произведение векторов 1) –10; 2) 3; 3) -3; 4) 18; 5) –11. | 3 | | |
| | Найти скалярное произведение векторов 1) –1; 2) 1; 3) 0; 4) 7; 5) 14. | 3 | | |
| | (6,7) (6,-1) (2,-1) (3,5) (-2,7) | 2 | | |
| | (2,3) (10,15) (10,3) (2,15) (7,8) | 2 | | |
| | (-1;2) (7;6) (-12;8) (7;-2) (-1;6) | 5 | | |
| | (2;9) (-15;-9) (15;9) (2;0) (8;6) | 2 | | |
| | Даны вектора 1) 0; 2) 3; 3) 7; 4) 4; 5) -7. | 4 | | |
| | Чему равно смешанное произведение векторов 1) 29; 2) 33; 3) 7; 4) 0; 5) 1. | 1 | | |
| | Даны векторы | 1 | | |
| | Нулевым вектором называется вектор: Сумма координат которого равна нулю Произведение координат которого равна нулю Сумма координат которого равна единице Все координаты которого равны нулю Все координаты которого имеют равные знаки | 4 | | |
| | Найдите скалярное произведение векторов 3 13 (8;-5) (6;4) 21 | 1 | | |
| | Найти модуль вектора 14 6 -14 | 2 | | |
| | Найти скалярное произведение (с,d): с=(4;-2;-4), d=(6;-3;2) 1) (c,d)= 22 2) (c,d)=10 3) (c,d)=0 4) (с,d)=-c 5) (c,d)=-1 | 1 | | |
| | Даны векторы а=(2;-1;-2) и b=(8;-4;0) найти векторы с=2а и d=b-a 1) c=(5;-1;2), d=(4;1;2) 2) с=(4;-2;-4), d=(6;-3;2) 3) с=(0;0;1), d=(5;6;1) 4) с=(1;2;3), d=(2;0;1) 5) с=(2;3;1), d=(0;0;1) | 2 | | |
| | Вектор, у которого начало и конец совпадают, называется 1) нулевым и обозначается О 2) совпадающим 3) точкой вектором 4) равным 5) соответствующим | 1 | | |
| | Общее уравнение прямой на плоскости 1) Ах + Ву + С = 0; 2) 3) у = kx + b; 4) у – у1 = k (x – x1) ; 5) | 1 | | |
| | Уравнение прямой с угловым коэффициентом 1) Ах + Ву + С = 0; 2) 3) у = kx + b; 4) у – у1 = k (x – x1) ; 5) | 3 | | |
| | Уравнение прямой проходящей через данную точку в данном направлении 1) Ах + Ву + С = 0; 2) 3) у = kx + b; 4) у – у1 = k (x – x1) ; 5) | 4 | | |
| | Найти угол между векторами 1) 300; 2) 600; 3) 00; 4) 900; 5) 450. | 4 | | |
| | Уравнение прямой, проходящей через две данные точки 1) Ах + Ву + С = 0; 2) 3) у = kx + b; 4) у – у1 = k (x – x1) ; 5) | 2 | | |
| | Формула расстояния между точками 1) d x 2) d 3) d 4) d 5) d | 5 | | |
| | Найти расстояние от точки -3 4 до оси Ох 1) -3 2) 4 3) 25 4) 7 5) 1 | 2 | | |
| | Чему равен радиус окружности х2-6х+у2=0 1) 2; 2) 4; 3) 3; 4) 5; 5) 6. | 3 | | |
| | Чему равна малая полуось эллипса х2+4у2=16 1) 2; 2) 4; 3) 6; 4) 8; 5) 10. | 1 | | |
| | Чему равно расстояние между вершинами гиперболы х2- 4у2=16 1) 6; 2) 4; 3) 10; 4) 8; 5) 16. | 2 | | |
| | Какое произведение векторов обычно используют при вычислении площади параллелограмма: 1) Скалярное; 2) Векторное; 3) Смешанное; 4) все 3 вида из пунктов 1,2,3; 5) любое. | 2 | | |
| | Какое произведение векторов обычно используют при вычислении площади треугольника: 1) Скалярное; 2) Векторное; 3) Смешанное; 4) все 3 вида из пунктов 1,2,3; 5) любое. | 2 | | |
| | Какое произведение векторов обычно используют при нахождении углов между ними: 1) Скалярное; 2) Векторное; 3) Смешанное; 4) все 3 вида из пунктов 1,2,3; 5) любое. | 1 | | |
| | Найти расстояние от начало координат до прямой 2х-5=0 1) 2 2) 5 3) 5/2 4) -5/2 5) -2 | 3 | | |
| | Какое произведение векторов обычно используется при нахождении объема пирамиды 1) скалярное 2) векторное 3) смешанное; 4) все 3 вида из пунктов 1,2,3; 5) любое. | 3 | | |
| | Какое произведение векторов обычно используется при нахождении объема параллелепипеда 1) скалярное 2) векторное 3) смешанное; 4) все 3 вида из пунктов 1,2,3; 5) любое. | 3 | | |
| | Найти уравнение асимптот гиперболы 1) у= 2) у= 3) у= 4) у= 5) у= | 1 | | |
| | Найти эксцентриситет гиперболы 4/3 -4/3 5/3 | 5 | | |
| | Найти координаты фокусов F1 и F2 гиперболы 1)(5,0), (0,5) 2)(5,0), (-5,0) 3)(4,0), (-4,0) 4)(3,-1), (0,2) 5)(0,-2), (0,-2) | 2 | | |
| | Определить тип кривой второго порядка х2 + у2 – 4х + 6у + 4 = 0 1) эллипс 2) окружность 3) гипербола 4) парабола 5) прямая | 2 | | |
| | Определить тип кривой второго порядка 2х2 + 5у2 +8х -10у -17 = 0 1) эллипс 2) окружность 3) гипербола 4) парабола 5) прямая | 1 | | |
| | Уравнение асимптот для гиперболы х2-у2=3 имеет вид 1) у= 2) у=3х 3) у=3 4) х=3 5) у=0 | 1 | | |
| | Определить тип кривой второго порядка х2 -6у2 -12х +36у -48 = 0 1) эллипс 2) окружность 3) гипербола 4) парабола 5) прямая | 3 | | |
| | Написать уравнение прямой, которая проходит через точку А (3,-1) и параллельна оси ординат: 1)х=3 2)х=5 3)х=8 4)х=1 5)х=2 | 1 | | |
| | Написать уравнение прямой, проходящей через начало координат и через точку (-2,3) 1)у=1,5х 2)у=-1,5х 3)у=2х/3 4)у=3х 5)у=-3х | 2 | | |
| | Среди прямых l1 с уравнением 3х-2у+7=0, l2 с уравнением 6х-4у-9=0 и l3 с уравнением 6х+4у-5=0 указать параллельные: 1) l1 l3 2) l2 l3 3) l1 l2 4) нет -ых 5) нет правильного ответа | 3 | | |
| | Среди прямых l1 с уравнением 6х-4у-5=0, l2 с уравнением 2х+3у-6=0 и l3 с уравнением 4х-у-7=0 указать перпендикулярные: 1)нет -ых 2)l1l3 3)l2l3 4)l1l2 5)нет правильного ответа | 4 | | |
| | Найти координаты центра окружности х2-10х+у2=0 1) (5,0) 2) (2,0) 3) (1,1) 4) (10,1) 5) (-2,0) | 1 | | |
| | Найти координаты центра окружности х2-6х+у2-9=0 1) (1,0) 2) (2,0) 3) (3,0) 4) (6,1) 5) (6,9) | 3 | | |
| | Найти расстояние от точки А (1,1) до точки В(4,5): 1) 2 2) 3 3) 4 4) 5 5) 6 | 4 | | |
| | Геометрическое место точек, разность расстояний каждой из которой от двух данных точек F1 и F2, есть постоянная величина, называется 1) окружностью 2) эллипсом 3) гиперболой 4) параболой 5) кривой второго порядка | 3 | | |
| | Какая из приведенных ниже точек лежит на окружности х2 + у2 – 2х – 3 = 0 1) (0,0) 2) (-1,0) 3) (1,0) 4) (0,1) 5) (-1,2) | 2 | | |
| | Дано уравнение линии 1) Эллипс; 2) Парабола; 3) Гипербола; 4) Окружность; 5) Спираль Архимеда; | 3 | | |
| | Даны векторы 1) 21 2) 19 3) 18 4) -12 5) 15 | 3 | | |
| | Определить координаты вектора -3b, если вектор b(-1/3;-1/5) 1) (-1;-3/5) 2) (1;3/5) 3) (-1/6;-1/8) 4) (1/6;-1/8) 5) (1/9;3/5) | 2 | | |
| | Найти разность векторов a(-5;2) и b(10;-4) 1) (15;6) 2) (5;-2) 3) (-15;6) 4) (-5;-2) 5) (2;-5) | 3 | | |
| | Укажите уравнение окружности с диаметром 12, и центр лежит в начале координат 1) 6x2 + 6y2 = 3 2) x2 + y2 = 3 3) x2 + y2 = 9 4) 5x2 + 5y2 = 9 5) x2 + y2 = 36 | 5 | | |
| | Определить косинус угла между векторами a (1; 2; 3) и b (6; 4; -2) 1) 3 2) 4/7 3) 0 4) 5 5) 2/7 | 5 | | |
| | Укажите уравнение окружности с диаметром 6, и центр лежит в начале координат 1) 6x2 + 6y2 = 3 2) x2 + y2 = 3 3) x2 + y2 = 9 4) 5x2 + 5y2 = 9 5) x2 + y2 = 36 | 3 | | |
| | Формула координаты середины отрезка: 1) x= 2) x= 3) x= 4) x= 5) нет верного ответа. | 1 | | |
| | Даны точки А(2;3;-1) и В (0;1;4). Найдите координаты вектора (2;2;-5) (-2;-2;5) (2;4;3) (2;2;3) (1;3;-1) | 2 | | |
| | Найти точку пересечением прямых 3x-y-2=0 и 2x+y-3=0: (1;-1) (-1;1) (1;1) (1;0) (-1;2) | 3 | | |
| | Найти длину вектора 9 5 0 1 8 | 2 | | |
| | Условие параллельности двух прямых y= k1x+ в1 и y=k2x+в2: | 3 | | |
| | Компланарными векторами называются: Три вектора, лежащие на одной прямой или параллельных прямых. Три вектора, лежащие на одной прямой Три вектора, лежащие на одной плоскости. Три вектора, образующие треугольник. Три вектора, лежащие на одной плоскости или на параллельных плоскостях. | 5 | | |
| | Угловой коэффициент прямой -10х + 2у + 8 = 0 равен: 3 5 -5 10 2 | 2 | | |
| | Ах+Ву+С=0. В каком виде задано уравнение прямой: в отрезках в общем виде проходящая через две данные точки с угловым коэффициентом правильный ответ не указан. | 2 | | |
| | Условие перпендикулярности двух прямых | 4 | | |
| | Условие перпендикулярности прямых 1) 2) 3) 4) - 5) - | 3 | | |
| | Уравнение эллипса: 1) 2) 3) 4) x 5) | 5 | | |
| | Уравнение гиперболы: 1) 2) 3) 4) x 5) | 1 | | |
| | Определить расстояние между точками А (3,8) и В (-5, 14): 1) 5. 2) 10. 3) 4)-10. 5) 13. | 2 | | |
| | Какая прямая параллельна прямой у=-3х+5? 1) у = 3 х-5. 2)у=3х+1. 3)у= 4) у = - 3 х + 8. 5) у =- | 4 | | |
| | Найдите скалярное произведение векторов а(4,-1),вектор b(2;5): 1) 3 2) 13 3) (8; - 5) 4) (6; 4) 5)21 | 1 | | |
| | Составить уравнение прямой, имеющий угловой коэффициент k = 2 и проходящей через точку М (-5 ; 3 ): 1) х+2у-13=0 2) х-2у-13=0 3) х-2у+13=0 4) 2х-у+13=0 5) 2х + у - 13=0 | 4 | | |
| | Векторы а и в называются равными, если 1) они коллинеарные, одинаковы направлены и их длины равны 2) они компланарны 3) они пересекаются 4) они имеют противоположные знаки 5) лежат в разных плоскостях | 1 | | |
| | Векторы а и в называются коллинеарными, если 1) они лежат на одной прямой или на параллельных прямых 2) они лежат в противоположным направлении 3) они лежат на перпендикулярных плоскостях 4) они равны 5) они равны по абсолютной длине и противоположны по направлению | 1 | | |
| | Направленный отрезок называется вектором диагональю линией кривой касательной | 1 | | |
| Укажите на ложное утверждение: 1)Для того, чтобы система линейных неоднородных уравнений была совместной, необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу расширенной матрицы; 2)Если определитель основной матрицы системы линейных однородных уравнений равен нулю, то система имеет ненулевых решений; 3)Если определитель основной матрицы системы линейных неоднородных уравнений равен нулю, то он имеет бесконечное множество решений; 4)Если ранг r основной матрицы совместной системы линейных неоднородных уравнений меньше числа неизвестных n, то система имеет бесконечное множество решений; 5)Если ранг r основной матрицы системы линейных однородных уравнений равен числу неизвестных n, то система имеет ненулевые решения. | 5 | |||
| Вычислить определитель Δ =  1)12; 2)-12; 3) 6; 4) 2; 5) 16 | 1 | |||
| Вычислить определитель: 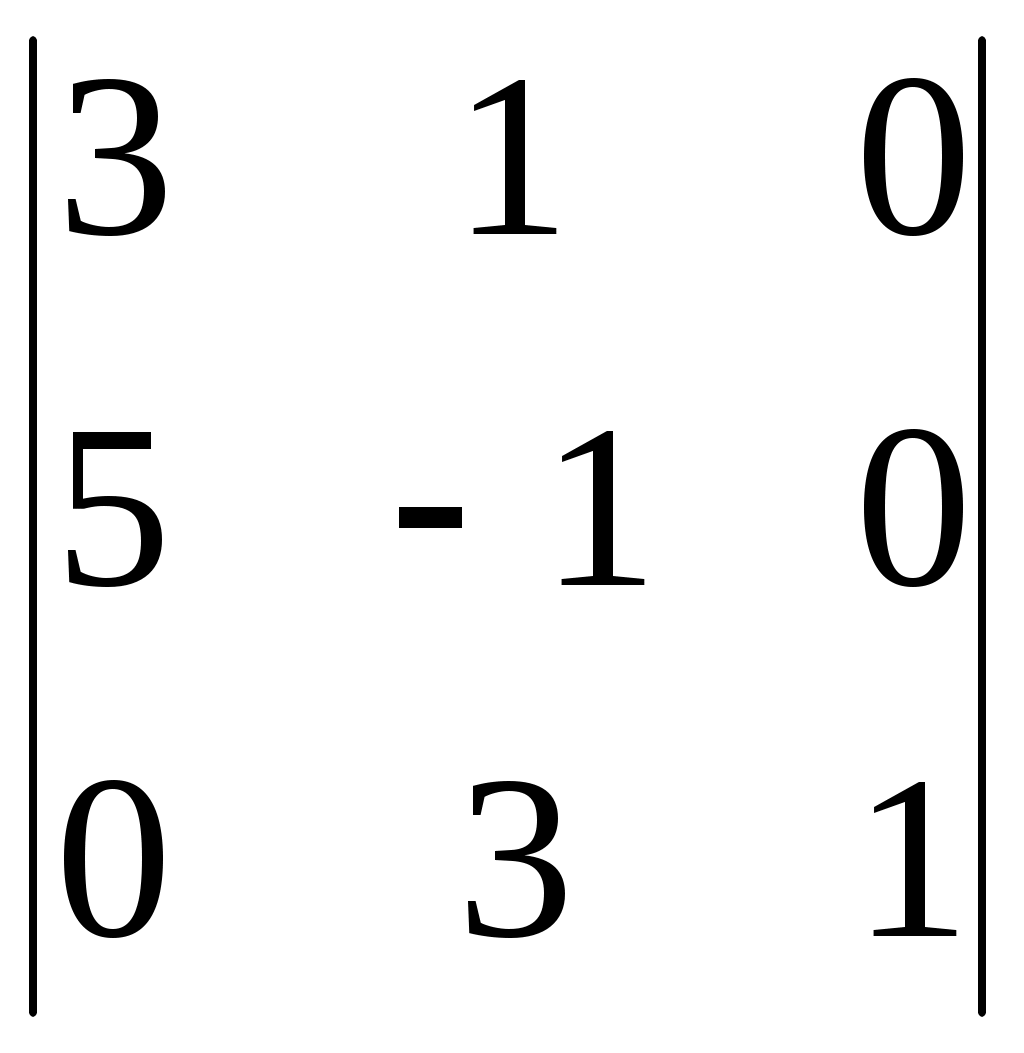 24 40 -8 -16 14 | 3 | |||
| В каких случаях применяется метод Крамера решения совместной системы неоднородных линейных уравнений? 1)Если определитель основной матрицы отличен от нуля; 2)Если ранг r основной матрицы не равен числу неизвестных n (rn); 3)Если rn; 4)Если rn. 5)Если число линейно независимых строк основной матрицы равен рангу расширенной матрицы. | 1 | |||
| Вычислите алгебраическое дополнение А32 элемента а32 определителя =  1)13; 2)4; 3)– 4; 4)6; 5)0; | 3 | |||
| Из матричного уравнения | 1 | |||
| 1) 2) 3) 4) 5) | 3 | |||
