Тесты по математике 2курс1. Линейных уравнений называется совместной, если она
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
5 | ||||
| Вычислить определитель 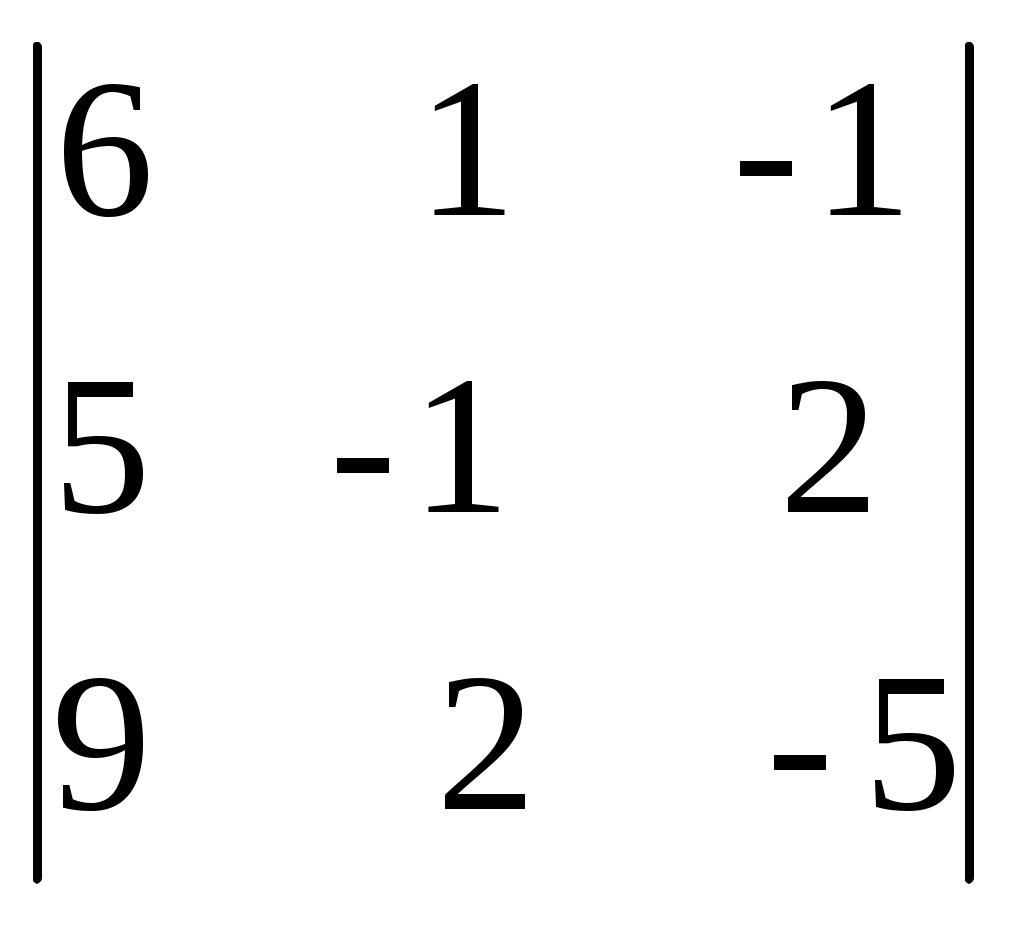 : :1) -15; 2) 30; 3) 15 ; 4) -30; 5) 0 . | 2 | |||
| Вычислить определитель 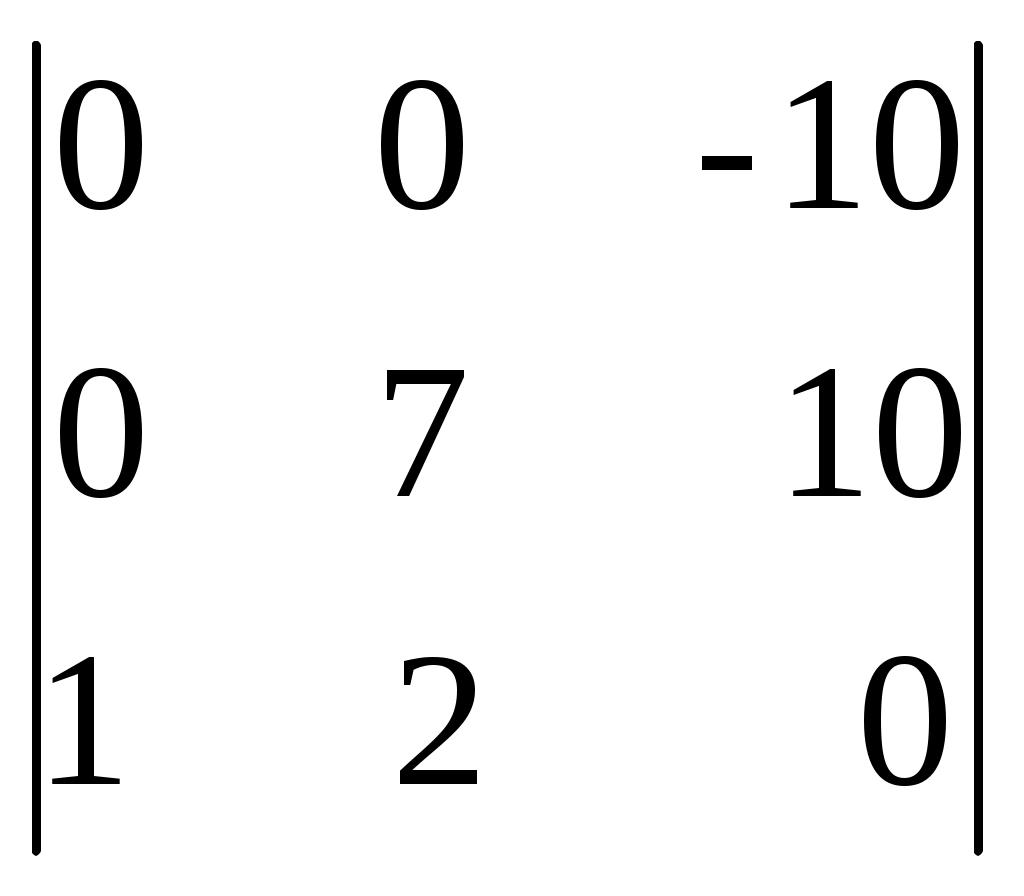 : :1) 25; 2) 70; 3) 80; 4) 50; 5) -70 | 2 | |||
| Вычислить определитель 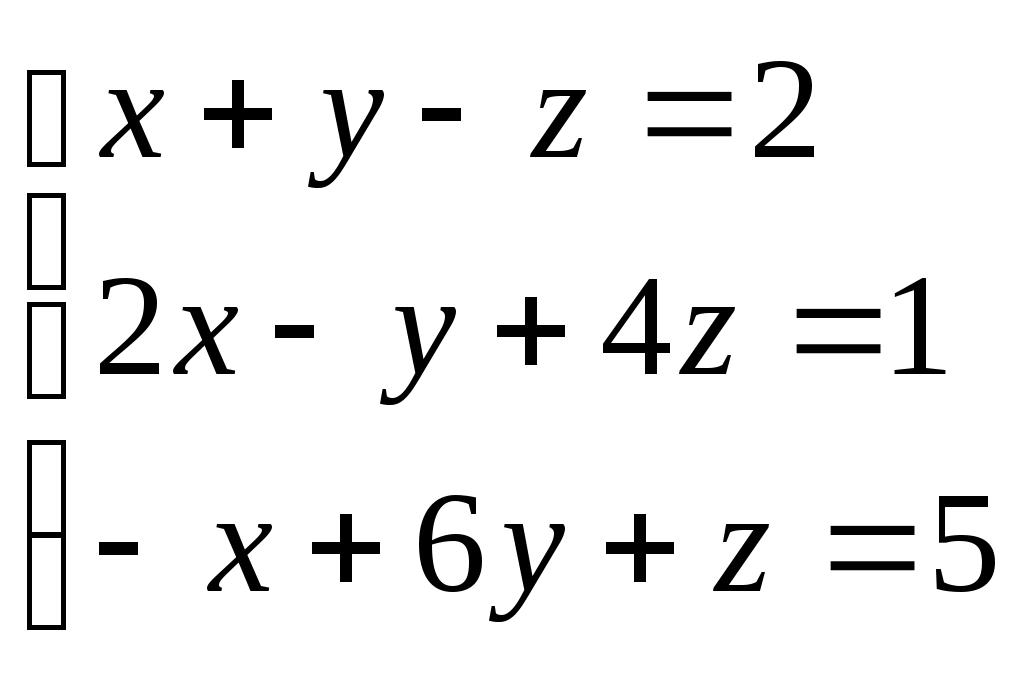 1) 2) 3) 4) 5) | 2 | |||
| Какую матрицу прибавить к матрице А, чтобы получить единичную матрицу А= 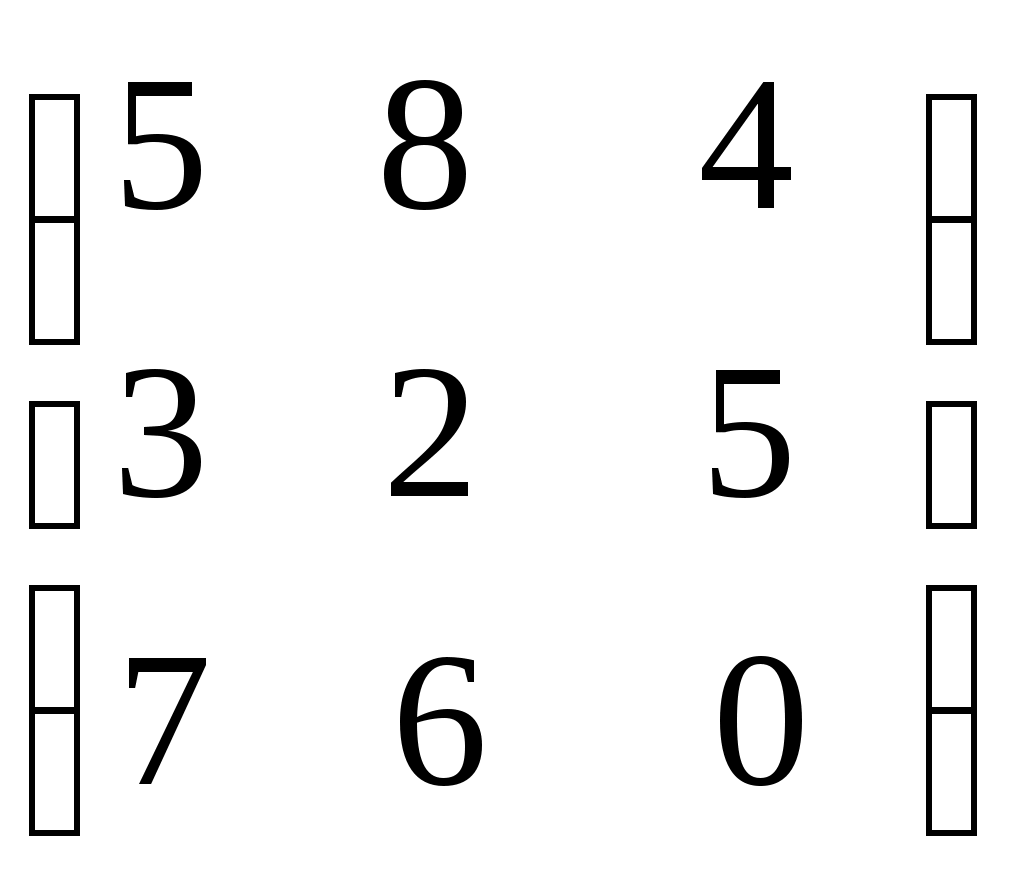 1) 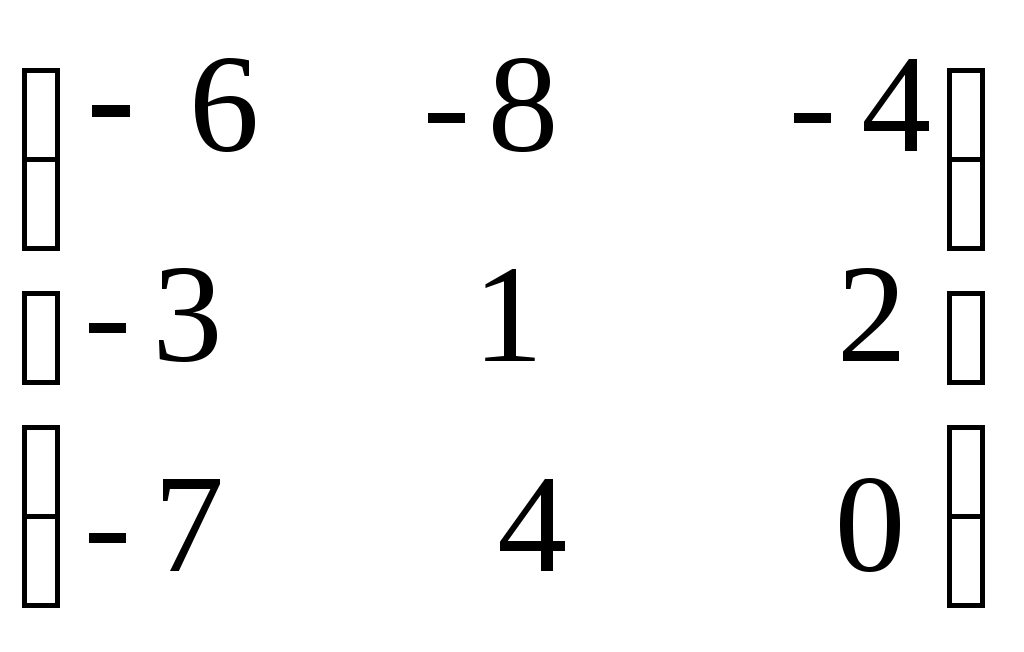 ; ;2) 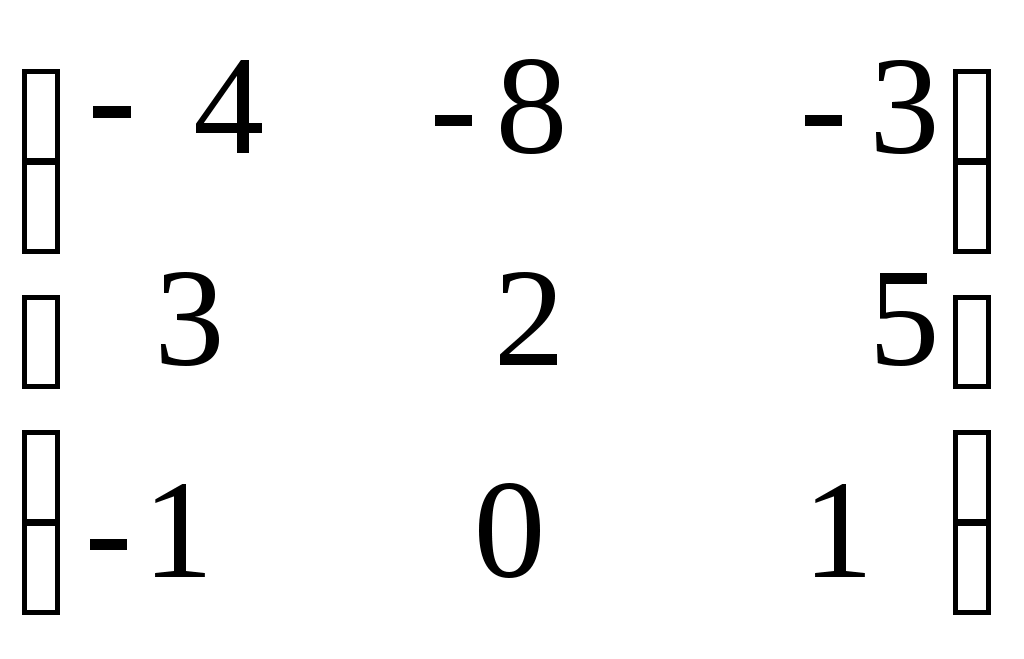 ; ;3) 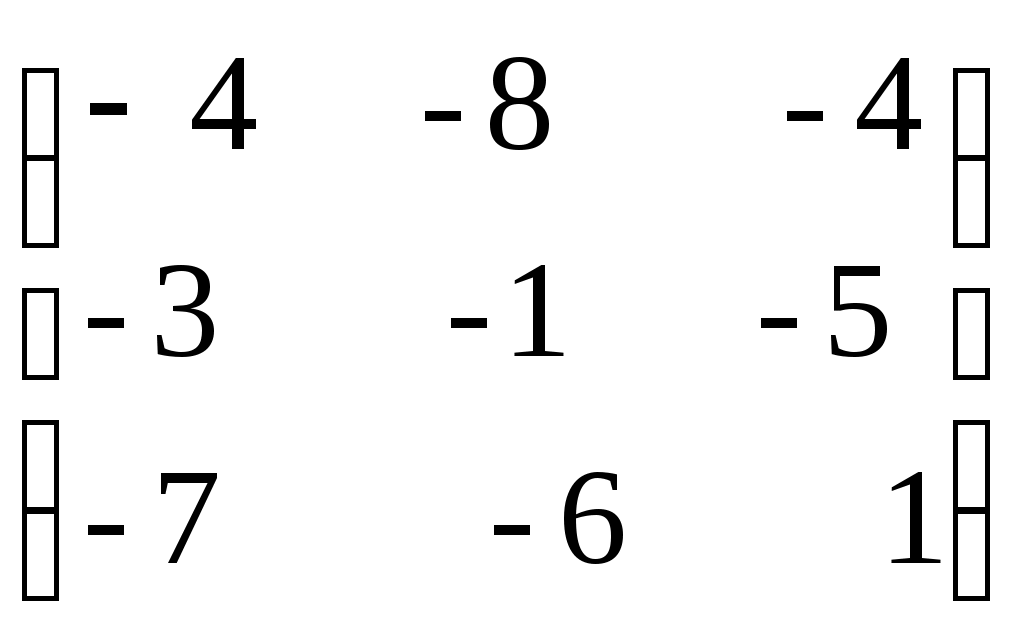 ; ;4) 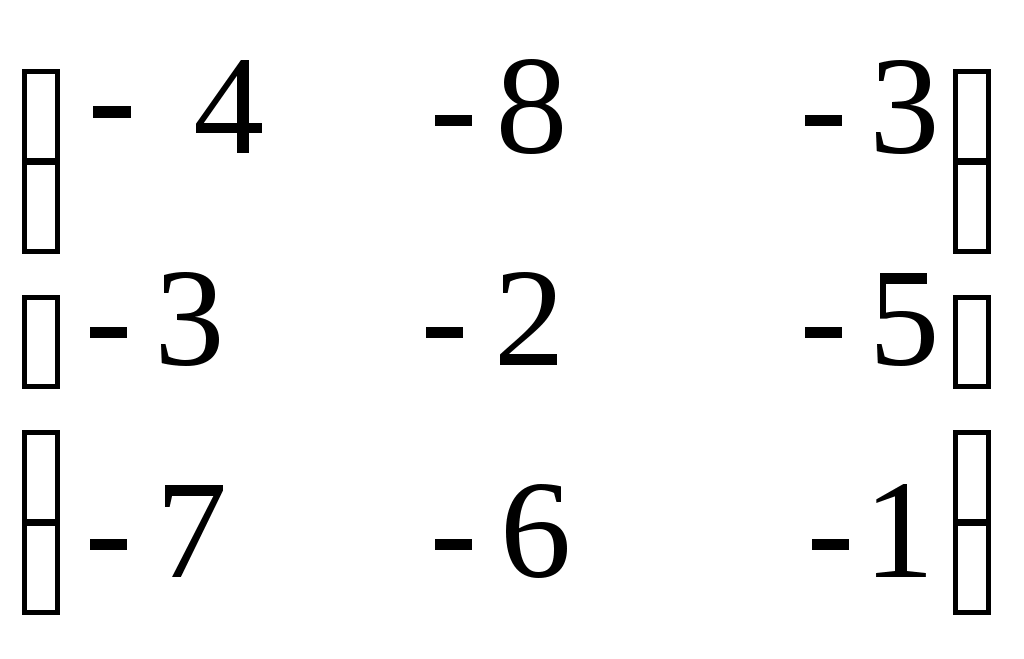 ; ;5) 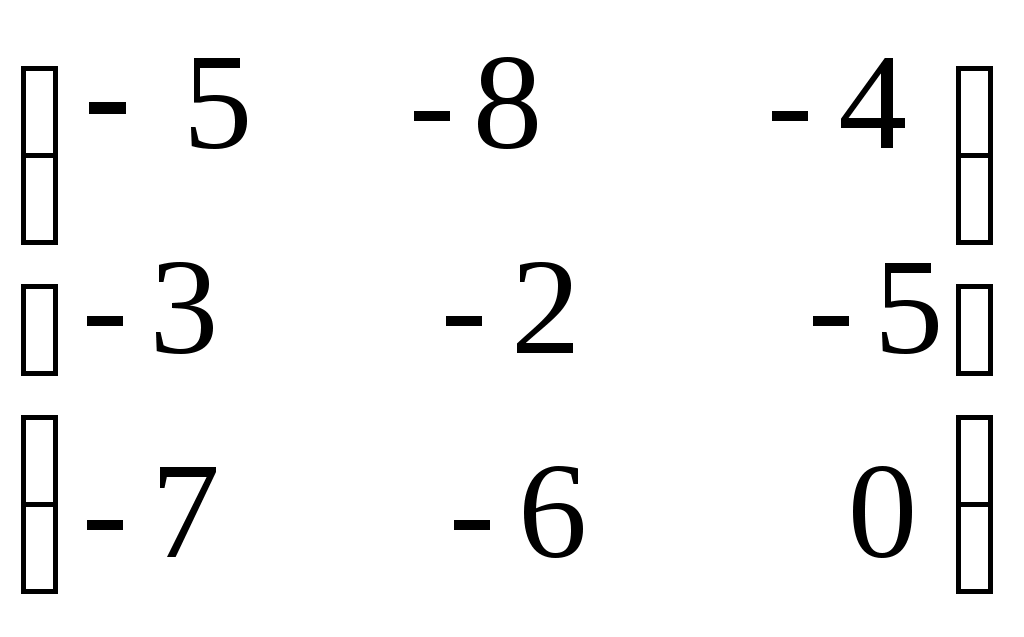 . . | 3 | |||
| Квадратная матрица, у которой все элементы кроме элементов главной диагонали равны нулю, называется 1) Единичной 2) Треугольной; 3) Диагональной; 4) Транспонированной; 5) Нулевой. | 3 | |||
| Матрица, полученная из данной заменой каждой её строки столбцом с тем же номером, называется: 1) Единичной; 2) Треугольной; 3) Диагональной; 4) Транспонированной; 5) Квадратной. | 4 | |||
Произведение | 1 | |||
| Если векторы а и b перемножаются векторно, а их результат скалярно на вектор с, такое число называется… 1) Скалярным произведением; 2) Векторным произведением 3) Нулевым вектором 4) Смешанным произведением; 5) Общим решением. | 4 | |||
| Найти угол между прямыми х-у-4=0, 2х+2у-5=0 1) 900; 2) 150; 3) 450; 4) 600; 5) 00. | 5 | |||
| Уравнение асимптот для гиперболы х2-у2=2 имеет вид: 1) у=2; 2) у=х; 3) у=2х; 4) у=0; 5) х=2 . | 2 | |||
| Уравнение асимптот для гиперболы х2-у2=1 имеет вид: 1) у=х; 2) у=1; 3) х=1; 4) у=0; 5) х=0. | 1 | |||
| Уравнение асимптот для гиперболы х2-у2=22 имеет вид: 1) у=2 2) у=х; 3) х=2; 4) у=2х; 5) у=0. | 2 | |||
| Чему равен радиус окружности х2-6х+у2=0 1) 2; 2) 4; 3) 3; 4) 5; 5) 6. | 3 | |||
| Чему равна малая полуось эллипса х2+4у2=16 1) 2; 2) 4; 3) 6; 4) 8; 5) 10. | 1 | |||
| Чему равно расстояние между вершинами гиперболы х2- 4у2=16 1) 6; 2) 4; 3) 10; 4) 8; 5) 16. | 4 | |||
| Уравнение 1) Эллипсоид; 2) Однополостный гиперболоид; 3) Двуполостный гиперболоид; 4) Конус второго порядка; 5) Эллиптический параболоид. | 1 | |||
| Уравнение 1) Эллипсоид; 2) Однополостный гиперболоид; 3) двуполостный гиперболоид; 4) конусы второго порядка; 5) эллиптические параболоиды. | 2 | |||
| Уравнение 1) Эллипсоид; 2) Однополостный гиперболоид; 3) Двуполостный гиперболоид; 4) Конус второго порядка; 5) Эллиптический параболоид. | 3 | |||
| Уравнение 1) Эллипсоид; 2) Однополостный гиперболоид; 3) Двуполостный гиперболоид; 4) Конус второго порядка; 5) Эллиптический параболоид. | 4 | |||
| Уравнение 1) Эллипсоид; 2) Однополостный гиперболоид; 3) Двуполостный гиперболоид; 4) Конус второго порядка; 5) Эллиптический параболоид. | 5 | |||
| Уравнение 1) Гиперболические параболоиды; 2) Эллиптические цилиндры; 3) Гиперболические цилиндры; 4) Параболические цилиндры; 5) Эллипсоиды. | 1 | |||
| Уравнение 1) Гиперболические параболоиды; 2) Эллиптические цилиндры; 3) Гиперболические цилиндры; 4) Параболические цилиндры; 5) Эллипсоиды. | 2 | |||
| Уравнение 1) Гиперболические параболоиды; 2) Эллиптические цилиндры; 3) Гиперболические цилиндры; 4) Параболические цилиндры; 5) Эллипсоиды. | 4 | |||
| Какое произведение векторов обычно используют при вычислении площади параллелограмма: 1) Скалярное; 2) Векторное; 3) Смешанное; 4) все 3 вида из пунктов 1,2,3; 5) любое. | 2 | |||
| Какое произведение векторов обычно используют при вычислении площади треугольника: 1) Скалярное; 2) Векторное; 3) Смешанное; 4) все 3 вида из пунктов 1,2,3; 5) любое. | 2 | |||
| Какое произведение векторов обычно используют при нахождении углов между ними: 1) Скалярное; 2) Векторное; 3) Смешанное; 4) все 3 вида из пунктов 1,2,3; 5) любое. | 1 | |||
| Прямая l имеет уравнение Ах+С=0, где А 1)lОу; 2)lО(0,0); 3)lне Ох; 4) lОх; 5) lне Оу;. | 1 | |||
| Прямая l имеет уравнение Ву+С=0, где В 1)lОу; 2)lО(0,0); 3)lне Ох; 4) lОу; 5) lне Оу;. | 4 | |||
| Прямая l имеет уравнение Ах+Ву+С=0, где А 1)lне О(0,0); 2) l Ох; 3)l Оу; 4) lОх; 5) l О(0,0); | 1 | |||
| Прямая l имеет уравнение х=а0, тогда: 1)lне О(0,0); 2) l Ох; 3)l Оу; 4) l неОх; 5) l О(0,0). | 3 | |||
| Прямая l имеет уравнение у=b0, тогда: 1)lне О(0,0); 2) l Ох; 3)l Оу; 4) lнеОy; 5) l О(0,0). | 2 | |||
| Прямая l имеет уравнение у=kx, где k0, тогда 1)lне О(0,0); 2) l Ох; 3)l Оу; 4) lОх; 5) l О(0,0). | 5 | |||
| Прямая l имеет уравнение у=kx+b, где k0, b0, тогда 1)lне О(0,0); 2) l Ох; 3)l Оу; 4) lОх; 5) l О(0,0); | 1 | |||
| Решить систему уравнений 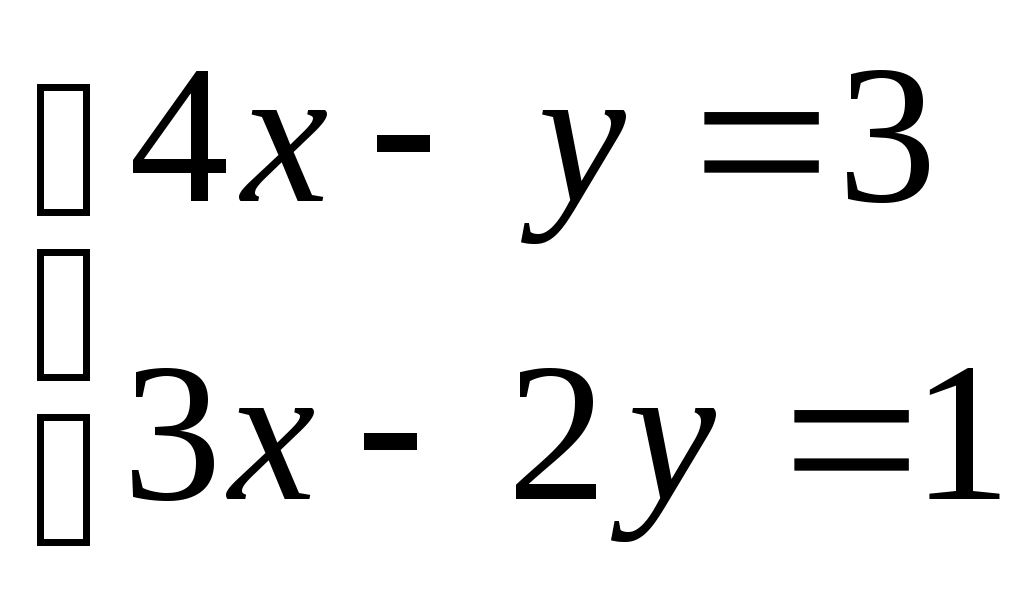 1) х=у=-1; 2) х=2, у=1; 3) х=у=1; 4) х=0, у=1; 5) х=1, у=-1 | 3 | |||
| Решить систему уравнений 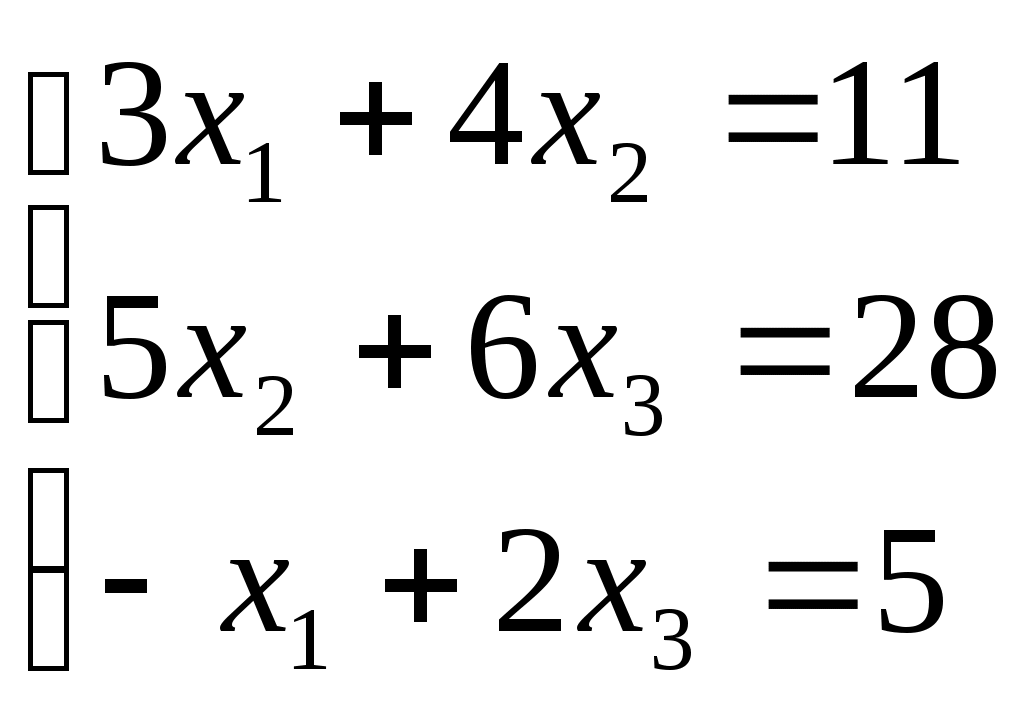 : :1) (1,2,3); 2) (-1,-2,3); 3) (1,-3,-2); 4) (-1,-2,-3); 5) (1,2,-3). | 1 | |||
| Решить систему уравнений 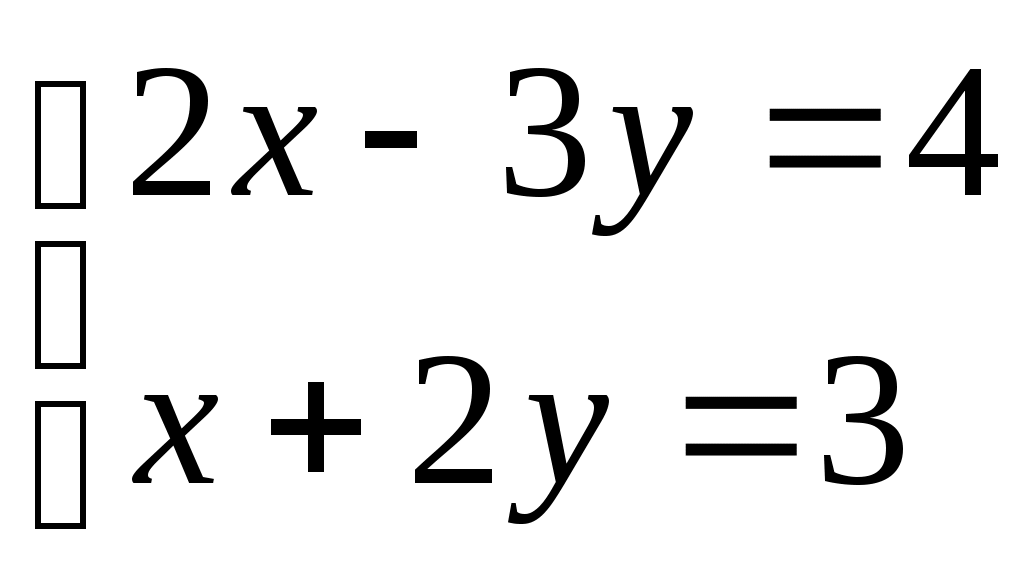 1) х=2/7, у=17/7; 2) х=-2/7, у=-17/7; 3) х=17/7, у=-2/7 4) не имеет решения; 5) х=17/7, у=2/7. | 5 | |||
| Найти расстояние от начало координат до прямой 2х-5=0 1) 2 2) 5 3) 5/2 4)-5/2 5)-2 | 3 | |||
| Какое произведение векторов обычно используется при нахождении объема пирамиды 1) скалярное 2) векторное 3) смешанное; 4) все 3 вида из пунктов 1,2,3; 5) любое. | 3 | |||
| Какое произведение векторов обычно используется при нахождении объема параллелепипеда 1) скалярное 2) векторное 3) смешанное; 4) все 3 вида из пунктов 1,2,3; 5) любое. | 3 | |||
| Для точки М(х,у) справедливы формулы 1) полярные координаты точки М через её прямоугольные координаты; 2) прямоугольные координаты точки М через полярные; 3) расстояние между х и у; 4) полярный радиус; 5) полярный угол. | 1 | |||
| Прямоугольные координаты точки М через её полярные координаты выражаются в форме 1) х= , у =cos; 2) х=1, у =; 3) х=у, у= sin 4) x= cos, y=sin; 5) x= arcsin, y=. | 4 | |||
| Каждой точке плоскости соответствует: 1) две пары действительных чисел х1,х2,у1,у2; 2) одна пара действительных чисел х и у; 3) одно действительное число 4) пара комплексных чисел 5) одно число определяемой у. | 2 | |||
| Совокупность координатных осей Ох, Оу и выбранной единицы масштаба называют 1) полярной системой координат; 2) евклидовой системой координат; 3) декартовой системой координат; 4) «n»-мерной системой координат; 5) осевой системой координат. | 3 | |||
| Написать уравнение прямой проходящей через точки А(-1,2,3) и В(2,6,-2) A) | ||||
